Сообщества живых организмов похожи на фракталы

Фракталы выглядят завораживающе – в этом их несомненное сходство с живыми объектами (изображение с сайта http://upload.wikimedia.org).

До середины прошлого века в математике и естественных науках в целом господствовал «аналитический» подход, когда все объекты представляются простыми математическими абстракциями типа гладкой линии, конуса, шара, поверхности... С течением времени ученые столкнулись с необходимостью описания множества сильно разнородных объектов, втиснуть которые в «аналитическую» парадигму оказалось очень непростой задачей. На этой основе был разработан альтернативный – фрактальный -– подход. Создателем этого подхода является Бенуа Мандельброт (редчайший в современной науке случай, когда создание целого обширнейшего направления можно связать с именем одного ученого), а выход его книги «Фрактальная геометрия природы» в 1982 году можно считать знаковой для науки конца прошлого века датой. Именно после выхода этой книги «открылись глаза» у огромного числа исследователей из самых различных отраслей наук. Начался своего рода фрактальный бум, продолжающийся до сих пор...

Со временем фрактальная идеология стала проникать и в экологию. Первые ее применения связаны с описанием пространственной сложности тех или иных биотопов. Выяснилось, что фрактальной структурой обладают горы, долины, речные системы, почва, рифы... Фрактальная геометрия оказалась удобным инструментом для описания биотопов.

Затем встал вопрос о фрактальности распределения отдельных видов. Суть фрактальной модели сводится к тому, что агрегированность особей принимается статистически однородной при различных масштабах рассмотрения. Например, ареал вида разбивается на несколько участков обитания, те, в свою очередь, состоят из ряда более мелких местообитаний, в пределах которых выделяются скопления особей и т.д. Это чисто геометрическая модель, совершенно естественно и наглядно демонстрирующая фрактальность и самоподобие. Впервые она появилась в начале 1990-х годов в контексте дискуссии об описании территориальных участков животных. В конце того же десятилетия появились попытки применения фрактальной модели на уровне, сопоставимом с ареалами отдельных видов. В частности, подробному анализу подверглись атласы флоры Великобритании, Голландии, атлас распространения птиц центральной Европы. Применение фрактальной модели дало обнадеживающие результаты.

Логичным продолжением этой линии «фрактализации» экологии стало появление представлений о фрактальности и самоподобии фундаментального объекта экологии – биологического сообщества. При этом довольно быстро выяснилось, что экологи на протяжении уже примерно столетия использовали элементы математического аппарата, используемого фрактальной геометрией. В частности, свойство самоподобия фрактального объекта проявляется в виде степенной зависимости числа структурных элементов от масштаба. Применительно к биологическому сообществу элементарными «кирпичиками», его составляющими, будут отдельные виды. А в качестве масштаба естественным образом можно рассматривать площадь. Зависимость видового богатства (числа составляющих сообщество видов) от площади – одна из самых обсуждаемых проблем экологии на протяжении всей ее (экологии) истории. И самой распространенной математической моделью для описания этой зависимости является именно степенной закон. Один этот факт дает основание считать биологическое сообщество фракталом, а показатель, характеризующий скорость накопления видового богатства при росте площади, – фрактальной размерностью. В явном виде эта идея была озвучена в 1999 году группой американских исследователей, возглавляемой Джоном Харте.

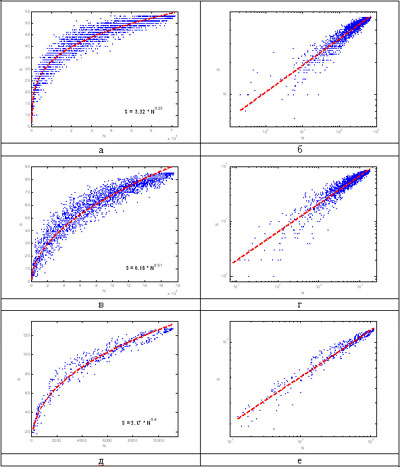
Графики накопления видового богатства в натуральных (а, в, д) и билогарифмических (б, г, е) координатах. По горизонтальной оси — число особей в выборке. По вертикальной оси — число попавших в выборку видов. а, б — зоопланктоценозы (сообщества планктонных животных) Чебоксарского водохранилища. в, г — зообентоценозы (сообщества донных животных) малых озер г. Нижнего Новгорода. д, е — сообщества почвенных клещей г. Нижнего Новгорода

В дальнейшем выяснилось, что самоподобие структуры биологического сообщества может проявляться не только в его пространственном распределении. Дело в том, что проблема накопления видового богатства имеет и непространственный аспект. В практическом плане наиболее распространенным способом получения эмпирических данных является выборочный метод. Он подразумевает изъятие выборок из того или иного изучаемого сообщества с целью получения информации о его видовом составе, видовой структуре, разнообразии и других характеристиках. Использование выборочного метода сопряжено с множеством серьезных проблем при интерпретации материала: какова репрезентативность полученных выборок; каков должен быть объем выборки (или, что то же, сколько проб необходимо отобрать) для адекватной характеристики структуры сообщества; как сравнивать между собой выборки различного размера? Одним из подходов к разрешению такого рода проблем служит использование так называемых кривых накопления видов. Кривая накопления видов строится как зависимость видового богатства от накопленного выборочного усилия (это может быть число отобранных особей, число отработанных ловушкосуток, объем процеженной воды и т.д.). Выборочное усилие в этом случае можно считать мерой масштаба, и тогда кривая накопления видов становится аналогом зависимости видового богатства от площади. Если она также описывается степенным законом, то и в непространственном аспекте можно говорить о самоподобии и фрактальности структуры биологического сообщества.

И действительно, степенная зависимость применяется для формализации кривых накопления видов. А один из крупнейших экологов ушедшего века Рамон Маргалеф в явном виде отождествил показатель степени, описывающий зависимость числа видов от числа особей, с фрактальной размерностью.

В качестве иллюстрации этого положения в статье рассмотрен характер накопления видового богатства от числа особей для гидробиоценозов (на основе данных по зоопланктону Чебоксарского водохранилища и макрозообентосу городских озер Нижнего Новгорода) и наземного сообщества (на основе данных по группе орибатидных клещей парков Нижнего Новгорода и окрестностей).

См. также: Распределение организмов по морскому дну проявляет фрактальные свойства