Посчитанные отражения

Теория групп, разработанная в математике для формального описания симметрии математических объектов, позволяет выразить количественно также и симметрию объектов биологических, таких как цветы. Учитывая разные признаки, такие как размер и число лепестков, их цвет и т. д., можно сравнивать по единому алгоритму степень симметричности внешне непохожих организмов. Разработанные компьютерные программы помогают не только автоматизировать процесс, но и провести сравнение объектов с любой степенью подробности.

Симметрия повсеместно наблюдается в живой природе, однако биологические объекты, как правило, не идеально, а лишь приблизительно симметричны. Их еще называют «псевдосимметричными». Тем не менее, тип симметрии характеризует живой объект наряду с другими морфологическими, физиологическими, генетическими и прочими признаками, благодаря которым мы отличаем одни организмы от других.

В работе сотрудников Нижегородского государственного университета им. Н.И. Лобачевского излагаются основные положения теории групп, позволяющей количественно оценить симметрию биологических объектов (кстати, недавно в серии «Элементы» вышла научно-популярная книга Иэна Стюарта «Истина и красота», посвященная теории групп). Авторы предлагают метод, который дает возможность сравнения между собой объектов разной степени симметрии.

Традиционно биологи обсуждают симметрию в терминах описательного свойства, не позволяющих оценить симметрию количественно. Хотя, конечно, число преобразований объекта, при которых он остается тождественным самому себе: количество точек, осей и плоскостей симметрии, – вполне поддаётся счёту. Такие точки, оси и плоскости называются элементами симметрии.

Во многих случаях симметричные преобразования объекта отнюдь не произвольны, а составляют строго определенные сочетания, называемые точечными группами. В статье перечислены условия, при которых набор геометрических преобразований будет являться именно группой.

Например, 5-лепестковый актиноморфный цветок не меняется при поворотах вокруг оси, проходящей через его центр, на угол, кратный 1/5 круга (таких поворотов можно сделать пять: на 72, 144, 216, 288 и 360 градусов) или при отражениях относительно 5 плоскостей симметрии. Такой цветок остается неизменным в 10 разных преобразованиях. Описанный комплекс преобразований актиноморфного цветка (точнее, его плоской двумерной схемы), удовлетворяет условиям группы: 5-лепестковый цветок описывается точечной группой с 10 элементами симметрии.

Авторы представляют компьютерную программу, созданную для расчета степени поворотной и зеркальной симметричности объекта. Цифровое изображение – в данном случае цветка – выражается числовой матрицей, то есть таблицей, содержащей информацию о яркости всех пикселей. Точность такой матрицы зависит от степени разрешения цифрового изображения и в принципе может быть сколь угодно высокой. Исходное изображение поворачивается на заданный угол. Матрица пикселей исходного изображения накладывается на матрицу повернутого, и яркости пикселей с совпадающими координатами перемножаются. Сумма значений таких произведений для всех пикселей области перекрывания матриц этих двух изображений, отнесенная к сумме квадратов яркостей пикселей исходного изображения, является количественным выражением симметричности при повороте на заданный угол.

Если после выполнения поворота оба изображения совпали полностью (например, при повороте идеального 5-лепесткового актиноморфного цветка на 1/5 круга), то степень симметричности равна 1. При неполном совпадении степень симметричности будет меньше единицы. Для антисимметричных объектов степень симметричности равна -1. Поворотную симметрию также можно изобразить графически в виде симметрограммы. Количество максимумов на симметрограмме говорит о порядке оси симметрии (в случае с 5-лепестковым актиноморфным цветком мы имеем дело с осью симмертии 5-го порядка).

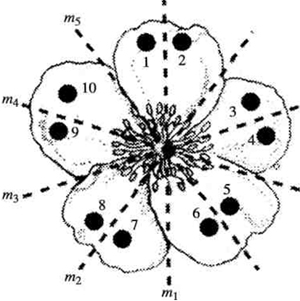
Подобная операция проделывается и при вычислении степени зеркальной симметричности.

Зигоморфные цветки, у которых в биологии принято учитывать только одну плоскость зеркальной симметрии, можно вращать точно так же, и находить неочевидную для глаз как поворотную, так и зеркальную периодичность.

Таким образом, применение предложенной программы, основанной на теории групп, позволяет предсказать потенциальные виды симметрии, т.е. найти все возможные элементы симметрии, существующие у данного организма, и оценить их количественно. Теория групп оптимизирует число операций, относительно которых необходимо рассчитывать степень симметричности. При сравнении природных псевдосимметричных объектов зачастую трудно или даже невозможно определить «на глазок», насколько цветок одного вида «правильнее» цветка другого вида. Именно здесь на помощь и приходит количественная оценка псевдосимметричности объектов, выявляющая локальные максимумы и скрытую периодичность. Максимумы как поворотной, так и зеркальной симметрии реальных цветков всегда меньше единицы в силу упомянутого «несовершенства» симметрии природных объектов. Симметричность цветка в целом удобно описывать всего одной числовой характеристикой – минимальным значением симметрии среди всех найденных локальных максимумов.

Авторы подчеркивают, что предложенный ими метод оценки симметричности является лишь одой из мер различия объектов, и должен использоваться совместно с другими принятыми в биологии методами.

Выявление групп симметрии и получение объективных статистических оценок биологических объектов может найти применение в эволюционных исследованиях перехода от актиноморфного к зигоморфному цветку при адаптации к опылению насекомыми. В работе приведены симметрограммы цветков ряда представителей сем. Бобовых (Fabaceae): от опыляемых ветром актиномофных цветков альбиции (Pithecellobium polycephalum) до зигоморфных цветков гороха (Pisum sativum), опыляемых насекомыми.

Предложенный математический аппарат также может стать эффективным инструментом биомониторинга, в котором отклонения от симметрии считаются показателем негативного воздействия факторов среды.