Повелитель окружностей
Задача
Рассмотрим обычный круг на плоскости. Если из него удалить одну точку — центр круга, — то оставшуюся фигуру можно будет разбить на непересекающиеся окружности: нужно просто взять семейство окружностей, центр которых совпадает с центром круга, а радиус меняется от нуля до радиуса круга. Слово «разбить» здесь означает, что каждая точка фигуры (круга без центра) обязательно попадет на какую-то окружность, а сами окружности не выходят за пределы круга.
А что будет, если удаленная из круга точка — не его центр, а какая-нибудь другая внутренняя точка, смещенная в сторону от центра? Можно ли такую фигуру разбить на непересекающиеся окружности? Выйдем в пространство: можно ли сферу без двух точек разбить на непересекающиеся окружности? А всё трехмерное пространство?
Подсказка
Во всех трех случаях ответ положительный — и круг без точки, и сферу без двух точек, и трехмерное пространство можно разбить на окружности.
При этом разбиения первых двух фигур — в некотором смысле одно и то же, потому что из одного можно получить второе при помощи стереографической проекции — это замечательное преобразование переводит (почти всегда) окружности в окружности. То есть достаточно придумать только одно из этих двух разбиений, а второе тогда получится «бесплатно».
Разбиение сферы без двух точек можно построить совсем «геометрически»: нужно вспомнить, что сечение сферы плоскостью — это окружность, и придумать, как правильно выбрать секущие плоскости. Разбиение круга без точки явно тоже несложно построить, но это чуть более «алгебраично».
Разбивать пространство на окружности можно по-разному. Один простой и изящный способ полагается на то, что пространство без одной точки можно представить в виде «луковицы» из концентрических сфер. И надо лишь придумать, как на каждой сфере выбирать по паре точек, чтобы эти точки тоже складывались в окружности.
Решение
Как уже говорилось в подсказке, ответы на все три вопроса задачи положительные. Начнем с разбиения на окружности круга без точки.
Пусть из круга удалена точка А. Для удобства будем считать, что радиус круга равен 1 и что эта точка расположена справа от центра круга О на горизонтальном радиусе (круг всегда можно повернуть, чтобы это было так) на расстоянии а от центра. Рассмотрим семейство окружностей с центрами на отрезке ОА, такое, что если центр отстоит от точки О на расстояние t (0 ≤ t < a), то радиус равен 1 − t/a. Например, у окружности с центром в середине отрезка ОА радиус равен 1/2.
Проверим, что такое семейство подходит. Во-первых, нужно убедиться, что окружности не пересекаются. Это так, потому что окружность меньшего радиуса всегда лежит внутри окружности большего радиуса. Докажем это. Пусть t1 < t2 — расстояния от центров двух окружностей до точки О (левее, то есть на расстоянии t1, лежит центр большей окружности, рис. 2). Тогда самая правая точка меньшей окружности (эта точка — самая далекая от центра большей окружности среди всех точек меньшей окружности) удалена от точки О на расстояние t2 + 1 − t2/a. От центра большей окружности она удалена на t2 + 1 − t2/a − t1. Вычтем эту величину из радиуса большей окружности, равного 1 − t1/a, чтобы убедиться, что радиус больше:
Это произведение положительно, потому что оба сомножителя больше нуля (первая скобка — в силу выбора радиусов окружностей, вторая — из-за того, что a < 1).

Рис. 2.
Формально, нужно еще проверить, что любая точка В круга (не совпадающая с А, естественно) попадет на какую-нибудь окружность из этого семейства. Можно, конечно, прямо найти центр этой окружности в зависимости от положения точки В, но больше подсчетов разводить не хочется, поэтому воспользуемся соображениями непрерывности: если мы начнем плавно двигать центр окружности от О к А, то расстояние от него до В будет меняться непрерывно (рис. 3).

Рис. 3. Слева — семь окружностей из нашего семейства, отмечены их центры. Справа — эти центры соединены отрезками с точкой B, видно, что расстояние до точки B меняется при смещении центра в сторону точки А
Нам даже не очень важно, как именно оно будет меняться: заведомо можно сказать, что оно будет или все время положительным, или однажды станет равным нулю, если точка В лежит на отрезке ОА, но главное, что оно сначала (когда центр еще рядом с точкой О) меньше 1, и в тот момент, когда центр приползет в точку А, это расстояние будет точно положительным, так как В не совпадает с А (рис. 4). Радиус окружности при таком движении меняется тоже непрерывно от 1 до 0. Поэтому в какой-то момент эти две величины сравняются, то есть точка В окажется на своей окружности из рассматриваемого семейства.
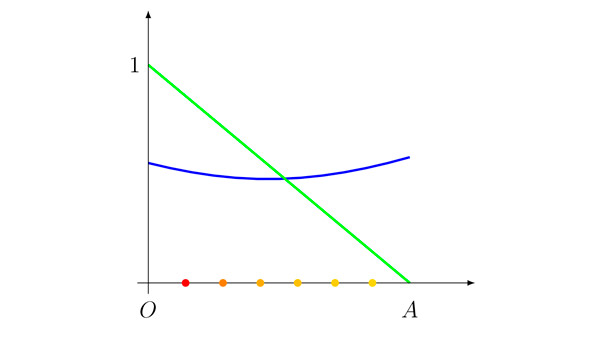
Рис. 4. На этом графике синяя линия показывает, как меняется расстояние до точки B по мере того, как центр окружности ползет по направлению к точке А. Цветными точками отмечено положение центров окружностей с рис. 3. Зеленая линия — изменение радиуса окружности в зависимости от положения ее центра на отрезке ОА. Пересечение синей и зеленой линий — а эти две линии обязательно пересекутся — это как раз и есть тот момент, когда точка B попадет на «свою» окружность
Теперь, как говорилось в подсказке, не составляет труда доказать, что и сферу без двух точек можно разбить на окружности. Для этого надо воспользоваться стереографической проекцией. Проведем какой-нибудь экватор на этой сфере, чтобы он разделил выколотые точки. Теперь поставим сферу на плоскость так, чтобы экватор был ей параллелен. При стереографической проекции из северного полюса сферы этот экватор перейдет в окружность на плоскости, а вся нижняя полусфера — в круг, ограниченный этой окружностью. Выколотая точка перейдет в какую-то точку внутри круга. Круг без этой точки можно разбить на окружности, а стереографическая проекция поможет «перенести» их обратно на сферу. Аналогично нужно поступить с верхней полусферой.
Разбиение сферы без двух точек можно построить и напрямую. Вот как это можно сделать. Построим в каждой из выколотых точек касательную плоскость к сфере. Эти плоскости либо пересекаются (по прямой), либо параллельны. Если они параллельны, то выколотые точки должны быть диаметрально противоположны друг другу. В таком случае окружности искомого разбиения получаются в сечении сферы плоскостями, которые перпендикулярны этому диаметру. Если же касательные плоскости все-таки пересеклись, то тогда нужно взять одну из них и начать поворачивать вокруг прямой пересечения в сторону второй плоскости. При таком вращении эта плоскость будет высекать на сфере нужные окружности.
Теперь переходим к самому интересному — разбиению всего трехмерного пространства на окружности. Для простоты введем координатную систему Oxyz. На плоскости Oxy построим окружности единичного радиуса с центрами во всех точках с координатами вида (4k + 1, 0). Как видно из рисунка 5, любая окружность с центром в начале координат пересекает это семейство окружностей в двух точках. Поэтому и любая сфера с центром в начале координат будет пересекать это семейство окружностей по двум точкам (почти всегда эти две точки лежат на одной окружности и только если радиус сферы делится на 4, то две точки — это точки касания сферы с двумя разными окружностями). Отсюда следует, что если удалить это семейство окружностей из пространства, то из каждой сферы пропадет по две точки (и еще начало координат, не попадающее ни на одну сферу, тоже пропадет). А значит, каждую из сфер без этих точек можно будет разбить на окружности.
Послесловие
Итак, мы разобрались с поставленными в задаче вопросами. Но сразу возникает много новых. Например, почему нужно было выкидывать точки из круга и сферы? Нельзя ли как-нибудь без этого? Оказывается, нельзя: ни круг, ни плоскость, ни сфера (и сфера без одной точки) не допускают разбиения на окружности. Рассуждение, которое это доказывает, строится от противного и вкратце выглядит так.
Допустим, что круг можно разбить на окружности. Тогда какая-то окружность ω1 точно проходит через его центр. Радиус этой окружности никак не больше половины радиуса исходного круга. Через центр ω1, в свою очередь, проходит какая-то другая окружность ω2, целиком лежащая внутри ω1 (потому что окружности не могут пересекаться), поэтому ее радиус не больше половины радиуса ω1. Через центр ω2 проходит еще какая-то окружность ω3... Тем самым получается последовательность вложенных друг в друга окружностей, радиусы которых стремятся к нулю. Есть ровно одна точка Х круга, которая лежит внутри каждой из этих окружностей (это следует из аналога леммы о вложенных отрезках для плоскости). Через эту точку должна проходить одна из окружностей разбиения (это не обязательно будет окружность из последовательности ωk), и у нее есть какой-то свой радиус. Тогда существует большой номер n, такой, что радиус окружности ωn уже достаточно маленький и она неминуемо пересечется с окружностью, проходящей через точку Х, а это невозможно, так как окружности разбиения не пересекаются. Противоречие, которое завершает доказательство.
Для плоскости и сферы работают аналогичные рассуждения.
Любопытно при этом, что плоскость можно покрыть окружностями в два слоя (то есть существует такое множество окружностей, что каждая точка плоскости принадлежит ровно двум окружностям из этого множества). Оставим это в качестве задачи для читателей. Узнать решение можно в «Задачном разделе» выпуска 9 сборника «Математическое просвещение». Кстати, там обсуждается и покрытие плоскости тремя слоями окружностей.
Там же описан и другой подход к решению задачи о разбиении пространства на окружности. Этот подход основывается на конструкции из вложенных друг в друга торов. Суть в следующем. Во-первых, внутренность тора — полноторие — можно разбить на окружности (осевая окружность тора плюс «нанизанные» на нее остальные окружности). Во-вторых, вложенными друг в друга полноториями можно итеративно заполнить все трехмерное пространство. Вот как это делается. Первый тор Т1 выберем произвольно (до конца абзаца слова «тор» и «полноторие» значат одно и то же). Возьмем окружность Ω1, которая проходит через центр тора перпендикулярно плоскости его осевой окружности и у которой центр лежит вне тора Т1, а радиус больше внешнего радиуса тора. Если прокрутить тор Т1 вокруг оси, которая проходит через центр Ω1 и перпендикулярна ей, то он заметет больший тор Т2 (правда, внутри Т2 останется полость, но ее легко «заполнить» окружностями). С тором Т2 можно проделать аналогичную операцию и получить еще больший тор Т3. Продолжая этот процесс, получим семейство торов, которое заполняет все пространство и тем самым получим разбиение пространства на окружности.

С разбиением торов на окружности связан еще один занятный сюжет, который довольно тесно связан и с серьезной математикой. Речь о так называемых окружностях Вилларсо. Это два семейства окружностей, которые «нестандартным» образом покрывают поверхность тора (см. рис. 6 и анимацию). Оказывается, что они позволяют построить разбиение трехмерной сферы (которая существует в четырехмерном пространстве) на равные окружности. Для сравнения, как мы только что видели, сфера (без проколов) вообще не допускает разбиения на окружности — не то что на равные! Подробно и с наглядными иллюстрациями этот непростой вопрос обсуждается в статье А. Акопяна «Окружности Вилларсо и расслоение Хопфа» («Квант» №5–6 за 2013 год).

Рис. 6. Два семейства окружностей Вилларсо на торе. Здесь они показаны красными и зелеными полосками, но воспринимать их нужно именно как окружности. Рисунок с сайта flickr.com
Можно также просуммировать длины всего семейства таких окружностей, площадь не будет равна площади исходного круга.
Последние задачи

















Рис. 1. Рассматриваемое семейство окружностей. Слева нарисованы 20 окружностей из этого семейства. Их центры равномерно распределены по отрезку OA. Справа нарисованы 50 окружностей из этого семейства. Вообще же в нем бесконечно много окружностей — каждой точке отрезка OA соответствует своя окружность, — поэтому нарисовать все семейство целиком невозможно