Сверхпроводимость
Глава 3. Природа сверхпроводимости
Квантовая механика
Так называется наука, которая заняла видное место в физике в 1920-х гг. Под квантовой механикой мы понимаем здесь нерелятивистскую квантовую теорию, изучающую законы движения микрочастиц при скоростях, гораздо меньших скорости света. Эти законы «работают» в основном на атомных масштабах расстояний, однако в некоторых случаях проявляются и в макромире. Можно назвать несколько квантовых явлений, которые наблюдаются почти без приборов, — сверхпроводимость, лазерный свет, магнитное упорядочение атомов ферромагнетика и др. Хотя эта наука уже полностью разработана, ее законы до сих пор непривычны для людей. Возможно, по этой причине их почти не изучают в школах. А может быть, наоборот: эти законы остаются непривычными, потому что их пока почти не изучают в школах.
Но рассказывая о сверхпроводимости, нужно обязательно вступать в царство квантовой механики. Без этого обойтись нельзя, так как само явление сверхпроводимости существенно квантовое, и его не удавалось понять, пока не было в основном завершено построение квантовой механики.
Для того чтобы придать механизму сверхпроводимости наглядность, будем рассматривать поведение электронов в кристаллах. Если бы это были частицы, подчиняющиеся обычной механике, то было бы удобно уподобить их бильярдным шарам.
Бильярдный шар находится где-то на бильярдном столе, он движется с какой-то скоростью. Мы привыкли, что его положение, скорость и энергия могут быть любыми, уж во всяком случае они никак не зависят от размеров бильярдного стола и высоты его бортов. Попробуем устроить на бильярде «твердое тело» — расставим шары правильными рядами. Это будет «кристаллическая решетка»,шары изображают тяжелые атомные остовы. Атомные остовы, или ионы, действительно намного тяжелее электрона. Напомним, что каждый протон и нейтрон, из которых составлено ядро атома, почти в 2000 раз тяжелее электронов.
Теперь пустим на бильярдный стол небольшой шарик, который будет сталкиваться с большими шарами. При этом энергия почти не будет теряться, если отношение их масс велико. Будем считать, что движение маленького шарика тормозится только за счет трения о сукно стола. И трение, и столкновения с большими шарами важны для понимания поведения электрона в кристалле. Конечно, в кристалле и то и другое свойство относятся к рассеянию электрона на ионах. При столкновении электрона с ионом изменяется направление его движения (как и при столкновении большого шара с очень маленьким). И те же столкновения обеспечивают «трение» — потерю энергии (трение о сукно).
Однако и после этого разъяснения «бильярдная» модель твердого тела вызывает недоумение. Решетка из больших бильярдных шаров отнюдь не кажется удобным «сосудом», «трубой» для движения шариков электронов. Попробуйте «включить ток» — толкнуть «электрон» сквозь «решетку». Если в «решетке» достаточно много шаров, протолкнуть электрон будет очень нелегко, сколько бы ни вмешиваться в его движение. Конечно, опытный игрок сможет пустить электрон точно между рядами шаров, но в металлическом кристалле ток течет отнюдь не только вдоль граней!
Таким образом, эта модель не годится для описания твердого тела.
Квантовый бильярд
Для устройства такого бильярда возьмем обычное плоское корыто, наполненное водой, волны на поверхности воды будут «электронами». Для нашей модели необходимо возбуждать волны с помощью длинной линейки, частицы изображаются плоскими бегущими волнами, а не круговыми волнами от упавшего в воду камешка.
К сожалению, весьма сложно создать в домашних условиях довольно большой полигон, чтобы спокойно наблюдать движение волны «электрона». После того как волна дойдет до стенки и отразится, возникнет рябь (интерференция), и надо будет ждать, пока вода успокоится для следующего опыта.
На квантовом бильярде можно попробовать устроить «кристаллическую решетку». Прикрепим к дну установленные правильными рядами палочки или что-нибудь еще в этом роде, так, чтобы они выступали над водой. Пустим на «кристаллическую решетку» плоскую волну «электрон». Она будет рассеиваться на каждой палочке — «атоме». От каждой палочки будут расходиться круги, которые затем, однако, сложатся, и мы увидим необычный результат: волна «электрон» пройдет через «кристалл». Конечно, на нашем кустарном бильярде она окажется искаженной, но можно доказать такое утверждение: если бы мы всё сделали совершенно точно, то и волна прошла бы без искажений.
Мы проиллюстрировали один из результатов квантовой механики: электрон проходит через правильную кристаллическую решетку, «не замечая» ее. Но это справедливо только для идеальной решетки. Любое отклонение от идеальности нарушает движение электронов и тем самым вносит вклад в электрическое сопротивление. Отклонения от идеальности возникают по двум причинам.
Первая причина — фононы. Атомы решетки всё время колеблются и отклоняются от средних положений — тем больше, чем выше температура. Именно отсюда возникает температурная зависимость электрического сопротивления, изображенная на рис. 3.
Вторая причина — дефекты. Это примеси — «чужие» атомы в узлах решетки; вакансии — отсутствие атома там, где он должен быть; «разрывы» решетки, которые называются дислокациями, и т. д. Видов дефектов набирается довольно много, они отвечают за остаточное электрическое сопротивление — ρ0 на рис. 3.
Шкала энергий
Вернемся к сверхпроводимости и прежде всего оценим, какую энергию выигрывает электрон при переходе от нормального состояния к сверхпроводящему. (Об этом выигрыше мы часто говорили ранее.) Ведь этот выигрыш — главное условие перехода. Физическая система не будет самопроизвольно менять свое состояние, если нет возможности уменьшить свою энергию.
«Сверхпроводящий выигрыш в энергии» легко определить, если еще раз обратить внимание на опыты в магнитном поле. Сверхпроводник вытесняет магнитное поле, и для этого — на создание токового экрана — тратится энергия. Расходуется на это как раз «сверхпроводящий выигрыш в энергии». Поэтому он равен энергии максимального магнитного поля, какое сверхпроводник еще способен из себя вытеснить. Напряженность такого поля Hc начали измерять вскоре после открытия сверхпроводимости и обнаружили, что выигрыш в энергии оказался удивительно маленьким.
Сверхпроводимость — весьма «хрупкое» явление. Но здесь придется приостановиться и извиниться, поскольку в физике нельзя сказать только «маленькая энергия», надо еще добавить, по отношению к чему она маленькая? Астрофизик с полным правом назовет энергию, излучаемую Солнцем, маленькой по сравнению с энергией, испускаемой при взрыве сверхновой звезды, но энергия Солнца заведомо больше всех наших земных энергий.
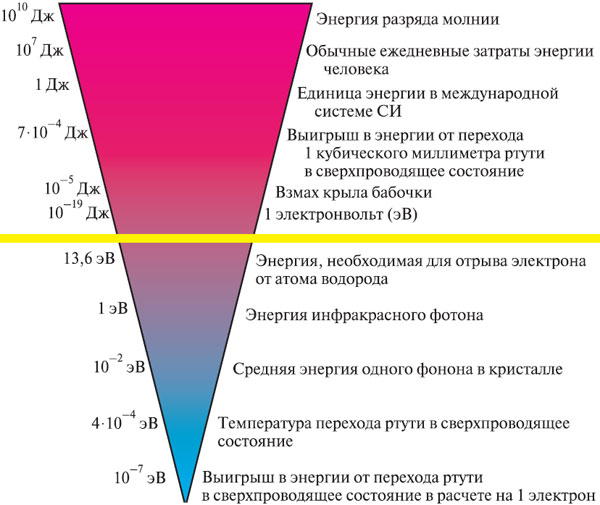
Возьмем за точку отсчета энергию 1 Дж (единица энергии в международной системе СИ, принятая в современной школе). Приблизительно это та энергия, которую затратит человек, чтобы подпрыгнуть на пару миллиметров. С человеческой точки зрения совсем немного — за день на передвижения, даже особенно не утруждаясь, человек тратит до десяти миллионов джоулей (рис. 29).
Нас, однако, интересует энергия куска вещества. Например, выигрыш в энергии для сверхпроводящей ртути составляет 7·10–14 Дж на каждый кубический сантиметр ее объема при абсолютном нуле температуры.
Эту энергию необходимо еще соотнести с количеством «действующих лиц» — электронов. В 1 см3 вещества приблизительно 1022–1023 атомов, у ртути приблизительно 4·1022 атомов в 1 см3. (Постоянная Авогадро составляет 6·1023 частиц на молярный объем. Атомный вес ртути 201 г, ее плотность 13,6 г/см3. Имея эти данные, легко вычислить молярный объем ртути и оценить концентрацию ее атомов.)Можно считать, что приблизительно таково же число электронов, составляющих электронную жидкость ртути; простые металлы отдают туда в среднем около одного электрона на атом. Выигрыш в энергии сверхпроводящей ртути составляет около 2·10–26 Дж в расчете на один электрон.
Это уже настолько маленькая величина, что удобнее перейти к другой единице энергии — электронвольту (эВ). Это энергия, которую набирает электрон, пролетающий ускоряющую разность потенциалов 1 В.
Обычно для того чтобы оторвать один электрон от изолированного атома или вырвать электрон из кристалла, требуется энергия несколько электронвольт. Такой же порядок имеет кинетическая энергия электрона в кристалле, и приблизительно такую же энергию несет квант видимого света, фотон — несколько электронвольт. Можно сказать, что это характерный атомный масштаб энергий. 1 эВ составляет примерно 1,6·10–19 Дж, гораздо больше, чем тот выигрыш в энергии, который мы оцениваем и который оказывается одной десятимиллионной долей электронвольта (10–7 эВ).
С чем еще можно сравнить эту величину? Энергии фононов, колебаний кристаллической решетки гораздо меньше, чем энергии электронов, — приблизительно в 1000 раз. Для электрона фонон — пушинка, которая может составить легкую помеху, но не более того. Средние энергии фононов порядка сотых долей электронвольта — это так называемые энергии тепловых излучений. (Если приложить к холодному кристаллу руку, то при передаче теплоты будут возбуждаться именно фононы.) Но ведь и энергия фононов, равная, скажем, 10–2 эВ, в 100 тысяч раз больше, чем «сверхпроводящий выигрыш в энергии» — 10–7 эВ. Более того, этот выигрыш даже меньше, чем температура перехода в сверхпроводящее состояние. Температура — мера кинетической энергии, и ее тоже можно измерять в электронвольтах. Температура перехода для ртути соответствует приблизительно 4·10–4 эВ. Эта величина еще в 4 тысячи раз больше, чем то изменение энергии электрона, которое происходит при переходе в сверхпроводящее состояние.
Сверхтекучесть
Пожалуй, первым среди коллективных движений квантовых частиц было понято явление сверхтекучести жидкого гелия при температуре ниже 2,17 К. Это имеет отношение и к истории сверхпроводимости, в связи с чем скажем несколько слов о сверхтекучести. Явление сверхтекучести «открывалось» в течение многих лет. Наибольший вклад в его изучение внес в 1938 году П. Л. Капица, а теорию явления построил в 1941 году Л. Д. Ландау.
Сверхтекучий жидкий гелий (который в этом состоянии называется гелием II в отличие от несверхтекучего гелия I) может протекать через тонкие капилляры, щели и вообще любые отверстия совершенно свободно, т.е. совсем без трения. (Речь идет о сверхтекучести наиболее распространенного изотопа гелия 4Не, а есть еще сверхтекучесть изотопа гелия 3Не. Свойства этих явлений сильно различаются.) Это весьма похоже на сверхпроводимость электронной жидкости, только заряд атомов гелия равен нулю, поэтому тока при сверхтекучести не возникает. Однако некоторые другие свойства гелия II и электронной жидкости сверхпроводника очень похожи. Можно сказать, что сверхпроводимость — это сверхтекучесть заряженной жидкости, а сверхтекучесть — это «сверхпроводимость» нейтральной жидкости. Сверхпроводимость и сверхтекучесть — весьма близкие по своей природе явления. Оказывается, и гелий II ведет себя как смесь двух жидкостей — сверхтекучей и нормальной.
Сверхтекучая часть гелия II движется совсем без трения и одновременно совсем не переносит теплоты; в нормальной части содержится вся теплота, имеющаяся в жидкости; и эта часть жидкости испытывает трение.
Сосуществование сверхтекучей и нормальной жидкостей ярче всего демонстрирует опыт, схема которого изображена на рис. 30.
Как же понять это движение без трения? Представьте, что все частицы жидкости как бы сцеплены вместе и ни одну нельзя отделить, не разрушив всё состояние. Речь идет о квантовых состояниях и о квантовых законах, поэтому аналогия в повседневной жизни вряд ли найдется. Но можно вспомнить одну из самых первых задач квантовой механики, которую решил датский физик Нильс Бор в 1912 году. Это задача о строении атома.
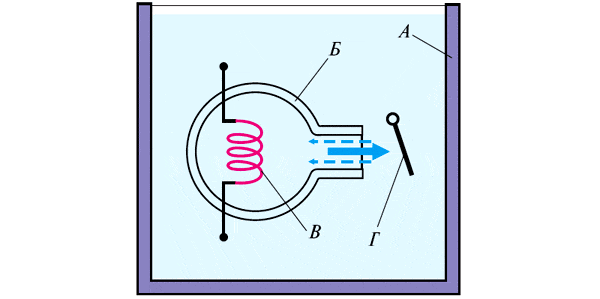
Рис. 30. В большой сосуд А с гелием II помещена колбочка Б. В широкой части колбочки встроена нагревательная спираль В — если включить извне ток, то можно нагревать жидкий гелий только внутри колбочки. Узкая часть колбочки открыта, жидкий гелий может втекать или вытекать из нее свободно, но перед отверстием расположено легкое крылышко Г, отклонение которого при малейшем движении жидкости можно наблюдать. Если начать нагревать спираль, крылышко сразу показывает, что из колбочки начинает вытекать гелий. Вместе с тем количество жидкости в колбочке не уменьшается сколь угодно долго, а значит, гелий должен не только вытекать, но и втекать. Многочисленные опыты показывают, что в узкой части колбочки в каждой точке сосуществуют два противоположных течения — нормальное, уносящее из колбочки теплоту, и сверхтекучее, доставляющее туда жидкость, причем сверхтекучее течение не оказывает давления на крылышко
Атом и квантовые состояния
К 1912 году было твердо установлено, что атом состоит из тяжелого положительно заряженного ядра и легких отрицательно заряженных электронов. Но было не понятно, как они могут сочетаться в атоме. В соответствии с законами классической физики вращающийся вокруг атома электрон движется ускоренно. Ускоренно движущийся заряд должен излучать электромагнитные волны и тем самым терять энергию, а значит, довольно быстро упасть на ядро.
Решение Бора таково: вращающиеся вокруг ядра электроны находятся в определенных квантовых состояниях. Они поглощают или излучают энергию только при переходе из одного квантового состояния в другое, лежащее выше или ниже по энергии. По аналогии со сверхпроводимостью и сверхтекучестью можно сказать, что электрон в своем состоянии «движется по орбите без трения». Ничто не может помешать ему, если энергия «помехи» меньше, чем энергетическое расстояние между состояниями.
Теперь попробуем перенести те же выводы на жидкость в целом. Пусть у нее есть наинизшее по энергии состояние, которое называется основным, и следующие, вышележащие. Если разница в энергии между этими последующими состояниями и основным сколь угодно мала, то жидкость находится в нормальной фазе, она легко принимает и отдает энергию, а ее движение происходит с трением.
Если же вышележащие состояния отделены от основного некоторым интервалом, который называется щелью (энергетической), становится возможным движение без трения. Щель мешает жидкости переходить в другое состояние. Но, конечно, если воздействие (например, магнитное поле, сверхпроводящий ток, нагрев) достаточно большое — больше критического, тогда щель разрушается.
Таким образом, сверхпроводимость и сверхтекучесть — прямое проявление квантовых свойств огромных коллективов частиц.
Квантовые жидкости
Мы привели два примера квантовых жидкостей: жидкий гелий, где при низких температурах возникает сверхтекучесть, и электронную жидкость, где при низких температурах возможна сверхпроводимость, которая есть не что иное, как сверхтекучесть жидкости заряженных частиц. Но если для жидкого гелия наши качественные объяснения почти достаточны, то далеко не так просто обстоит дело со сверхпроводимостью.
Названные жидкости — представители двух классов квантовых жидкостей, которые могут существовать в природе. Дело в том, что на два класса делятся все частицы в зависимости от значения присущего им спина. Спин — одна из квантовых характеристик любой частицы. К сожалению, аналогии для нее в окружающей нас жизни нет. Очень условно можно говорить о спине электрона как о характеристике его вращения вокруг своей оси, т.е. представлять электрон чем-то вроде волчка. Однако в то же время стоит твердо помнить, что никакого вращения на самом деле нет. А есть спин.
Спин может принимать целые или полуцелые значения. (Единицей измерения спина является квантовая постоянная Планка ħ ≈ 1,05·10–27 эрг·с1.) Если частица имеет целый спин: 0, 1, 2, и т.д., она называется бозе-частицей, в честь индийского физика Ш. Бозе. Если частица имеет полуцелый спин: 1/2, 3/2, 5/2 и т.д., она называется ферми-частицей, в честь итальянского физика Э. Ферми. Свойства двух видов частиц значительно различаются.
Спин атомов гелия равен нулю, поэтому жидкий гелий представляет собой пример бозе-жидкости. Кардинальное свойство бозе-частиц — стремление занимать одно состояние, т.е. стремление всех частиц жидкости как бы притягиваться друг к другу. Речь идет, конечно, не о реальном притяжении, а о самом простом представлении о свойствах бозе-частиц. Очень удачным нам кажется эпиграф, который предпослал рассказу о них известный английский физик Дж. Займан: «Чем нас больше соберется, тем нам будет веселей».
Для бозе-жидкости естественно выполнение условий, необходимых для движения без трения.
А для ферми-жидкости дело обстоит наоборот: никакие две ферми-частицы не могут обладать одинаковым набором характеристик. Это абсолютный закон, который называется принципом Паули, в честь известного швейцарского физика В. Паули. Этот закон задает как бы отталкивание одинаковых ферми-частиц друг от друга, а электроны обладают спином 1/2, и электронная жидкость является ферми-жидкостью.
Плотность (концентрация) электронов в простых металлах очень велика (1022–1023 электронов в 1 см3). Очень велико и число состояний, которые эти электроны занимают, — каждому свое в отличие от бозе-жидкости. Поэтому и спектр энергий электронов в простых металлах очень широк, а их средняя кинетическая энергия достигает нескольких электронвольт.
Очень долго было совершенно непонятно, как в этих условиях устроить щель между состояниями электронной жидкости, да и как может устойчиво существовать столь маленькая щель (она по порядку величины соответствует критической температуре) на фоне столь больших энергий электронов. Единственный принципиально возможный путь — создать из электронов бозе-частицы. На словах это просто: достаточно связать электроны в пары. Тогда суммарный спин пары либо 0, либо 1, и в любом случае пара в целом является бозе-частицей.
Коль скоро электроны образовали пары, физику становится понятным, почему возникает сверхпроводимость. Но вот с какой стати образовывать пару двум отрицательно заряженным частицам, которые сильно отталкиваются по закону Кулона. Можно оценить, что эти силы отталкивания сообщают двум «соседним»2 электронам ускорение разлета порядка 1020 ускорений свободного падения (которое равно, как известно, g ≈ 9,8 м/с2). Конечно, в электронной жидкости взаимные отталкивания уравновешиваются и реально таких ускорений электрон не испытывает. Но как жить в паре с подобным соседом?
Электрон-фононное взаимодействие
В главе «Физика сверхпроводимости» мы представили еще одно действующее лицо этой книжки — фононы. Именно они помогают объединить электроны в пары.
Напомним, что фононы — это волны кристаллической решетки металла. Однако равным образом можно представлять их как частицы, что принято в квантовой механике. Далее, мы писали, что идеальной кристаллической решетки электрон «не замечает», поэтому о рассеянии электрона на колеблющейся кристаллической решетке можно говорить как о рассеянии на фононах.
При рассеянии электрона на волне решетки или, иными словами, столкновении электрона с фононом меняются энергии, скорости и направления движения этих частиц, но соблюдаются законы сохранения энергии и импульса. Можно мысленно представить картину столкновения двух бильярдных шаров, однако электрон и фонон слишком разные по своей природе частицы, поэтому точнее другой образ: электрон поглощает фонон, принимая его энергию и импульс, или электрон испускает фонон, запускает колебание решетки, отдавая ей часть своей энергии. Все подобные процессы вкупе называются взаимодействием электронов с фононами.
В нормальном состоянии это взаимодействие порождает электрическое сопротивление: электрон в своем движении возбуждает колебание решетки, а сам при этом слегка тормозится. Оказывается, взаимодействие электронов с фононами обеспечивает не только сопротивление, но и его исчезновение при низких температурах. Оно способствует столь желанному объединению электронов в пары.
Связывание электронов в пары
Чтобы понять, как это происходит, проследим дальнейшую судьбу фонона, который был возбужден электроном. Итак, в решетке пролетел электрон и вызвал колебание ионов, расположенных в узлах решетки. Электрон несет отрицательный заряд, а ионы заряжены положительно. Поэтому ионы слегка притянутся к пролетевшему электрону (рис. 31). Но ионы гораздо тяжелее электрона, следовательно, их движение более медленное. Электрон уже «давно» пролетел, а ионы еще только подтянулись к тому месту, где он был. Значит, в этом месте образовался (на некоторое время) небольшой избыточный положительный заряд, и уже другой летящий мимо этого места электрон почувствует его и изменит траекторию своего движения, притянется к этому месту.
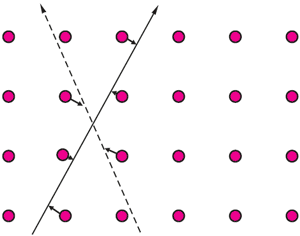
Рис. 31. Кружки изображают упорядоченные в решетку атомные остовы, ионы. Сплошная и штриховая линии показывают как бы траектории движения двух притягивающихся через посредство фононов электронов
Таким способом фононы создают слабое притяжение между электронами. Но притягиваются электроны, находящиеся на больших расстояниях. Ведь для того чтобы второй электрон (см. рис. 31) притянулся ионами, первый должен уже далеко улететь, иначе его отрицательный заряд «перебьет» всё притяжение. Электроны, находящиеся вблизи, отталкиваются, как и положено двум отрицательным зарядам по закону Кулона, а на достаточно больших расстояниях они притягиваются за счет фононов. На больших расстояниях отталкивание двух электронов не мешает, так как вокруг и между обоими электронами много положительных ионов и других электронов, и все силы притяжения и отталкивания уравновешиваются.
Притяжение между электронами приводит к связыванию их в пары, которые называются куперовскими, в честь американского ученого Л. Купера. Первое сравнение, которое приходит в голову, — возникла «электронная» молекула. Но это не совсем так. Атомы в молекулах находятся рядышком, а для того чтобы пропустить «сквозь» молекулу какой-то «чужой» атом, нужно затратить большую энергию, и при этом молекула разрушится. В куперовской паре электроны находятся на большом расстоянии, которое может быть в тысячи раз больше, чем среднее расстояние между электронами, т.е. между двумя составляющими пару электронами свободно «бегает» огромное количество других электронов, относящихся к другим парам. Это как бы большущая толпа, в которой вы видите своего друга далеко от себя, но всё же не теряете его из виду.
Среднее расстояние между электронами в паре обозначается греческой буквой ξ и называется длиной корреляции. Это расстояние, на котором электроны чувствуют друг друга и на котором существенно изменяются сверхпроводящие свойства. Значения для разных сверхпроводящих материалов различны. В таблице дано несколько примеров.
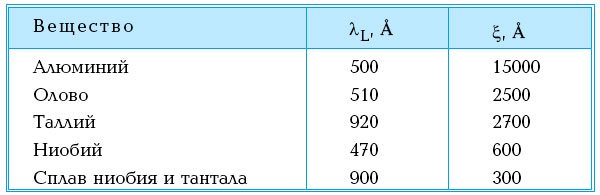
Значения длин ξ и λL (лондоновская глубина проникновения магнитного поля) указаны для температуры, стремящейся к абсолютному нулю.
Граница сверхпроводника
Две длины характеризуют каждый сверхпроводящий материал — длина корреляции ξ и глубина проникновения магнитного поля λL.
Магнитное поле в сверхпроводнике сильно изменяется на длине λL, а на длине ξ сильно изменяется количество сверхпроводящих электронов, т.е. электронов, связанных в куперовские пары. Особенно наглядно это видно на границе сверхпроводника. На рис. 32 схематически показаны: справа (зеленым цветом) сверхпроводник, в глубине которого количество ns сверхпроводящих электронов постоянно, а к границе с нормальной фазой начинает спадать; слева существует постоянное магнитное поле, которое в сверхпроводнике экранируется и от его границы вглубь спадает.
Видно, что возможны две ситуации. Первая: длина ξ больше глубины λL (см. рис. 32, а). Иметь такую границу невыгодно энергетически, тут образуется целая область, где магнитное поле уже вытеснено (на что требуется энергия), а сверхпроводящих электронов мало и сверхпроводящего выигрыша в энергии еще нет. Так выглядит граница сверхпроводника I рода. На образование такой границы нужно затрачивать энергию, поэтому в промежуточном состоянии таких границ возникает не очень много. Да и вообще сверхпроводимость I рода легче разрушить.
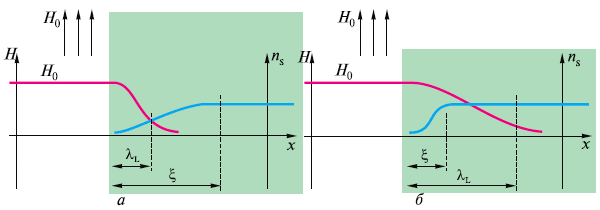
Рис. 32. Граница сверхпроводящей (зеленый цвет) и нормальной (белый цвет) фаз. Зависимость напряженности магнитного поля и количества сверхпроводящих электронов от расстояния поперек границы: а — сверхпроводник I рода; б — сверхпроводник II рода
Совсем другое дело — сверхпроводник II рода (см. рис. 32, б). Здесь длина λL больше ξ (если точно, то к сверхпроводникам II рода относятся материалы, для которых λL > ξ√2). Получается, что магнитное поле спадает плавно, вытесняется медленнее, чем электроны связываются в пары, и возникает сверхпроводящий выигрыш в энергии. Эта ситуация энергетически выгодна, и в сверхпроводнике II рода таких границ появляется много — в виде вихрей. Вихрь ведь и есть такая граница, только свернутая в трубку, в середине которой магнитное поле.
Два главных свойства сверхпроводника
Таковыми являются отсутствие электрического сопротивления и наличие эффекта Мейснера. Теперь посмотрим, как они связаны с описанным механизмом сверхпроводимости.
Действительно, куперовские пары электронов могут двигаться без трения (рис. 33). Дело в том, что электроны в такой паре разделены большим расстоянием, а энергии их одинаковы. Пусть один электрон наталкивается на дефект, но не может рассеяться произвольно, ведь его «держит» второй, спаренный электрон. В такой ситуации оба связанных электрона лишь изменяют направление своего движения, однако не меняют своей энергии, а это и значит, что они движутся без трения.
Электроны, по тем или иным причинам не связанные в пары, ведут себя обычно, их мы называли нормальными. В сверхпроводящем состоянии некоторое количество пар разрушается под влиянием температуры, магнитного поля и т.п.

Рис. 33. Условное изображение рассеяния куперовской пары электронов на дефекте. Кристаллическая решетка обозначена маленькими кружочками, а дефектный узел — большим черным кружком посередине. Два движущихся в противоположных направлениях электрона куперовской пары показаны штриховыми линиями. Расстояние между ними гораздо больше, чем расстояние между соседними узлами кристаллической решетки
В куперовскую пару связываются электроны с противоположно направленными спинами. Это стремление противоречит стремлению магнитного поля выстраивать спины вдоль своего направления. Две эти противоположности совместить никак нельзя. Сильное магнитное поле «распаривает» электроны и уничтожает сверхпроводимость. Слабое же магнитное поле само вытесняется сверхпроводящими электронами. Они подстраиваются и изменяют свое движение так, чтобы экранировать поле.
И наконец, скажем заключительные в этой главе слова: сколь бы сложным ни казалось явление сверхпроводимости после нашего описания, на самом деле оно еще сложнее. Сверхпроводимость обусловлена коллективным, а не только парным поведением электронов. Взаимосвязаны движения не только двух электронов в куперовской паре, но и всех пар между собой. Для тех, кто увлекается электро- или радиотехникой, такое свойство будет особенно понятным: можно сказать, что все пары движутся в фазе. И эта фаза — вполне реальная квантовая характеристика сверхпроводника, существование которой доказано на опыте.
1 Изначально введенная Планком постоянная h = 2 πħ.
2 «Соседним» — значит, находящимся на среднем друг от друга расстоянии.











Рис. 29. Шкала энергий