Что перевесит?
Обычно мы предлагаем задачи по физике, которые так или иначе касаются современной науки. В этот раз, поддавшись предновогоднему настроению, мы предлагаем отойти от этой традиции и подумать над четырьмя задачками попроще. Сразу скажем, что одна из них недавно широко обсуждалась в интернете, хотя, конечно, это обсуждение не сопровождалось такими бурными спорами, какие несколько лет назад вызвала задача «Взлетит или не взлетит?».
Задача
Итак, все четыре задачи — на тему «какая чашка весов перевесит»; их условия проиллюстрированы на рис. 1. В каждой задаче на обеих чашках весов находятся одинаковые контейнеры и, за исключением третьей задачи, с одинаковыми предметами внутри. В задачах 3 и 4 количество воды в контейнерах одинаковое, а внешние подвесы считаются прочно закрепленными на столе.
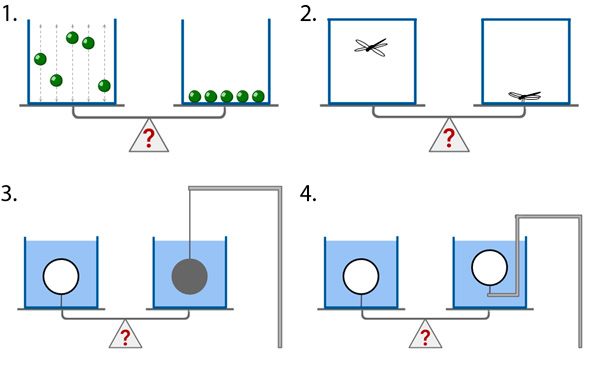
1. В первой задаче в обоих контейнерах находится одинаковое количество металлических шариков. В левом контейнере они постоянно подпрыгивают на некоторую высоту, абсолютно упруго отскакивая от дна. В правом — неподвижно лежат на дне. Для простоты можно считать, что шарики подпрыгивают вертикально вверх и не сталкиваются друг с другом. Кроме того, их очень много и прыгают они хаотично, так что дрожанием показаний весов можно пренебречь.
2. Во второй задаче в двух герметично закрытых контейнерах есть по стрекозе. В левом контейнере стрекоза зависла в воздухе на определенном месте, в правом — она спокойно сидит на дне. Можно считать, что зависшая стрекоза уже висит там достаточно долго, а не только что взлетела.
3. В третьей задаче добавляется вода. В обоих контейнерах налито одинаковое количество воды и в нее погружены два шарика одинакового радиуса. В левом контейнере легкий шарик от настольного тенниса привязан за ниточку ко дну. В правом — тяжелый металлический шарик подвешен на нити к подвесу, который закреплен отдельно от весов с контейнерами. Оба шарика полностью погружены в воду.
4. В четвертой задаче левая чашка весов ровно такая же, как в третьей, а в правой на изогнутом твердом, но очень тонком креплении удерживается второй точно такой же шарик от настольного тенниса.
В каждой из этих четырех задач выясните, какая чашка весов перевесит: левая, правая или же весы будут в равновесии.
Подсказка
Подсказка в этих задачах — это уже почти ответ. Поэтому дадим только три осторожных намека:
(1) при усреднении по времени весы чувствуют весь объект на чашке целиком, а не отдельные его части,
(2) помни об Архимеде!
(3) помни о Ньютоне!
Решение
1. В первой задаче обратим внимание на положение центра масс всей системы прыгающих шариков. Раз шарики отскакивают абсолютно упруго, то они всегда подпрыгивают на одну высоту. Прыжки вверх-вниз всех шариков происходят не синхронно, а хаотично, поэтому их общий центр масс практически не прыгает, а держится на некоторой высоте. Сама эта высота не важна (впрочем, упомянем, что она составляет 2/3 от максимальной высоты); главное, что центр масс неподвижен. Поэтому если рассмотреть всю совокупность шариков как общую единую систему, лежащую внутри контейнера, то эта система лежит там неподвижно — несмотря на то, что внутри нее происходит некоторое движение. На эту систему действует сила тяжести и сила реакции со стороны дна контейнера; раз центр масс покоится, значит эти силы равны по модулю. Получается, что контейнер с прыгающими шариками в среднем весит столько же, столько контейнер с неподвижными шариками. Весы будут в равновесии.
2. Во второй задаче снова используем тот же подход. Хоть висящая в воздухе стрекоза не касается непосредственно стенок, она держится за счет отталкивания воздуха вниз своими крыльями. Центр масс стрекозы неподвижен, поэтому эта сила отталкивания компенсирует действующую на нее силу тяжести.
Но раз воздух поддерживает стрекозу с некоторой силой, то значит и стрекоза давит на весь воздух в целом с той же силой, но только направленной вниз. Это третий закон Ньютона — сила действия равна силе противодействия, но только они направлены в противоположные стороны. Просто обычно этот закон применяют к твердым телам, но он годится и для «опоры о воздух». А раз центр масс воздуха в закрытом контейнере тоже неподвижен, то эта сила передается дальше на дно контейнера. Такие образом, наличие зависшей в воздухе стрекозы приводит к дополнительной силе давления на весы, равной весу самой стрекозы. Поэтому и здесь весы будут показывать равновесие.
Еще раз подчеркнем: для задачи взвешивания «внутренняя жизнь» составной системы не важна, как бы богата она ни была. Главное — это какие силы на нее действуют в целом и как движется центр масс этой системы. Если центр масс неподвижен, а снаружи никто на систему не давит, то сила давления на чашку весов будет равна силе тяжести. Условия задачи гарантируют, что центр масс системы «контейнер + воздух + стрекоза» неподвижен, поэтому для взвешивания важна только масса этой системы. А уж как там стрекоза держится в воздухе — дело десятое.
3. Переходим к третьей задаче, которая, собственно, и обсуждалась в интернете. На левой чашке весов контейнер с водой и привязанным шариком. Эти подробности отражают лишь внутреннее устройство этой системы, задачи взвешивания они не касаются. Эта система неподвижна, никаких внешних сил, помимо гравитации и сил реакции опоры, на нее не действует, поэтому она давит на весы просто со своей силой тяжести. Так что легкий шарик здесь присутствует только для отвлечения.
В правой части есть особенность — дополнительные (по сравнению с левой чашкой) внешние силы. Это, прежде всего, дополнительная сила тяжести, действующая на тяжелый шарик, а также некая сила подвеса. Эти две дополнительные силы тянут всю систему «контейнер + вода + тяжелый шарик» в разные стороны: сила тяжести вниз, сила подвеса вверх. Но компенсируют ли они друг друга?

Рис. 2. Силы, обеспечивающие равновесие тяжелого шарика в задаче 3. Силы, показанные красным, являются внешними для всей системы «контейнер + вода + тяжелый шарик»; именно они важны для расчета показаний весов
Это можно выяснить из условий равновесия, записанных отдельно для шарика (ведь он тоже покоится!), см. рис. 2. Вниз его тянет сила тяжести mg, вверх — сила Архимеда FA, а также сила подвеса на нити Fподвес, которая отсюда получается равной mg − FA. Внешний подвес хоть и тянет вверх контейнер с водой и шариком, но не полностью компенсирует силу тяжести шарика. Поэтому совокупный эффект от двух дополнительных внешних сил, действующих на правую чашку, есть сила, давящая вниз и равная mg − Fподвес = FA.
Итак, не только вода выталкивает шарик с силой Архимеда, но — по третьему закону Ньютона — и шарик опирается на воду, а значит, он давит на весы вниз с той же силой. В этой задаче правая чашка весов перевесит.
Еще раз подчеркнем: тяжелый шарик не висит на нити просто так, в отрыве от контейнера с водой. За счет силы Архимеда он механически сцеплен с контейнером — ровно так же, как стрекоза была механически сцеплена с закрытым контейнером. Поэтому их можно рассматривать как единую систему, в которой силы передаются от одной части к другой, а значит, часть силы тяжести шарика передается и на весы.
4. Четвертая задача представляет собой лишь вариацию третьей. Здесь выталкивающая сила Архимеда такая же, но сила тяжести намного меньше (шарик легче воды), поэтому сила реакции со стороны опоры тоже тянет шарик вниз. Получается, обе внешние силы действуют на систему «контейнер + вода + шарик» вниз и их сумма равна той же силе Архимеда. Они сообща давят на весы, поэтому и здесь правая чашка весов перевесит.
Послесловие
Из этих задач можно вынести несколько простых, но полезных уроков на будущее.
Во-первых, детальный разбор системы на отдельно движущиеся кусочки не всегда полезен. Например, в самой первой задаче можно легко сосчитать скорость каждого шарика перед ударом о дно, изменение его импульса в процессе удара и время между последовательными ударами. Тогда, поделив изменение импульса на время полета, можно найти среднюю силу от одного шарика и убедиться, что она равна mg. Но уже в чуть более продвинутой задаче это вычисление быстро усложняется. Например, вы можете считать, что удар шариков не абсолютно упругий и что скорость отскока составляет 0,999 от скорости перед ударом. Как тогда изменятся показания весов? Вычисления в лоб станут намного более громоздкими и неудобными. Зато метод слежения за центром масс, описанный тут, по-прежнему будет простым и быстро даст ответ.
Еще сложнее дело обстоит во второй задаче. В принципе, можно попытаться явно описать, хотя бы в рамках какого-то предположения, движение потоков воздуха под крыльями и вблизи стенок (причем всех стенок, а не только пола). Но этот безумно сложный расчет тут просто и не нужен: если все процессы воздушных течений в среднем стационарны, то суммарная сила давления на дно легко находится из законов механики.
Во-вторых, не надо забывать, что механические законы применимы не только к твердым телам, но и к жидкости и газу. Они, конечно, подвижны, они не держат форму под искривляющим давлением. Но, по крайней мере, они обеспечивают механический контакт между погруженным телом и стенками сосуда. И, когда надо, через этот механический контакт может передаваться механическое усилие.
Кроме того, к жидкостям и газам можно тоже применять законы Ньютона — как бы непривычно это ни казалось на первый взгляд. Вода выталкивает тело с силой Архимеда. И это значит, по третьему закону Ньютона, что и тело давит на воду с той же силой. Ну а если тело активно барахтается в толще воды и пытается тем самым предотвратить дальнейшее погружение, то оно давит на воду уже всей своей силой тяжести.
В-третьих, снова напомним важное правило механики: если мы интересуемся системой в целом, то неважно, какие там действуют внутренние силы (вспомним про барона Мюнхаузена, который тянул себя за волосы из болота). Главное, это как движется общий центр масс и какие внешние силы действуют на систему. Однако, как показывают задачи 3 и 4, иногда для расчета внешних сил может потребоваться заглянуть и внутрь системы.
Ну и наконец, надо добавить, что задача 3 — это чуть усложненная версия знаменитого метода Архимеда по определению средней плотности тела, метода, от которого, по легенде, и пошло восклицание «Эврика!». Представьте себе, что в роли подвеса в задаче 3 выступаем мы сами. Мы удерживаем шарик на ниточке, прикрепленной к ручным весам, причем эти ручные весы показывают силу Fподвес. Тогда, произведя измерения в воздухе и в воде, мы вычтем одно из другого и получим выталкивающую силу Архимеда. Отсюда мы находим объем тела, а затем и его среднюю плотность.
-
Немного непонятен в первой задаче логический переход: "раз центр масс покоится, значит, эти силы равны по модулю". А почему он, собственно, покоится? Может быть, он двигается вниз с ускорением (чашка перевешивает) и эти силы не равны? То, что центр масс системы шариков в принципе может покоиться при соответствующей силе реакции опоры, не означает, что он покоится при силе реакции, равной mg (а она задана точно второй чашкой).
Мне бы больше было понятно объяснение, что, допустим, сначала шарики покоились на обеих чашках, причем в левой они лежали на невесомых столбиках разной высоты. Потом столбики резко выбили и шарики начали падать и отскакивать.-
Смотрите, каждый шарик отскакивает на ту же высоту, значит если усреднить его положение центра масс по периоду подскока, т.е. найти его усредненный центр, то он будет неизменен и через период, и через два, и вообще всегда. Поэтому общий центр тяжести не может постоянно двигаться вверх или вниз, через период он точно должен вернуться на место (для простоты считаем пока, что периоды всех шариков одинаковы). Максимум он может периодические двигаться вверх или вниз. Так могло бы быть, если бы шарики прыгали синхронно — т.е. подавляющее большинство идет вниз, а потом идет вверх. Но в задаче сказано, что они движутся хаотично, так что все эти колебания центров масс компенсируются в общем ц.м. Конечно, останется мелкая дрожь из-за неабсолютно точной компенсации, но ею по условиям предлагеется пренебречь. Еще лучше для разных периодов — даже если бы там была какая-то начальная синхронность, она исчезнет спустя несколько подскоков.
То, что предлагаете вы, это не выход. Вы как бы стесняетесь усреднять по периоду. Вы обратили внимание только на начальный момент времени, а не на все движение.-
У вас в качестве исходной посылки для решения задачи выступает утверждение, что центр масс покоится. Естественно, из этого можно получить только тот вывод, что весы находятся в равновесии.
Но само это утверждение не следует напрямую из условия задачи (по крайней мере, на школьном уровне). Если предположить, что левая чашка перевешивает (допустим, из-за наличия в системе дополнительной энергии или импульса), то центр масс движется вниз с ускорением, сила тяжести больше силы реакции опоры, и каждый шарик в верхней точке подъема опускается все ниже с каждым прыжком.
Я предложил аналогию, которая показывает эквивалентность системы двигающихся шариков с покоящимися на столбиках, так как очевидно, что после выбивания столбиков дополнительной массы, энергии и импульса в систему не вносится, а значит, и положение чашек не изменится. Можно наоборот, рассмотреть ситуацию, когда под каждый прыгающий шарик в верхней точке траектории мы подставляем столбик (опять же не меняя массу, энергию и импульс системы). Очевидно, что получившаяся конструкция весит столько же, что и просто шарики на правой чашке.
-
-
-
Энергия, расходуемая стрекозой на полет на месте, целиком и полностью переходит в тепло, нагревающее окружающую стрекозу воздух вместе с самой стрекозой.
А в первой задаче - да, строго говоря, при учете эффектов СТО вес левой чашки увеличится, а при учете зависимости силы тяжести от высоты - уменьшится. :)-
<при учете зависимости силы тяжести от высоты - уменьшится.
Поясните, пожалуйста, ведь шарики ударяются о левую чашку на той же высоте, на которой лежат в правой чашке.-
Ударяются но той же, но летают выше. Соответственно, вертикальный импульс за то же время накапливают меньше.
-
Или же, — возвращаясь к методу с усреднением, — центр тяжести системы прыгающих шариков лежит выше, поэтому на него действует меньшая сила тяжести.
-
В задачах 1 и 2 центр масс левой чашки выше, поэтому гравитационное взаимодействие слабее и левые чашки легче.
-
-
Для того чтобы избавиться от этого различия центра тяжести от центра масс давайте видоизменим условия задачи 2. Внутри замкнутого объема не стрекоза, а муха. Слева муха сидит на дне, справа на потолке. Муха имеет массу, а банка не имеет массы (масса банки на много меньше массы мухи, банка из твердого дыма:). Правая чаша легче, потому что муха выше.
-
-
-
-
-
-
Ну, вы уже взялись рассуждать, т.к. высказали мнение, что она «сильно абстрактная с точки зрения законов сохранения энергии.» Напротив, она совершенно конкретная — все величины считаются в лоб.
> По-идее чаша с прыгающими шарами должна перевесить, т.к. она заключает большее количество энергии,
А скажите, что взвешивают весы? Что физически они измеряют? Энергию? Нет, они измеряют силу давления на чашку весов. В том-то и дело, что им наплевать на энергию.
Аналогично про стрекозу. Да, она тратит энергию, и тем самым она нагревает воздух и увеличивает общее давление в сосуде. Ну и что? Весы же не взвешивают температуру или изостатическое давление? Весы взвешивают силу давления на чашку.
-
Так, возможно, короче с точки зрения формулировки, но с педагогической точки зрения это опасно. Вы сейчас не только разбили систему на части (иногда люди запутываются именно за счет излишнего разбиения на части), но и убрали из рассмотрения одну часть (сам шарик). Представьте теперь, что кто-нибудь попробует использовать буквально это рассуждение к еще более простой задаче, где левая чашка — точно такая же, а правая совсем простая — тот же контейнер с водой, из которого просто убрали шарик. Количество воды в обеих чашках одинаково, но левую чашку — как предлагаете смотреть вы — «дополнительно тащит вверх натянутая всплывающим шариком нитка, а правую - нет.» Получается, что и в этом случае правая перевесит, хотя в реальности они в равновесии.
-
Количество воды одинаковое, но уровень будет разный. Соответственно, будет разное давление воды на дно, и простые рассуждения об одинаковой силе давления воды в обеих чашках более не проходят. Да, тут, конечно, приходится разбивать систему на части и замечать, что по вертикали вода давит только на дно, но не на стенки. С другой стороны, педагогически тут тоже есть полезность: используется то, что давление воды зависит только от глубины под её свободной поверхностью, но никак не зависит от того, что и где еще погружено в эту воду.
-
А, теперь дошло и до меня :) Вы смотрите не на вес, а на давление воды в сосуде с «внутренним сферическим иъзяном», и используете при этом то свойство, то этот сферический изъян в одном случае механически связан с сосудом, а в другом — нет. Это оригинально, да, но это своеобразное переписывание силы архимеда (т.е. силы, которая этот изъян удерживает в неподвижности, несмотря на силу архимеда). Как второе решение оно мне нравится, но как первое — я не уверен, что оно удобное для человека, для которого эта задача представляет существенную трудность.
-
Вас в первую очередь заботит педагогика, причем, в расчета на слабого школьника, а меня - красота решения. Понятно, что такие простые школьные задачи можно решать совершенно разными способами. И всегда обнаружение в задаче симметрии, позволяющей обойтись без вычислений, считалось законным и красивым решением.
Так вот, в моём решении вообще нет силы Архимеда в явном виде. Я говорю, что не важно, что там в воде болтается. По определению, вес тела - это сила, с которой тело действует на опору или подвес. В данном случае его можно оценить прямо через давление воды на дно сосудов, которое оказывается одинаковым и сокращается. Рассматривая только стенки сосуда и не заглядывая в глубины. Плюс сила натяжения нитки слева, для объяснения которой, действительно, нужно вспомнить закон Архимеда. Но так как у нас больше ничего не осталось, нам достаточно заметить, что эта сила положительна, так как шарик всплывает, и считать её величину тоже не нужно.-
Я всё же продолжу разговор :)
> ... нам достаточно заметить, что эта сила положительна, так как шарик всплывает, и считать её величину тоже не нужно.
Ну, в моем методе ее тоже считать не нужно, надо просто знать, что она есть, так что здесь разницы в методах нет. Но в вашем методе есть одна вещь, которая мне (опять же, педагогически!) не нравится.
> По определению, вес тела - это сила, с которой тело действует на опору или подвес.... Рассматривая только стенки сосуда и не заглядывая в глубины.
Давайте возьмем L-образный сосуд с высоким и тонким каналом и большой нижней площадью. Поставим себя на место ученика, которому эти задачи представляют некоторую трудность. Он познакомился с вашим методом и хочет применить его к этой системе для определения веса. Поскольку тут и уровень воды высокий и площадь дна большая, он перемножит давдение на площадь и получит огромный вес, намного превышающий вес воды. Он попадает в тупик, и лично я не представляю, как он из него сможет сам выпутаться. Для этого ему потребуется понять, что либо (1) ему надо считать интеграл по всей внутренней поверхности сосуда, находящейся в контакте с водой, от давления помножить на вектор нормали, и тогда львиная доля силы сократится, и останется только сила тяжести, либо (2) ему надо считать опорой не сосуд, а чашку весов, на которой он стоит с водой, но тогда нет пользы от разделения на сосуд и воду.
Так что, по-моему, ваш метод, примененный к такой системе, еще сильнее сбивает с толку человека, для которого эта задача была неэлементарной.
Я поясню, почему я вообще придираюсь. Понятно, что если есть решение, которое в любой конкретной задаче дает короткий и красивый путь к ответу — это всегда хорошо. Но иногда бывает, что красивое решение годится только для очень узкого класса ситуаций, а если его применять пошире, то возможны ошибки или усложнения. Поэтому опять же с педагогической точки зрения _обучать_ нужно этому методу, а такому, который позволяет _опираться_ на него в широком классе ситуаций. Предложенное мной решение — такого типа; ваш же метод содержит в себе дополнительные подводные камни.
-
-
-
-
Правильный ответ: прыгающие шарики легче неподвижных. Это следует из вычислений усредненной по периоду силы давления создаваемой прыгающим шариком. Для простоты будем полагать что коромысло весов зафиксировано; на окончательный вывод это упрощение не повлияет: если средняя сила окажется больше веса шарика, то левая чаша перевесит когда коромысло отпустят и наоборот. Изменение импульса шарика при абсолютно упругом отскоке от покоящейся чаши dp = 2*m*v, где v -- скорость шарика непосредственно перед ударом (после отскока). Период колебаний шарика T = время полёта + время отскока = t0 + t1 = 2*v/g + t1. Усреднённая за период сила давление на чашу F = dp/T = 2*m*v/(2*v/g + t1) = mg/(1 + t1*0.5*g/v) = mg/(1 + t1/t0). Как мы видим, в силу того что время отскока t1 конечно (хотя и очень мало по сравнению со временем полета t0), знаменатель больше единицы ==> F < mg ==> прыгающий шарик легче неподвижного.
Теперь задачку можно слегка усложнить: пусть шарики прыгают на обоих чашах весов, только на левой выше чем на правой. Какая чаша перевесит?
Последние задачи















Рис. 1. Четыре задачи на тему «Какая чашка весов перевесит?»; пояснения к условиям см. в тексте