Три уловки для мудрых
Задача
Не верьте, что 1 апреля — День Дурака! Ведь только от вас зависит, дадите ли вы себя одурачить. А мы предложим вашему вниманию три софизма (греч. Sophisma — ‘уловка’, ‘головоломка’ — восходит к имени Sophia, означавшему мудрость). В каждом из них доказывается очевидно неверное утверждение. Ваша задача — не просто сказать «этого не может быть, потому что не может быть никогда», а найти то место в доказательстве, в котором мы сознательно допустили ошибку.
Софизм первый. Углы тупыми не бывают.

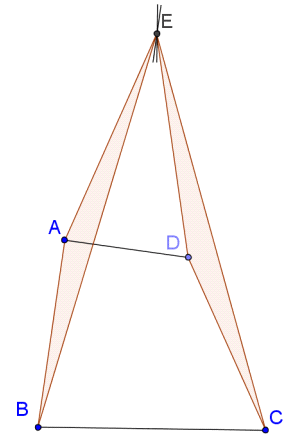
Здесь изображён четырёхугольник ABCD, у которого AB = CD, углы B и C — острые, а угол BAD — прямой. Как несложно увидеть из рисунка (или доказать, воспользовавшись тем, что сумма углов равна 360°), угол ADC тупой. Проведём серединные перпендикуляры к AD и BC до их пересечения в точке E. Тогда по свойству серединного перпендикуляра AE = DE и BE = CE. Поэтому треугольники ABE и DCE равны по трём сторонам. Следовательно, равны и соответствующие углы: ∠BAE = ∠CDE. Но так как AE = DE, то треугольник AED равнобедренный, поэтому углы при его основании равны: ∠ADE = ∠DAE. Тогда получим, что ∠ADC = ∠CDE – ∠ADE = ∠BAE – ∠DAE = ∠BAD. Итак, тупой угол равен прямому, то есть 90°.
Софизм второй. Квадратное уравнение имеет три корня.
На сей раз попробуйте разоблачить «ловкость рук» в школьной алгебре. Как известно, квадратное уравнение может иметь либо два корня, либо один, либо вообще не иметь корней. Но так ли это на самом деле? Посмотрите на вот это уравнение:
Здесь a, b, c — любые различные числа. Поскольку в числителе каждой дроби перемножаются две скобки, содержащие x, то это уравнение, несомненно, является квадратным. Однако подставим в него x = a: первое слагаемое станет равно 1, а второе и третье содержат множитель (x – a), поэтому обратятся в 0. Таким образом, при x = a получается равенство 1 = 1, то есть x = a — корень этого уравнения. Совершенно аналогично проверяется, что x = b и x = c тоже являются корнями. Значит, это уравнение имеет три различных корня.
Софизм третий. 1 = 0.
Настал черёд математического анализа. Рассмотрим бесконечную сумму (ряд):
Как известно, он сходится, и его сумма равна 1 (см. Телескопический ряд), потому что его слагаемые можно представить в виде:
и все слагаемые, кроме самого первого, сократятся, то есть останется только 1/1. Итак, запишем:
Перенесём первое слагаемое в левую часть и перепишем результат в виде:
Повторим многократно эту же операцию, учитывая, что 1/2 – 1/(2·3) = 1/3, 1/3 – 1/(3·4) = 1/4 и т. п.:

и так далее. Теперь сложим все полученные равенства, одновременно сокращая все равные слагаемые. Тогда 1/2 сократится с 1/(1·2), 1/3 сократится с двумя дробями 1/(2·3), 1/4 — c тремя дробями 1/(3·4), и так далее. Каждое слагаемое 1/(n·(n + 1)) встречается в правой части в первых n равенствах, поэтому сумма таких слагаемых равна 1/(n + 1), и она сократится с левой частью (n + 1)-го равенства. Таким образом, в правой части равенства не останется ничего. Ну а в левой части останется единица, которой точно не с чем сокращаться. Таким образом, мы доказали, что 1 = 0.
Подсказки 1
1. Треугольники ABE и CDE действительно должны быть равны (рисунок намеренно сделан ошибочным, но ошибка не в этом месте).
2. Числа a, b, c — действительно корни этого уравнения. И они действительно различны.
3. Каждое из равенств само по себе ошибки не содержит.
Подсказки 2
1. Равные треугольники неправильно изображены на рисунке.
2. Не всё, что содержит переменную x, является уравнением!
3. Фактически мы пытаемся сложить бесконечное число равенств. Всегда ли результат таких действий будет верным равенством?
Решения
1. Правильная картинка выглядит примерно вот так:
Обратите внимание на то, как ориентированы два треугольника. Углы EAD и EDA действительно равны, углы EAB и EDC тоже равны, но ни к каким противоречиям это не приводит. В одном случае мы вычитаем меньший угол из большего и получаем прямой угол BAD, а в другом — нужно, наоборот, сложить два угла и вычесть сумму из 360°, чтобы в результате получить тупой угол ADC. Различные действия закономерно приводят к разным результатам, ничего странного (а тем более, противоречащего здравому смыслу) тут нет.
2. Ошибка в том, что мы назвали квадратным уравнением то, что всего лишь выглядит как квадратное уравнение. На самом же деле решения этого уравнения — не только числа a, b и c! Его корнем является любое действительное число (если немного потрудиться, раскрыть скобки и привести подобные слагаемые, то получится 0x2 + 0x + 1 = 1). Иными словами, это не квадратное уравнение, а тождество, и опять-таки нет ничего странного в том, что при подстановке в него трёх разных чисел получаются верные равенства.
3. Ошибка — именно в попытке сложить бесконечное число верных равенств. Если бы сумма 1 + 1/2 + 1/3 + 1/4 + 1/5 + ... существовала, то такая попытка, скорее всего, привела бы к верному результату. Однако такой ряд расходится (см. Гармонический ряд), поэтому попытки как-то оперировать с его суммой и отдельными слагаемыми (например, переставлять их местами, что необходимо для того, чтобы сложить несколько равных дробей из разных строчек) могут приводить к неверным результатам. Что, собственно, с нами и произошло.
Послесловие
Софизмы и парадоксы — любимый «конёк» специалистов по логике, которые обожают таким образом демонстрировать мнимую парадоксальность обыденных вещей. Некоторые из сюжетов специально формулируются в шутливом стиле. Например, Крокодил или Парадокс всемогущества.
Но наши задачки всё же немного о другом.
Геометрический софизм — не более чем разминка для мозгов, заодно служащая напоминанием о том, как сложно построить что-то основательное на шатком фундаменте. Вся геометрия с её теоремами и доказательствами выросла из желания людей не доверять плохому чертежу, а иметь более строгие обоснования. Тем не менее даже изучавших геометрию плохие чертежи запросто вводят в заблуждение, не так ли?
Задача про квадратное уравнение с тремя корнями имеет намного более глубокие связи с «настоящей» математикой. Левая часть выписанного «квадратного уравнения» — не что иное, как интерполяционный многочлен Лагранжа — конструкция многочлена минимальной степени, принимающего данные значения в заданном наборе точек. А именно, мы построили многочлен, который принимает значение 1 в точках a, b, c.
Кроме прямого назначения (для решения задач интерполяции, то есть нахождения приближённого значения функции в произвольной точке), такие многочлены используются и в других разделах математики, например в прикладной криптографии (см. Схема Шамира).
Но с исторической точки зрения, конечно, наибольшее влияние на развитие математики оказали «фокусы с бесконечностью», один из которых мы продемонстрировали в третьем софизме. Несмотря на то что рассуждения о бесконечно малых величинах можно найти ещё у древних греков (Аристотеля, Архимеда и Демокрита), а современным дифференциальным исчислением мы обязаны Исааку Ньютону (1642–1727) и Готфриду Вильгельму Лейбницу (1646–1716), ещё более сотни лет после Ньютона и Лейбница математики продолжали натыкаться на парадоксы и противоречия при переходах к пределу, а тем более — при суммировании бесконечных рядов. Понадобились гений Леонарда Эйлера (1707–1783) и педантичность Огюстена Луи Коши (1789–1857), прежде чем эта часть математического здания оказалась выстроенной надёжно и прочно (см. Сходимость).
-
Не нравится мне такая фраза в №3: " Ошибка — именно в попытке сложить бесконечное число верных равенств". Есть правильно складывать, никакой ошибки быть не должно.
Сложим n равенств. Тогда со слагаемым 1/n в левой части сократятся n-1 слагаемых в правой части, которые имеют вид 1/(n-1)*n. Итого в левой части останется 1, а в правой - слагаемые, начиная с 1/n*(n+1), их будет n штук.
1=n*(1/n(n+1)+1/(n+1)(n+2)+...)
Сумму в скобках мы находим по формуле ряда:
1/n(n+1)+1/(n+1)(n+2)+...=(1/n-1/(n+1))+(1/(n+1)-1/(n+2))+...=1/n
Итого 1=n*1/n-
Вроде бы там довольно ясно написано, что нельзя оперировать с отдельными слагаемыми рядов, которые не сходятся равномерно.
Ваш подход иллюстрирует этот факт. Есть два вполне логичных способа суммирования, один в статье, другой у вас. Они дают два разных результата. А так быть не должно.
Известный пример, когда подобный подход приводит к двум разным результататм -- это ряд 1-1+1-1+1-1+... Если складывать так: (1-1)+(1-1)+..., то получится ноль. А если так: 1-(1-1)-(1-1)-..., то будет 1.
Именно поэтому и развивали люди теорию рядов. Чтобы получить универсальный метод, который работает всегда одинаково.
-
Последние задачи














