Школьники пишут тест

Подумайте, какое наибольшее количество учеников могли выбрать ответ (а) в первом задании теста.

Воспользуемся рассуждением, которое в математике носит специальное название «принцип Дирихле» и в полушуточной формулировке обычно звучит так: если более четырех кроликов посадить в четыре клетки, то найдется клетка, в которую посажены не менее двух кроликов.

Это рассуждение помогает сразу ответить на вопрос из подсказки 1. Если бы учеников, давших ответ (а) на первое задание, было больше четырёх, то у каких-то двух из них по принципу Дирихле совпали бы ответы и на второе задание теста (потому что различных вариантов ответа там всего четыре), а значит, совпали бы ответы в двух заданиях. Условие задачи это явно запрещает.

Как следует из объяснений в подсказках, каждый вариант ответа в каждом задании дали ровно четыре ученика. Выберем любого из учеников, например, Васю Пупкина. Его ответ на первое задание совпал с ответами каких-то трех других учеников. Ответ Васи на второе задание совпал с ответами тоже каких-то трех учеников. Причем все они не входили в первую тройку! (Иначе у Васи и входившего в обе тройки ученика были бы одинаковые ответы на два задания — первое и второе.) Аналогично, ответ на третье задание дает еще одну тройку учеников, и т. д. Поскольку всего остальных учеников 15, а по каждому заданию с Васей совпадали новые трое, то заданий могло быть не более пяти.

Мы получили оценку, показывающую, что тест не мог состоять более чем из пяти заданий. Но это еще не всё. Вдруг наша оценка неточна, и тест из пяти заданий тоже не удастся написать так, чтобы выполнялись условия задачи?

Как ни крути, приходится строить пример... Я мог бы ограничиться выписыванием готового ответа, но хочу показать в деталях механизм рассуждения, которое к этому ответу приводит.

Начнем с построения списка ответов для первой четвёрки учеников. Будем обозначать выбор первого варианта ответа цифрой 1, второго — 2, третьего — 3, четвертого — 4.

Четырем ученикам, у которых совпали ответы на первое задание, мы можем совершенно свободно дописать по всем остальным заданиям одинаковые цифры ответов.

11111
12222
13333
14444

Почему это так? Потому что ответы на разные задания совершенно независимы, и мы можем считать, что варианты, выбранные вторым учеником в каждом из заданий 2–5, стояли там вторыми (а если это было не так, то их всегда можно было на вторые места переставить, соответственно поменяв номера ответов у всех учеников). Аналогично, третьему ученику достались третьи варианты, а четвёртому — оставшиеся, то есть четвёртые.

Теперь у нас остались еще 12 учеников. Ответы на первое задание разбили их на 3 группы по 4 (четверо дали ответ «2», четверо - «3», четверо - «4»). Назовём эти группы «блоками». Что мы можем сказать про их ответы на следующие задания теста? С каждым из первой четвёрки они должны иметь общий ответ ровно один раз. Это значит, что у каждого ученика в списке ответов на задания 2–5 встречается ровно одна единица, одна двойка, одна тройка и одна четвёрка. Кроме того, каждая пара учеников из одного блока должна иметь не более одного общего ответа, и этот ответ у нее уже определён (на первое задание). Таким образом, ответы на задания 2–5 должны различаться не только в строках, но и столбцах. Таким образом, мы получаем, например, для второго блока без первого столбца магический квадрат:

2 1234
2 2143
2 3412
2 4321

Понятно, что для третьего и четвёртого блоков тоже должны получаться магические квадраты. Выстроим их так, чтобы единички стояли вдоль диагоналей (это достигается простой перестановкой строчек, поскольку в каждой строчке и каждом столбце есть ровно одна единичка).

3 1   
3   1  
3     1 
3       1

4 1   
4   1  
4     1 
4       1

Теперь поймём, какими должны быть остальные ответы у первых учеников из трех разных блоков:

2 1234
3 1   
4 1   

У них совпадают ответы на второе задание — значит, никакие другие совпасть не должны. Это означает, что цифры 2, 3, 4 в этих трех строчках также должны заполнить магический квадрат:

21 234
31 342
41 423

Аналогичный квадрат должен получиться и для вторых учеников из трёх блоков. Но какой из двух возможных квадратов мы должны выбрать — этот:

2 2143
3 4132
4 3124

или вот этот:

2 2143
3 3124
4 4132

Чтобы ответить на этот вопрос, посмотрим на ученика из предыдущей тройки с ответами 31342. С ним конфликтует ответ 34132, но не конфликтует ответ 33124. Следовательно, мы должны выбрать второй вариант магического квадрата, и таким образом, сейчас у нас заполнена следующая часть таблички ответов:

11111
12222
13333
14444

2 1234
2 2143
2 3412
2 4321

3 1342
3 3124
3     1 
3       1

4 1423
4 4132
4     1 
4       1

Теперь уже более-менее понятно, как можно заполнить до конца табличку, вписывая цифры:

Последние цифры вписаны с оглядкой на строчки «23412» и «24321». Например, первая из них уже имеет общую единицу в четвертом столбце со строчкой «3__13», поэтому 2 и 4 вписываются в эту строчку как 42, а не как 24. Аналогично, 2 и 3 вписываются в «4__41» как 32, а не как 23.

Итого, мы построили такой пример ответов на тест для 16 учеников.

11111
12222
13333
14444

21234
22143
23412
24321

31342
33124
34213
32431

41423
44132
42314
43241

Из построения примера понятно, что он удовлетворяет нужным условиям для таких пар учеников:
– два ученика из одного блока (у них совпадают ответы на задание 1);
– один ученик из первого блока, другой — из какого-то другого (у них совпадают ответы, равные номеру блока).

Несложно проверить, что и для остальных пар учеников условия задачи тоже выполнены.

Пожалуй, самое удивительное в этой задаче то, что математики относят ее к геометрии, а не к алгебре. Точнее, область, к которой она относится, называется «конечные геометрии» и лежит на стыке геометрии и комбинаторики.

В конечных геометриях, как и в обычных геометриях (и евклидовой, и Лобачевского), имеется своя система аксиом, на основании которых выводятся различные (подчас очень непростые) теоремы.

«Точками» обычно называют элементы любого непустого множества, а «прямыми» — некоторый набор подмножеств этого множества. При этом должны быть выполнены такие аксиомы:

1. Для двух различных точек существует и единственна содержащая их прямая
2. Для любой точки M и любой не содержащей ее прямой m существует ровно одна прямая m', содержащая эту точку и не имеющая общих точек с m. (Правда, логично назвать такую прямую параллельной? Обычно так и делают, хотя геометрически параллельность прямых m и m' на картинках, изображающих конечные геометрические конфигурации, вовсе не обязательна — главное, чтобы эти прямые не пересекались в точке, принадлежащей заданному множеству!)
3. Существуют четыре точки, никакие три из которых не лежат на одной прямой.

Пример относительно несложной теоремы: каждая прямая содержит одно и то же количество точек.

Простейшая конечная плоскость содержит всего 4 точки и идеально иллюстрирует упрощение нашей задачи для четырех учеников и двух вариантов ответа на каждую задачу.

Конструкция для такой упрощенной версии почти очевидна — один из учеников должен выбрать везде первые варианты ответов, а каждый из остальных учеников даёт только один первый вариант и два вторых:

111
122
212
221

Как это переводится на язык «точки-плоскости»? Очень просто. Назовём точками учеников, а прямыми — те подмножества, в которых все ученики дали один и тот же ответ на одну и ту же задачу. Прямых получилось всего 6 (1 + 2 и 3 + 4 — по первой задаче, 1 + 3 и 2 + 4 по второй, 1 + 4 и 2 + 3 по третьей), и в точном соответствии с последней аксиомой среди этих прямых есть параллельные — а именно, те пары прямых, которые соответствуют одной и той же задаче.

Эту конфигурацию можно изобразить на картинке. Вот, например, как это сделано в «Википедии»:

Рисунок конечной плоскости, которая содержит 4 точки и 6 прямых. «Прямые» одного цвета являются «параллельными». Из статьи Конечная геометрия

Говорят, что такая конечная плоскость имеет порядок 2 — по числу точек, лежащих на одной прямой.

Аналогичная картинка есть и для плоскости порядка 3 (на ней 9 точек):

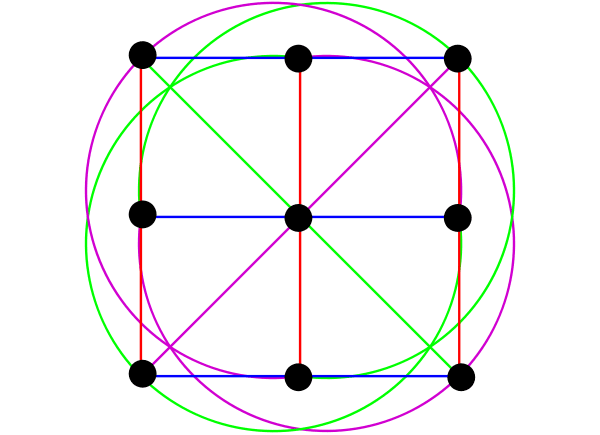
Графическая иллюстрация конечной плоскости третьего порядка, содержащей 9 точек и 12 прямых. «Прямые» одного цвета являются параллельными в том смысле, что пересечение множества точек в двух прямых одного цвета является пустым. Из статьи Конечная геометрия

Ну а теперь «раскроем секрет» — о чём же была наша задача? В ней спрашивалось, какое число «направлений» содержит конечная плоскость порядка 4. Под направлением мы понимаем любое множество попарно параллельных прямых (по третьей аксиоме, такие прямые точно существуют, а вторая аксиома говорит о том, как они должны быть устроены).

Получение оценки в задаче фактически сводится к трем простым фактам: на каждой прямой лежит по четыре точки, поэтому каждое направление состоит из 16/4 = 4 прямых. А так как через каждую пару точек можно провести прямую, то легко сосчитать и число прямых, проходящих через фиксированную точку: каждая из 15 остальных точек лежит на какой-то прямой, причем на каждой такой прямой лежат по три точки, поэтому прямых всего 15/3 = 5.

Ну а число прямых, проходящих через каждую точку, — это и есть число направлений, потому что среди этих прямых нет двух параллельных, и для любой другой прямой среди этих прямых по аксиоме 2 найдется одна им параллельная.

Построенный нами пример фактически даёт способ построения конечной плоскости порядка 4.

Несмотря на всю простоту аксиом и примеров, в конечных геометриях есть масса нерешенных (открытых) задач. Наиболее важная из них, пожалуй, такая:

Обязательно ли порядок конечной плоскости — степень простого числа?

Большинство математиков предполагает, что это так, но никаких подходов к доказательству не найдено. Все конструкции для тех случаев, когда порядок плоскости является степенью простого числа, известны, так что фактически проблема сводится к несуществованию плоскостей других порядков.

Частичный ответ даёт теорема Брука-Райзера:
Если n — натуральное число, дающее при делении на 4 остатки 1 или 2 и не представимое в виде суммы двух квадратов, то n не является порядком конечной плоскости.

Наименьшим числом, для которого эта теорема не давала ответа на вопрос о существовании конечной плоскости, долгое время было 10 (оно даёт остаток 2 при делении на 4, но представимо в виде суммы квадратов: 1 + 9). Отсутствие конечной плоскости порядка 10 было доказано (с помощью компьютера, куда ж без него) только в 1989 году.