Скорость радиально поляризованного света

Рис. 1. Радиально поляризованный свет в поперечной плоскости. Цветом показана интенсивность светового поля, стрелочки — вектора электрического поля в разных точках плоскости. Изображение из статьи Optics Express, 7, 77-87 (2000)

Скорость света в вакууме, обозначаемая латинской буквой c, — это одна из самых важных физических констант. Всем хорошо известно, что световой луч летит в вакууме именно с такой скоростью, какова бы ни была его интенсивность или длина волны. На самом деле это утверждение не совсем верно. Свет движется со скоростью строго равной c только в том случае, если он представляет собой бесконечную во всех направлениях плоскую волну (что это такое, пояснено ниже). Но настоящих плоских волн в природе не бывает, поэтому скорость реального светового луча в вакууме неизбежно отличается от c. В большинстве случаев, если расходимость светового пучка невелика, это отличие очень мало, и заметить его трудно. Однако можно создать такой пучок света, в котором отличие будет существенным. В этой задаче как раз и предлагается найти скорость распространения специального светового пучка с цилиндрической симметрией.

Бегущая плоская монохроматическая волна
(Справочный материал)

Для начала надо рассказать, как описывается бегущая волна. Вообще, волна — это колебание (то есть периодическое уменьшение и увеличение) какой-то величины, которое распространяется в пространстве (рис. 2). В случае света колеблются электрическое и магнитное поля, в случае звуковой волны колеблется плотность среды, в случае волны на воде колеблется уровень жидкости. Обозначим эту колеблющуюся величину через a и будем для простоты считать, что она колеблется относительно нуля.

Рис. 2. Характеристики плоской монохроматической волны. Слева: одномерная волна в разные моменты времени, справа: двумерная волна и направление волнового вектора

У всякой волны есть два типа периодичности — во времени и в пространстве. Для простейшей волны зависимость колеблющейся величины от времени в какой-то фиксированной точке пространства выражается таким законом: a(t) = A cos(ωt), где A — это амплитуда волны, а ω — ее частота. Период колебаний связан с частотой: T = 2π/ω. Если же, наоборот, зафиксировать момент времени, то у волны будет пространственная периодичность, которая выражается такой формулой: a(r) = A cos(k·r). Все жирные буквы обозначают трехмерные вектора: r — это вектор координат, k — это так называемый волновой вектор, а k·r — их скалярное произведение. Волновой вектор — это характеристика волны, показывающая ее пространственную периодичность, как бы пространственный аналог частоты. Направление вектора k показывает, в какую сторону смотрят «гребни волн», а длина волны связана с модулем этого вектора: λ = 2π/k.

Если мы хотим получить бегущую волну, движущуюся в направлении вектора k, надо записать и координатную, и временную зависимость: a(r, t) = A cos(k·r – ωt). Всё выражение, которое тут стоит под косинусом, называется фазой волны. Эта формула описывает монохроматическую плоскую волну. «Монохроматическая» означает, что у нее фиксированная частота (то есть «цвет»), а «плоская» означает, что поверхности одинаковой фазы представляют собой плоскости, перпендикулярные волновому вектору.

Чтобы найти скорость плоской монохроматической волны, сделаем небольшое преобразование внутри косинуса:

a(r, t) = A cos(k·r – ωt) = A cos[k(r – vt)].

Вектор v направлен вдоль k, а его модуль равен v = ω/k. Благодаря выражению r – vt видно, что v и является скоростью волны (а точнее, фазовой скоростью): с течением времени весь фронт волны смещается вперед как раз с такой скоростью. В принципе, v может зависеть от ω; это явление называется дисперсией. Но для света в вакууме эта скорость всегда по модулю равна с для любой частоты. Именно поэтому и утверждается, что скорость света в вакууме — константа.

Важное свойство волн состоит в том, что их можно накладывать друг на друга. Если волна «не мешает сама себе» (в физической терминологии — волна линейная), то отдельные волны будут просто проходить друг сквозь друга без взаимодействия. Например, выражение

a(r, t) = A₁ cos(k₁·r – ω₁t) + A₂ cos(k₂·r – ω₂t)

описывает две наложенные друг на друга волны с разными амплитудами, частотами и волновыми векторами. Если частоты совпадают, а направления волнового вектора — нет, то волна будет по-прежнему монохроматической, но уже не плоской. Разумеется, можно также накладывать друг на друга не только две, но и больше волн, и даже бесконечное их число.

Перейдем теперь непосредственно к задаче и построим специальный пример неплоской электромагнитной волны, известной под названием радиально поляризованный свет. Для этого выберем ось z и наложим друг на друга бесконечное число монохроматических плоских волн одинаковой частоты и амплитуды, бегущих под углом α к оси z. Волновые вектора всех этих волн одинаковы по модулю, но отличаются азимутальными направлениями. В декартовой системе координат волновой вектор любой из этих плоских волн запишется так:

k = k(cosφ·sinα, sinφ·sinα, cosα),

где угол α фиксирован, а азимутальный угол φ — переменный, он как раз характеризует, в каком направлении бежит каждая конкретная плоская волна в этом семействе волн. Наконец, для каждой плоской волны зададим поляризацию так: волна линейно поляризована и вектор электрического поля лежит в плоскости, заданной вектором k и осью z. И последний штрих: будем считать, что все волны скоординированы по фазе, то есть в точке r = 0 и в момент времени t = 0 у всех у них одинаковая нулевая фаза. Рис. 3, на котором волновые вектора заметают поверхность конуса, должен помочь визуализировать это построение.

Рис. 3. Световой пучок, состоящий из набора всевозможных плоских волн, волновые вектора которых подходят под углом α к оси z. Синими стрелками показаны волновые вектора некоторых из плоских волн, красным цветом — вектора электрического поля для пары волн, чьи волновые вектора лежат в плоскости (x, z)

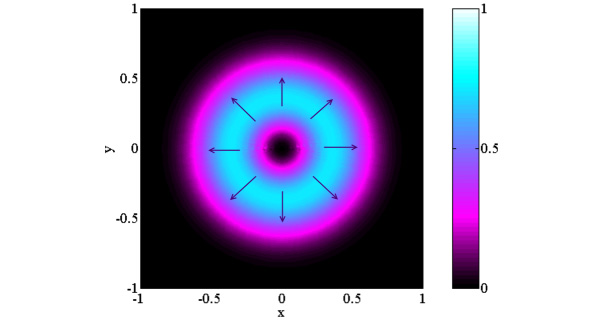
Радиально поляризованным такой световой пучок называется потому, что, если его спроецировать на поперечную плоскость, вектора электрического поля будут торчать «ежиком», вдоль радиального направления (рис. 1).

Решение

Следуя подсказке, выбираем две волны с противоположными углами φ и записываем суммарное электрическое поле:

Затем используем формулу для косинуса суммы и разности углов

cos(a + b) = cos a·cos b – sin a·sin b,
cos(a – b) = cos a·cos b + sin a·sin b,

и получаем

Обратите внимание, что периодичность по оси x — стоячая, она никуда не бежит. Время входит только в тот косинус и синус, в котором содержится координата z. Это значит, что наложение двух таких плоских волн порождает волну, бегущую строго вдоль оси z. Фазовую скорость этой суммарной волны легко найти из определения:

v = ω/(k·cosα) = c/cosα.

Заметьте, что фазовая скорость такой волны оказалась больше скорости света c.

Этот результат никак уже не зависит от ориентации оси x и годится для любой пары волн с противоположными углами φ из нашего семейства. Поэтому, просуммировав все эти пары, мы наложим друг на друга бесконечное число волн, бегущих вдоль оси z с одинаковой скоростью c/cosα. Таким образом, и полная суммарная волна тоже бежит вдоль оси z с той же сверхсветовой фазовой скоростью.

У этой волны будет некоторое нетривиальное распределение в поперечной плоскости, которое, впрочем, будет обладать цилиндрической симметрией (то есть оно не изменится при повороте на любой угол вокруг оси z). Но для нашей задачи это распределение несущественно.