Бинарный сплав
Многие вещества в твердом состоянии образуют кристаллическую решетку, причем атомы или ионы разных типов, составляющие это вещество, чередуются в ней строго определенным образом. Всем известный со школы пример кристалла — поваренная соль NaCl — имеет кубическую решетку, в узлах которой сидят ионы натрия и хлора. У каждого иона натрия ближайшие соседи — только ионы хлора, у каждого иона хлора соседи — ионы натрия. Так получается потому, что ионы натрия и хлора притягиваются друг к другу, а два иона хлора или два иона натрия расталкиваются.
Однако далеко не всегда взаимное расположение атомов или ионов в решетке настолько жестко задано. Например, в металлических сплавах силы притяжения между ионами одного металла или разных металлов могут оказаться примерно одинаковыми. Сплав также образует кристаллическую решетку, но как именно ионы разных металлов рассядутся по ее углам — заранее не понятно.
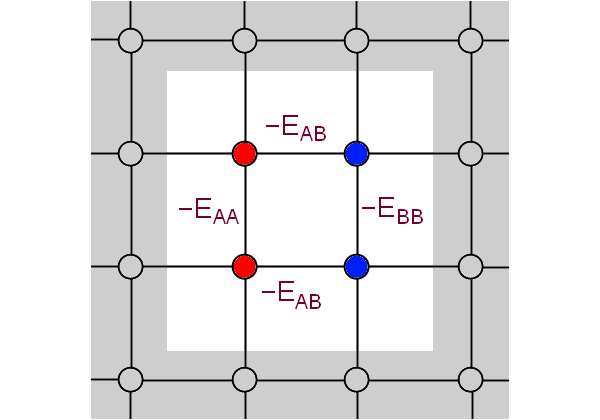
Рассмотрим простейшую модель бинарного сплава (то есть сплава из двух металлов), см. рис. 1. Пусть для простоты кристаллическая решетка будет двумерной и квадратной. В узлах этой решетки как-то расположены ионы типа A и типа B, причем их в кристалле поровну. Будем считать, что каждый ион «чувствует» только четыре ближайших соседних иона, причем потенциальные энергии взаимодействия в каждой паре известны: два соседних иона типа A взаимодействуют с энергией –EAA, два иона типа B — с энергией –EBB, а два иона разного типа — с энергией –EAB. (Величины EAA, EBB, EAB положительны, а знаки «минус» означают, что потенциальная энергия между ионами отрицательна, то есть она способствует их притяжению.)
Задача
Как именно рассядутся ионы A и B по узлам решетки при низких температурах?
Подсказка 1
Низкая температура означает, что можно не учитывать тепловые флуктуации, которые могут привести к случайным перескокам ионов из одного узла в другой. После того как у кристалла отобрали всё тепло, он застынет в состоянии, отвечающем минимуму потенциальной энергии. Поэтому надо разобраться, какое именно расположение ионов типа A и B по кристаллу сможет минимизировать его общую потенциальную энергию при заданных значениях EAA, EBB и EAB.
Подсказка 2
Если сходу непонятно, как именно они должны сидеть в решетке, нарисуйте какое-нибудь простое расположение ионов так, чтоб ионов A и B было поровну, и сосчитайте, какая потенциальная энергия приходится в среднем на один узел. Попробуйте понять, что нужно для того, чтобы минимизировать эту величину.
Подсказка 3
На всякий случай стоит уточнить, что краевыми эффектами (то есть тем фактом, что в куске металла самые крайние ионы имеют связи, торчащие наружу) можно пренебрегать. Дело в том, что обычно рассматривается макроскопический кусок вещества, а в нём таких граничных ионов намного меньше, чем ионов в толще материала, и потому эффект от них очень мал.
Решение
Интуитивно понятно, что если EAA и EBB велики, а EAB — нет, то ионам одного типа энергетически выгодно держаться вместе. Наоборот, если EAB будет очень большой, то каждому иону выгоднее иметь всех соседей противоположного типа. В результате мы приходим к двум решеткам-кандидатам, показанным на рис. 2.

В первой решетке все связи типа AB, во второй — половина связей связи типа AA, половина — типа BB. (Граница раздела между двумя половинками металла содержит связи AB, но их на много порядков меньше, чем связей в толще вещества, и подобными граничными эффектами мы договорились пренебрегать.) Поэтому первая решетка становится выгоднее второй при выполнении условия:
2EAB > EAA + EBB.
В обратном случае энергетически более выгодной является вторая решетка — то есть полное разделение сплава на два несмешивающихся металла.
На самом деле, сравнение двух конкретных решеток — это еще не решение задачи. Ведь всего вариантов расположения ионов в решетке огромное множество, и все их перебирать и сравнивать друг с другом невозможно. Нужно найти способ, который доказал бы, что никакие другие решетки не могут быть еще более выгодными.
Для этого придется сделать чуть более сложные вычисления. Пусть у нас есть N ионов сорта A и N ионов сорта B. Полное количество узлов решетки 2N, а полное количество парных связей 4N. В произвольном расположении ионов по решетке будут связи всех трех типов: AA, BB, и AB; их количество обозначим как NAA, NBB и NAB, и вместе они должны давать 4N.
Между этими числами есть и еще одна связь. Рассмотрим какой-то определенный ион типа A. Всего из него выходит четыре связи, nAA штук типа AA и nAB штук типа AB: nAA + nAB = 4. Просуммируем теперь по всем ионам типа A, которых N штук. При этом все связи AA у нас сосчитаются ровно по два раза, все связи AB — ровно по одному разу, и никаких несосчитанных связей AA или AB у нас не останется. Это дает 2NAA + NAB = 4N. Аналогичное выражение получится и для ионов сорта B. Вычитая из одного другое, получим NAA = NBB.
Итак, среди трех чисел NAA, NBB и NAB есть только одно независимое, а остальные выражаются через него. В качестве независимого выберем, например, NAB и запишем его так: NAB = 4Nx. Величина x показывает, какую долю от всех связей составляют связи AB, и может меняться от 0 до 1. Тогда NAA = NBB = 2N(1 – x). Итак, величина x — единственная нужная для нас характеристика, описывающая состояние сплава.
Теперь всё готово для того, чтобы записать полную потенциальную энергию куска сплава:
–Etot = NAA EAA + NBB EBB + NAB EAB = 2N(EAA + EBB) + 2Nx(2EAB – EAA – EBB).
Минимум Etot получается, когда произведение x(2EAB – EAA – EBB) максимально. Если выражение в скобках больше нуля, то максимум достигается при x = 1. Но это означает, что все связи в кристалле — типа AB, а это возможно в единственном случае, показанном на рис. 2, слева. Если же выражение меньше нуля, то максимум достигается при x = 0. Это означает, что (за исключением граничных эффектов) в кристалле вообще нет связей AB, то есть что ионы двух типов не перемешиваются (рис. 2, справа). Итак, мы не только получили угаданный раньше ответ, но и доказали, что все бесчисленные промежуточные решетки, которым отвечают 0 < x < 1, никогда не будут энергетически более выгодными.
Послесловие
Описанная модель, несмотря на свою простоту, на самом деле очень богата на разные явления, которые возникают при малейшем усложнении задачи. Например, вы можете попробовать решить ту же задачу для случая, когда ионов одного сорта больше, чем другого, или же когда на той же решетке нужно рассадить ионы не двух, а нескольких разных сортов.
Но это всё математические комбинаторные усложнения. Вопросы, интересные с точки зрения физики, возникают при ненулевой температуре. Заметьте, что два полученных нами решения выглядят сильно по-разному, но имеют одну схожую черту — расположение ионов в решетке строго упорядочено. При повышении температуры этот порядок начнет постепенно стираться, и в некоторый момент происходит фазовый переход — порядок исчезает вообще и ионы начинают гулять по узлам решетки хаотично. На глаз такой кусок металла не отличишь от рис. 2, слева, но у него изменятся термодинамические характеристики, например теплоемкость. Такой фазовый переход «порядок—беспорядок» очень характерен для магнитных материалов.
Еще одно интересное замечание касается перестройки решетки при остывании изначально горячего куска сплава. Мы нашли наиболее выгодные кристаллические решетки при низких температурах. Но может оказаться так, что образец охладили так быстро, что его реальная структура очень сильно отличается от оптимальной. Конечно, с течением времени ионы будут потихоньку меняться местами так, чтобы оптимизировать потенциальную энергию. Но в холодном состоянии этот процесс может длиться так долго, что нам будет казаться, что сплав застыл в неоптимальном состоянии.
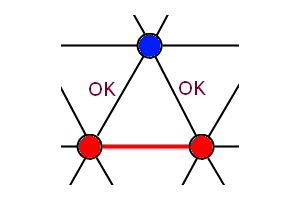
Наконец, последнее замечание касается формы решетки. Что изменится, если вместо квадратной решетки взять треугольную? Поразительное наблюдение заключается в том, что тогда решение в случае, когда связи AB сильны, поменяется принципиально! Дело в том, что из-за геометрии решетки у нас уже не получится сделать сразу все связи типа AB. На рис. 3 показан кусочек такой решетки: в выделенном треугольнике можно организовать лишь две связи AB, а третья неизбежно получится либо AA, либо BB. Такое «бессилие» решетки оптимизировать сразу все связи называется в физике фрустрацией.
Самое главное свойство систем с фрустрацией состоит в том, что в них нет какой-то единственной конфигурации, минимизирующей энергию. Таких конфигураций — огромное число, и они могут сильно отличаться друг от друга. (Кстати, попытайтесь нарисовать несколько примеров.) У фрустрированных систем бывают также и необычные флуктуации с экзотическими свойствами (недавно открытый пример — магнитные монополи в спиновом льду). Вообще, фрустрированные материалы остаются одной из самых горячих тем в современной физике конденсированных сред.
Последние задачи











