Закрученный свет шагнул на два порядка вверх по шкале энергий

Рис. 1. Волновой фронт для плосковолнового (в центре) и для закрученного света (слева и справа). Если раньше закрученный свет ограничивался лишь оптическим диапазоном, то сейчас его удалось получить и в рентгене. Изображение из обсуждаемой статьи в Phys. Rev. Lett.

Закрученный свет — необычная световая волна, несущая вращательный момент, — используется в физике уже давно, но до сих пор он не выходил за пределы оптического диапазона. Сейчас немецким физикам удалось получить яркий пучок закрученного рентгена с энергией фотонов 99 эВ. Это открывает новые возможности как в фундаментальной физике, так и для многочисленных приложений.

Закрученный свет: первое знакомство

Закрученный свет — это разновидность световой волны, у которой волновой фронт не плоский, а спиральный, словно винт с резьбой (рис. 1). Из-за такого нестандартного профиля пучок закрученного света не просто летит вперед, но еще и словно крутится вокруг направления своего движения. Такой световой луч несет не только энергию, импульс и поляризацию, но еще и определенное вращение, определенный орбитальный угловой момент.

Сразу стоит сделать важную оговорку: несмотря на то, что картинка на рис. 1 напоминает стандартную иллюстрацию для циркулярной поляризации, это две разные и независимые характеристики световой волны. Поляризация связана с направлением электрического поля в плоской волне, а закрученность характеризует волновой профиль неплоской волны неважно с какой поляризацией. Подробное объяснение см. в нашей статье Закрученный свет и закрученные электроны: обзор новых результатов.

То, что фотоны могут нести не только поляризацию, но и орбитальный угловой момент, было понятно уже давно. Но реальные узконаправленные световые пучки с винтовым волновым фронтом научились получать лишь в 1995 году. Благодаря огромному интересу технология получения, детектирования и управления закрученным светом быстро усовершенствовалась и буквально за одно десятилетие превратилась в рутинный метод исследований в самых разных разделах физики.

Здесь и тонкие вопросы оптики, как классической, так и квантовой, и разнообразные вопросы из квантовой теории информации. Квантовые состояния двух фотонов можно запутывать не только по поляризации (которая дает всего лишь двумерное пространство для запутывания, то есть произвольные комбинации правой и левой циркулярной поляризации), но и по орбитальному угловому моменту. А поскольку он может быть любым целым числом, то и пространство для манипуляций тут намного более емкое, формально оно сколь-угодно-мерное. Сейчас уже умеют запутывать состояния фотонов с орбитальным угловым моментом не ±1, не ±2, а вплоть до ± несколько сотен. Это позволяет ставить квантовомеханические эксперименты с невиданной ранее свободой действий, резко повышает информационную емкость единичных фотонов, расширяет возможности квантовой криптографии. Наконец, закрученный свет используется как новый метод воздействия на отдельные атомы, на бозе-эйнштейновский конденсат, как новый инструмент исследования в микроскопии, в микромеханике, в оптоэлектронных микроустройствах и даже в астрофизике. Многочисленные примеры можно найти в вышедшей два года назад книге (J. P. Torres, R. Torner, 2011. Twisted Photons).

Как поднять энергию?

Это всё замечательно, но до сих пор возможности экспериментаторов не уходили дальше оптического диапазона (энергия фотонов порядка 1 электронвольта, эВ). А ведь для целого ряда задач очень хочется получить закрученные фотоны намного большей энергии. Скажем, если бы был доступен закрученный рентген (энергии фотонов в сотни эВ и кэВ), то новыми красками заиграл бы рентгеноструктурный анализ вещества и в особенности сложных (в частности, биологически важных) молекул с винтовой закруткой. В атомной физике появился бы способ возбуждать электронные переходы с резким изменением орбитального углового момента — то, что сегодня делается с большим трудом. Если же удастся получить закрученные фотоны с энергиями порядка МэВ и выше, то откроется новый способ возбуждать вращательные состояния ядер, а может быть, даже и элементарных частиц. В общем, перспективы заманчивые — надо лишь сделать такие фотоны реальностью.

К сожалению, стандартные методики закручивания света тут уже не работают. Дело в том, что обычно закрученные фотоны получают так: сначала порождают обычные световые плоские волны с широким и ровным волновым фронтом, а затем пропускают их сквозь специальные дифракционные устройства или иные «маски», вырезающие из световой волны профиль нужной формы (подробности см. в нашей обзорной статье). Но для энергий в сотни эВ и выше трудно найти источники фотонов с хорошей когерентностью и создать подходящие «оптические маски». Поэтому ученые стали склоняться к мысли, что надо кардинально менять саму методику получения закрученных фотонов большой энергии.

Рис. 2. Схема возникновения синхротронного излучения в ондуляторе. Изображение с сайта photon-science.desy.de

В 2007 году в статье Phys. Rev. Lett. 100, 124801 было высказано предложение генерировать яркий пучок закрученного рентгена с помощью ондулятора. Идея заключается вот в чём. Берем обычный ускоритель электронов до умеренно больших энергий (скажем, несколько ГэВ) и прогоняем электронный пучок через прямой участок, на котором в ряд установлено много магнитов чередующейся полярности (рис. 2). Пролетая сквозь такое поле, электронный сгусток будет вилять из стороны в сторону, и, виляя, он будет излучать синхротронное излучение. Это излучение можно сделать довольно мощным, узконаправленным, монохроматичным и, к тому же, с настраиваемой частотой, которая зависит от энергии электронов. Подробнее о принципе работы и применении ондулятора см. в нашей новости Физики создали настольный рентгеновский микроскоп. На этим принципе, в частности, работает лазер на свободных электронах.

Ондуляторы бывают двух основных типов: плоский и спиральный. В первом электронный сгусток колеблется в одной плоскости (как на рис. 2), во втором его траектория представляет собой спираль. Это влияет на свойства излучения: в плоском оно линейно поляризовано, а в спиральном — циркулярно. Но это еще не всё. По расчетам статьи 2007 года получается, что это будет влиять и на закрученность излученных фотонов: излучение с определенным орбитальным угловым моментом будет возникать именно в спиральном ондуляторе.

Правда, тут есть маленькая тонкость, заметно усложняющее дело. Для многих периодических процессов вызываемый ими эффект, если его разложить по колебаниям с определенной частотой, может содержать не только основную (так называемую фундаментальную) частоту, но и кратные частоты: удвоенную, утроенную и т. д. То же справедливо и для ондуляторного излучения: в основном излучение идет на фундаментальной частоте, но есть также излучение и в кратные частоты, правда оно намного слабее. Как показали расчеты, для закручивания фотонов нужна не фундаментальная, а более высокая частота; этот же вывод был затем подтвержден и в статье arXiv:1109.1603.

Закрученный рентген получен

Предложенная идея оказалась не столь простой для реализации. Дело тут не только в том, что излучение ондулятора на кратных частотах слабое и потому обычно не изучается. Оказывается, доказать наличие орбитального углового момента в неплоской волне не так-то и просто. Если таким закрученным светом посветить на экран, то он оставит след в виде аккуратного симметричного колечка. Но такие же колечки яркости можно создать и без закрутки (читатели «Элементов» уже встречались с таким примером в задаче Скорость радиально-поляризованного света). Поэтому для доказательства, что полученные фотоны действительно закручены, желательно использовать какой-то более четкий способ.

Такой способ был придуман и реализован в вышедшей на днях статье Phys. Rev. Lett. 111, 034801 (2013). Благодаря ему физики смогли воочию убедиться, что полученные ими рентгеновские фотоны с энергией 99 эВ действительно несут орбитальный угловой момент.

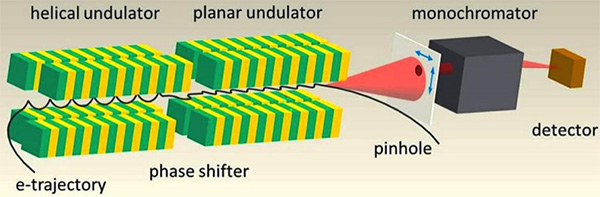
Рис. 3. Схема эксперимента по наблюдению рентгеновского ондуляторного излучения с орбитальным угловым моментом. Изображение из обсуждаемой статьи в Phys. Rev. Lett.

На рис. 3 приведена схема эксперимента, выполненного на немецком электронном накопительном кольце BESSY II. Физики установили на нем особый, двойной ондулятор. Первая половина его заставляла электронный сгусток двигаться по спирали, а затем переводила траекторию в плоскость. Излучение шло на обоих участках, и оно, разумеется, было одинаковой частоты и накладывалось друг на друга. В результате то, что попадало на экран, представляло собой не чистый закрученный рентген, а интерференцию закрученного и незакрученного света, который затем регистрировался специальным монохроматором и детектором.

И вот такая интерференция, как оказалось, приводит к сложному узору, который четко показывает наличие и направление закрученности излучения, порождаемого на первом этапе. На рис. 4 слева показано то, как выглядело распределение интенсивности в реальности, а справа — результаты численного моделирования. Отлично видна спиральная структура излучения, которая хорошо совпадает с результатами моделирования. При изменении направления спиральной траектории в первой половине ондулятора менялось и направление спирали в этом распределении. Подчеркнем, что этот результат относится к излучению на удвоенной частоте; на основной частоте никакой закрутки не было. Ее также не было, разумеется, и при отключении любой из половин ондулятора.

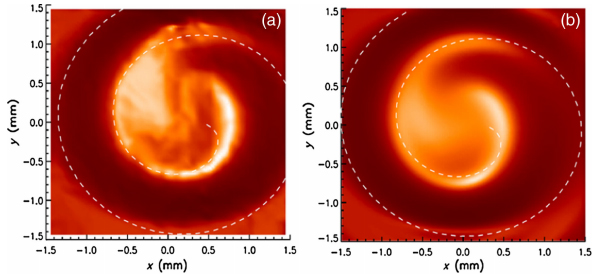
Рис. 4. Экспериментально измеренное (слева) и полученное моделированием (справа) распределение интенсивности излучения в двойном ондуляторе. Изображение из обсуждаемой статьи в Phys. Rev. Lett.

Таким образом, предложенный 6 лет назад метод получения закрученного рентгена был успешно реализован, и физика закрученного света шагнула по шкале электромагнитных волн сразу на два порядка вверх. При желании эксперименты с закрученным рентгеном можно ставить уже сейчас. А параллельно с этим можно попытаться поднять энергию фотонов еще выше: для этого достаточно установить такой же двойной ондулятор в накопительное кольцо с большей энергией электронов. Поскольку в современных электронных коллайдерах уже достижимы энергии порядка 100 ГэВ, а энергия излученных фотонов в ондуляторе квадратично растет с энергией электронов, то и МэВные закрученные фотоны уже кажутся вполне достижимыми.

Источник: J. Bahrdt et al. First Observation of Photons Carrying Orbital Angular Momentum in Undulator Radiation // Phys. Rev. Lett. 111, 034801 (2013).

Игорь Иванов