Арифметика для купцов

Наталья Рожковская
«Квантик» №10, 2016

Во времена эпохи Возрождения развитие торговых связей между европейскими городами привело к новым видам коммерческих отношений.

Умение торговаться, обращаться с валютой разных стран, составлять смету, оформлять кредиты, вести сложную бухгалтерию стало необходимым. Появились специальные школы, где сыновья купцов могли обучиться арифметике. Для этих школ были написаны учебники по математике. Как правило, в этих учебниках разбирались примеры практических подсчётов, предлагалась справочная информация о курсах валют, а также советы о том, как вести учёт продаж.

Например, в знаменитой немецкой книге «Быстрый и приятный счёт для всех торговцев», изданной Иоганном Видманом в 1489-м году, можно встретить такую задачу:

Один человек пришёл к меняле в Вене с 30-ю монетами в нюрнбергской валюте: «Пожалуйста, поменяйте мои 30 монет и дайте мне столько венских монет за них, сколько они стоят». Меняла не знал, сколько венских монет он должен дать человеку. Тогда он пошёл в денежную контору, и там ему дали совет: 7 венских монет стоят 9 монет из Линца, 8 монет из Линца стоят 11 монет из Пассау, 12 монет из Пассау стоят 13 монет из Фильсхофена, 15 монет из Фильсхофена стоят 10 монет из Регенсбурга, 8 монет из Регенсбурга стоят 18 монет из Ноймаркта, а 5 монет из Ноймаркта стоят 4 нюрнбергские монеты. Сколько венских монет стоят 30 нюрнбергских монет?

Однако, несмотря на то, что в Европе в XIV веке уже были широко распространены арабские цифры, единых обозначений для многих стандартных математических операций по-прежнему не существовало, а решения задач записывались не так, как мы привыкли записывать их сегодня в наших школах. Вот несколько примеров из итальянской «Книги Счёта», составленной Джироламо и Джиованни Тальенте примерно в 1520-м году. Сможете ли вы сами догадаться, что представлено на этих диаграммах (они приведены внизу страницы)?

Вы, наверное, сразу догадались, что, например, на первом рисунке число 67048164, написанное внизу, — это произведение чисел 9876 и 6789. Действительно, диаграммы объясняют умножение многозначных чисел. Но что означают остальные числа? Оказывается, это промежуточные результаты. В школе нас научили умножать многозначные числа столбиком. Но есть и другие способы найти произведение двух чисел, и один из них — это умножение решёткой. И сегодня в некоторых школах в других странах этому методу обучают наравне с привычным нам методом умножения столбиком.

Вот как работает этот способ. Допустим, мы хотим умножить 876 на 45. Нарисуем таблицу размером 3 на 2 клетки — по количеству цифр в множителях. Напишем над столбцами цифры первого множителя, числа 876, а рядом со строками — цифры второго множителя, числа 45. Каждую клетку разделим диагональю на две части. Заполним каждую клетку таблицы результатом умножения однозначных чисел соответствующих цифрам, поставив число десятков над диагональю, а число единиц под диагональю клетки. Получим вот такой результат:

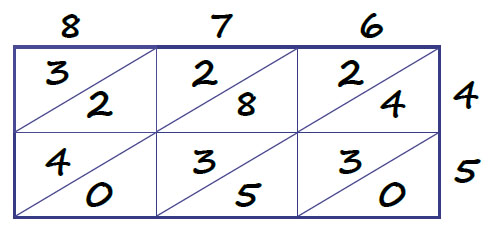
Далее, начиная с нижней правой клетки, сложим числа вдоль косых полос, которые мы отметили чередующимся цветом на следующей диаграмме. Как и в обычном умножении столбиком, под каждой полосой запишем число единиц суммы, а число десятков перенесём в следующую полосу.

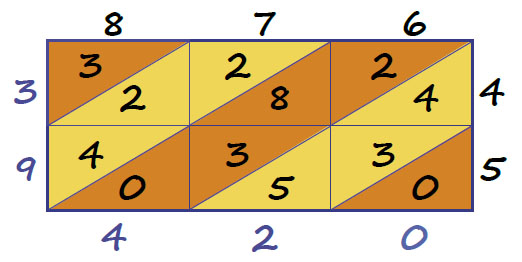
Диаграмма дала нам результат умножения: 876 · 45 = 39420.

Применим теперь метод умножения решёткой к числам 9876 и 6789 из «Книги Счёта». Но выделим в таблице косые полосы в другом направлении, отличном от стандартного метода. Посмотрите, что получилось в таблице в выделенных цветом диагоналях!

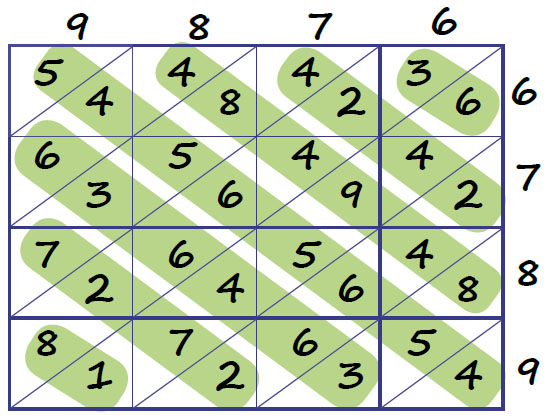
Итак, диаграмма из старинной книги объясняет алгоритм умножения, похожий на метод умножения решёткой, и «в переводе» на современный язык арифметики представляет следующее вычисление:

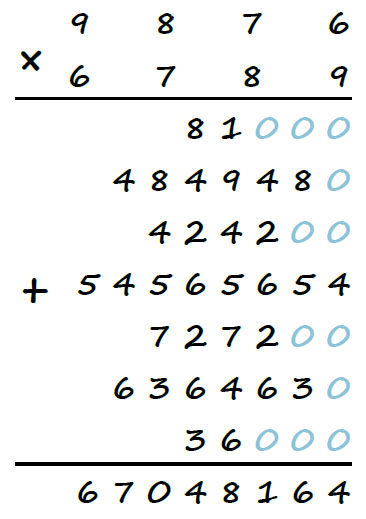
Надеемся, что вы разобрались в этом несложном методе умножения и теперь легко найдёте несколько ошибок в старинном итальянском справочнике.

Художник Мария Усеинова