Что же доказал Григорий Перельман?

Сергей Дужин,
доктор физ.-мат. наук, старший научный сотрудник Санкт-Петербургского отделения Математического института РАН
«Троицкий вариант» №10(104), 22 мая 2012 года

Сергей Дужин. Фото Н. Четвериковой

Последним великим достижением чистой математики называют доказательство петербуржцем Григорием Перельманом в 2002–2003 годах гипотезы Пуанкаре, высказанной в 1904 году и гласящей: «всякое связное, односвязное, компактное трехмерное многообразие без края гомеоморфно сфере S³».

В этой фразе имеется несколько терминов, которые я постараюсь объяснить так, чтобы их общий смысл стал понятен нематематикам (я предполагаю, что читатель закончил среднюю школу и кое-что из школьной математики еще помнит).

Начнем с понятия гомеоморфизма, центрального в топологии. Вообще, топологию часто определяют как «резиновую геометрию», т. е. как науку о свойствах геометрических образов, которые не меняются при плавных деформациях без разрывов и склеек, а точнее, при возможности установить между двумя объектами взаимно-однозначное и взаимно-непрерывное соответствие.

Главную идею проще всего объяснить на классическом примере кружки и бублика. Первую можно превратить во второй непрерывной деформацией.

Эти рисунки наглядно показывают, что кружка гомеоморфна бублику, причем этот факт верен как для их поверхностей (двумерных многообразий, называемых тором), так и для заполненных тел (трехмерных многообразий с краем).

Приведем толкование остальных терминов, фигурирующих в формулировке гипотезы.

1. Трехмерное многообразие без края. Это такой геометрический объект, у которого каждая точка имеет окрестность в виде трехмерного шара. Примерами 3-многообразий может служить, во-первых, всё трехмерное пространство, обозначаемое R³ , а также любые открытые множества точек в R³ , к примеру внутренность полнотория (бублика). Если рассмотреть замкнутое полноторие, т. е. добавить и его граничные точки (поверхность тора), то мы получим уже многообразие с краем — у краевых точек нет окрестностей в виде шарика, но лишь в виде половинки шарика.
2. Связное. Понятие связности здесь самое простое. Многообразие связно, если оно состоит из одного куска, или, что то же самое, любые две его точки можно соединить непрерывной линией, не выходящей за его пределы.
3. Односвязное. Понятие односвязности сложнее. Оно означает, что любую непрерывную замкнутую кривую, расположенную целиком в пределах данного многообразия, можно плавно стянуть в точку, не покидая этого многообразия. Например, обычная двумерная сфера в R³ односвязна (кольцевую резинку, как угодно приложенную к поверхности яблока, можно плавной деформацией стянуть в одну точку, не отрывая резинки от яблока). С другой стороны, окружность и тор неодносвязны.
4. Компактное. Многообразие компактно, если любой его гомеоморфный образ имеет ограниченные размеры. Например, открытый интервал на прямой (все точки отрезка, кроме его концов) некомпактен, так как его можно непрерывно растянуть до бесконечной прямой. А вот замкнутый отрезок (с концами) является компактным многообразием с краем: при любой непрерывной деформации концы переходят в какие-то определенные точки, и весь отрезок обязан переходить в ограниченную кривую, соединяющую эти точки.

Размерность многообразия — это число степеней свободы у точки, которая на нем «живет». У каждой точки есть окрестность в виде диска соответствующей размерности, т. е. интервала прямой в одномерном случае, круга на плоскости в двумерном, шара в трехмерном и т. д. Одномерных связных многообразий без края с точки зрения топологии всего два: это прямая и окружность. Из них только окружность компактна.

Примером пространства, не являющегося многообразием, может служить, например, пара пересекающихся линий — ведь у точки пересечения двух линий любая окрестность имеет форму креста, у нее нет окрестности, которая была бы сама по себе просто интервалом (а у всех других точек такие окрестности есть). Математики в таких случаях говорят, что мы имеем дело с особым многообразием, у которого есть одна особая точка.

Двумерные компактные многообразия хорошо известны. Если рассматривать только ориентируемые¹ многообразия без края, то они с топологической точки зрения составляют простой, хотя и бесконечный, список: и так далее. Каждое такое многообразие получается из сферы приклеиванием нескольких ручек, число которых называется родом поверхности.

На рисунке изображены поверхности рода 0, 1, 2 и 3. Чем выделяется сфера из всех поверхностей этого списка? Оказывается, односвязностью: на сфере любую замкнутую кривую можно стянуть в точку, а на любой другой поверхности всегда можно указать кривую, которую стянуть в точку по поверхности невозможно.

Любопытно, что и трехмерные компактные многообразия без края можно в некотором смысле классифицировать, т. е. выстроить в некоторый список, хотя не такой прямолинейный, как в двумерном случае, а имеющий довольно сложную структуру. Тем не менее, трехмерная сфера S³ выделяется в этом списке точно так же, как двумерная сфера в списке, приведенном выше. Тот факт, что любая кривая на S³ стягивается в точку, доказывается столь же просто, как и в двумерном случае. А вот обратное утверждение, а именно, что это свойство уникально именно для сферы, т. е. что на любом другом трехмерном многообразии есть нестягиваемые кривые, очень трудное и в точности составляет содержание гипотезы Пуанкаре, о которой мы ведем речь.

Важно понимать, что многообразие может жить само по себе, о нем можно мыслить как о независимом объекте, никуда не вложенном. (Представьте себе жизнь двумерных существ на поверхности обычной сферы, не подозревающих о существовании третьего измерения.) К счастью, все двумерные поверхности из приведенного выше списка можно вложить в обычное пространство R³, что облегчает их визуализацию. Для трехмерной сферы S³ (и вообще для любого компактного трехмерного многообразия без края) это уже не так, поэтому необходимы некоторые усилия для того, чтобы понять ее строение.

По-видимому, простейший способ объяснить топологическое устройство трехмерной сферы S³ — это при помощи одноточечной компактификации. А именно, трехмерная сфера S³ представляет собой одноточечную компактификацию обычного трехмерного (неограниченного) пространства R³.

Поясним эту конструкцию сначала на простых примерах. Возьмем обычную бесконечную прямую (одномерный аналог пространства) и добавим к ней одну «бесконечно удаленную» точку, считая, что при движении по прямой вправо или влево мы в конце концов попадаем в эту точку. С топологической точки зрения нет разницы между бесконечной прямой и ограниченным открытым отрезком (без концевых точек). Такой отрезок можно непрерывно изогнуть в виде дуги, свести поближе концы и вклеить в место стыка недостающую точку. Мы получим, очевидно, окружность — одномерный аналог сферы.

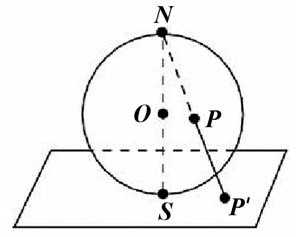
Подобным же образом, если я возьму бесконечную плоскость и добавлю одну точку на бесконечности, к которой стремятся все прямые исходной плоскости, проходимые в любом направлении, то мы получим двумерную (обычную) сферу S² . Эту процедуру можно наблюдать при помощи стереографической проекции, которая каждой точке P сферы, за исключением северного полюса N, ставит в соответствие некоторую точку плоскости P'.

Таким образом, сфера без одной точки — это топологически все равно, что плоскость, а добавление точки превращает плоскость в сферу.

В принципе, точно такая же конструкция применима и к трехмерной сфере и трехмерному пространству, только для ее осуществления необходим выход в четвертое измерение, и на чертеже это не так просто изобразить. Поэтому я ограничусь словесным описанием одноточечной компактификации пространства R³.

Представьте себе, что к нашему физическому пространству (которое мы, вслед за Ньютоном, считаем неограниченным евклидовым пространством с тремя координатами x, y, z) добавлена одна точка «на бесконечности» таким образом, что при движении по прямой в любом направлении вы в нее попадаете (т. е. каждая пространственная прямая замыкается в окружность). Тогда мы получим компактное трехмерное многообразие, которое и есть по определению сфера S³.

Легко понять, что сфера S³ односвязна. В самом деле, любую замкнутую кривую на этой сфере можно немного сдвинуть, чтобы она не проходила через добавленную точку. Тогда мы получим кривую в обычном пространстве R³, которая легко стягивается в точку посредством гомотетий, т. е. непрерывного сжатия по всем трем направлениям.

Для понимания, как устроено многообразие S³, весьма поучительно рассмотреть его разбиение на два полнотория. Если из пространства R³ выбросить полноторие, то останется нечто не очень понятное. А если пространство компактифицировать в сферу, то это дополнение превращается тоже в полноторие. То есть сфера S³ разбивается на два полнотория, имеющих общую границу — тор.

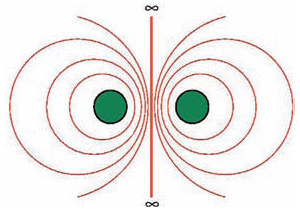
Вот как это можно понять. Вложим тор в R³ как обычно, в виде круглого бублика, и проведем вертикальную прямую — ось вращения этого бублика. Через ось проведем произвольную плоскость, она пересечет наше полноторие по двум кругам, показанным на рисунке зеленым цветом, а дополнительная часть плоскости разбивается на непрерывное семейство красных окружностей. К их числу относится и центральная ось, выделенная более жирно, потому что в сфере S³ прямая замыкается в окружность. Трехмерная картина получается из этой двумерной вращением вокруг оси. Полный набор повернутых окружностей заполнит при этом трехмерное тело, гомеоморфное полноторию, только выглядящее необычно.

В самом деле, центральная ось будет в нем осевой окружностью, а остальные будут играть роль параллелей — окружностей, составляющих обычное полноторие.

Чтобы было с чем сравнивать 3-сферу, я приведу еще один пример компактного 3-многообразия, а именно трехмерный тор. Трехмерный тор можно построить следующим образом. Возьмем в качестве исходного материала обычный трехмерный куб:

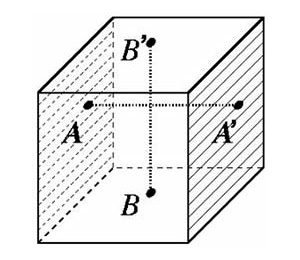
В нем имеется три пары граней: левая и правая, верхняя и нижняя, передняя и задняя. В каждой паре параллельных граней отождествим попарно точки, получающиеся друг из друга переносом вдоль ребра куба. То есть будем считать (чисто абстрактно, без применения физических деформаций), что, например, A и A' — это одна и та же точка, а B и B' — тоже одна точка, но отличная от точки A. Все внутренние точки куба будем рассматривать как обычно. Сам по себе куб — это многообразие с краем, но после проделанных склеек край замыкается сам на себя и исчезает. В самом деле, окрестностями точек A и A' в кубе (они лежат на левой и правой заштрихованных гранях) служат половинки шаров, которые после склейки граней сливаются в целый шарик, служащий окрестностью соответствующей точки трехмерного тора.

Чтобы ощутить устройство 3-тора исходя из обыденных представлений о физическом пространстве, нужно выбрать три взаимно перпендикулярных направления: вперед, влево и вверх — и мысленно считать, как в фантастических рассказах, что при движении в любом из этих направлений достаточно долгое, но конечное время, мы вернемся в исходную точку, но с противоположного направления. Это тоже «компактификация пространства», но не одноточечная, использованная раньше для построения сферы, а более сложная.

На трехмерном торе есть нестягиваемые пути; например, таковым является отрезок AA' на рисунке (на торе он изображает замкнутый путь). Его нельзя стянуть, потому что при любой непрерывной деформации точки A и A' обязаны двигаться по своим граням, оставаясь строго друг напротив друга (иначе кривая разомкнется).

Итак, мы видим, что бывают односвязные и неодносвязные компактные 3-многообразия. Перельман доказал, что односвязное многообразие ровно одно.

Исходной идеей доказательства является использование так называемого «потока Риччи»: мы берем односвязное компактное 3-многообразие, наделяем его произвольной геометрией (т. е. вводим некоторую метрику с расстояниями и углами), а затем рассматриваем его эволюцию вдоль потока Риччи. Ричард Гамильтон, который высказал эту идею в 1981 году, надеялся, что при такой эволюции наше многообразие превратится в сферу. Оказалось, что это неверно, — в трехмерном случае поток Риччи способен портить многообразие, т. е. делать из него немногообразие (нечто с особыми точками, как в приведенном выше примере пересекающихся прямых). Перельману путем преодоления неимоверных технических трудностей, с использованием тяжелого аппарата уравнений с частными производными, удалось внести поправки в поток Риччи вблизи особых точек таким образом, что при эволюции топология многообразия не меняется, особых точек не возникает, а в конце концов, оно превращается в круглую сферу. Но нужно объяснить, наконец, что же такое этот поток Риччи. Потоки, использованные Гамильтоном и Перельманом, относятся к изменению внутренней метрики на абстрактном многообразии, и это объяснить довольно трудно, поэтому я ограничусь описанием «внешнего» потока Риччи на одномерных многообразиях, вложенных в плоскость.

Представим себе гладкую замкнутую кривую на евклидовой плоскости, выберем на ней направление и рассмотрим в каждой точке касательный вектор единичной длины. Тогда при обходе кривой в выбранном направлении этот вектор будет поворачиваться с какой-то угловой скоростью, которая называется кривизной. В тех местах, где кривая изогнута круче, кривизна (по абсолютной величине) будет больше, а там, где она более плавная, кривизна будет меньше.

Кривизну будем считать положительной, если вектор скорости поворачивает в сторону внутренней части плоскости, разбитой нашей кривой на две части, и отрицательной, если он поворачивает вовне. Это соглашение не зависит от направления обхода кривой. В точках перегиба, где вращение меняет направление, кривизна будет равна 0. Например, окружность радиуса 1 имеет постоянную положительную кривизну, равную 1 (если считать ее в радианах).

Теперь забудем про касательные векторы и к каждой точке кривой прикрепим, наоборот, перпендикулярный ей вектор, по длине равный кривизне в данной точке и направленный вовнутрь, если кривизна положительна, и вовне, если отрицательна, а затем заставим каждую точку двигаться в направлении соответствующего вектора со скоростью, пропорциональной его длине. Вот пример:

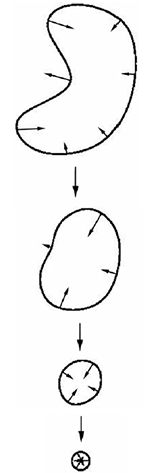
Оказывается, что любая замкнутая кривая на плоскости ведет себя при такой эволюции подобным же образом, т. е. превращается, в конце концов, в окружность. Это и есть доказательство одномерного аналога гипотезы Пуанкаре при помощи потока Риччи (впрочем, само утверждение в данном случае и так очевидно, просто способ доказательства иллюстрирует, что происходит в размерности 3).

Заметим в заключение, что рассуждение Перельмана доказывает не только гипотезу Пуанкаре, но и гораздо более общую гипотезу геометризации Тёрстона, которая в известном смысле описывает устройство всех вообще компактных трехмерных многообразий. Но этот предмет лежит уже за рамками настоящей элементарной статьи.

¹ За неимением места, я не буду говорить о неориентируемых многообразиях, примером которых может служить известная бутылка Клейна — поверхность, которую нельзя вложить в пространство без самопересечений.