Настоящая температура не может быть отрицательной
В последние годы стали всё чаще встречаться научные сообщения об экспериментальной реализации систем с отрицательной абсолютной температурой. Хотя каждый раз ученым было понятно, о чем именно идет речь, оставалось непонятным, насколько широко этот термин разрешено использовать в термодинамике — ведь известно, что строгая термодинамика отрицательных температур не приемлет. Методическая статья, вышедшая на днях в журнале Nature Physics, расставляет вещи по своим местам.
Суть работы
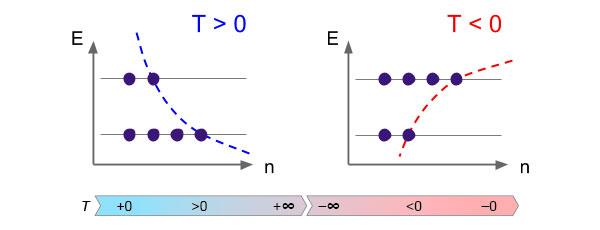
В школе проходят, что абсолютная температура — та самая, которая отсчитывается от абсолютного нуля и измеряется в кельвинах, а не в градусах Цельсия, — обязана быть положительной. Однако в современной физике, а вслед за ней и в популярных материалах, сплошь и рядом встречаются статьи про экзотические системы, характеризующиеся отрицательной абсолютной температурой. Стандартный пример — коллектив атомов, каждый из которых может находиться всего в двух энергетических состояниях. Если сделать так, чтобы количество атомов в верхнем энергетическом состоянии было больше, чем в нижнем, то как бы получается отрицательная температура (рис. 1). При этом обязательно подчеркивается, что отрицательные температуры — это не очень холодные температуры, ниже абсолютного нуля, а наоборот — экстремально горячие, горячее любой положительной температуры.
Такие ситуации можно даже получать экспериментально; впервые это было сделано еще в 1951 году. Но поскольку сами эти ситуации были необычны, до поры до времени отношение ученых к этой теме было умеренно спокойное: это некое любопытное эффективное описание необычных ситуаций, но к нормальным термодинамическим системам, в которых тепло связано с пространственным движением, оно не относится.
Ситуация стала меняться в последние годы. Несколько лет назад были предсказаны системы с отрицательной температурой, связанной с движением частиц (см. новость Предсказан газ с отрицательной кинетической температурой, «Элементы», 29.08.2005), а буквально в этом году появилась статья с экспериментальной реализацией подобной ситуации (подробности см., например, в заметке В эксперименте удалось получить устойчивую температуру ниже абсолютного нуля, «Компьюлента», 09.01.2013). Более того, ученые не просто получили такие системы, но и начали всерьез рассуждать о настоящей термодинамике с отрицательными температурами (тепловые машины с КПД выше 100%) и даже о ее возможной роли в загадке темной энергии. Таким образом, по крайней мере для части физиков, отрицательные температуры перестали казаться математическим трюком, а стали чем-то вполне реальным.
На днях в журнале Nature Physics вышла статья, которая поставила ребром вопрос о физичности термина «отрицательная температура» в настоящей термодинамике. Статья эта была, в сущности, методическая, а не исследовательская, однако в ней четко сформулированы несколько важных вещей:
- Понятие температуры можно определять разными способами, и все разговоры об отрицательной температуре относятся только к одному конкретному определению. Для подавляющего большинства систем эти разные температуры практически неотличимы, поэтому неважно, каким определением пользоваться.
- Для необычных систем эти температуры могут различаться, и причем — различаться кардинально. Так, обычное определение температуры может давать отрицательный результат, а другое определение — всегда положительный.
- В рамках строгой термодинамики требуется, чтобы термодинамическая температура была всегда положительна. Поэтому то определение, которое приводит к отрицательным значениям, — это ненастоящая температура. Ею можно пользоваться, никто этого не запрещает, но ее нельзя подставлять в настоящие термодинамические формулы или придавать ей излишне физическое значение.
Иными словами, эта статья призывает умерить воодушевление, вызванное недавними экспериментальными достижениями.
Для неискушенного читателя это всё может показаться странным: как так — несколько температур? какая такая строгая термодинамика? Поэтому мы приводим ниже чуть более подробное, но и более техническое описание ситуации.
Подробное пояснение
Мы привыкли, что тепло — а значит, и температура как численная мера тепла — является чем-то таким осязаемым, понятным. Казалось бы, если уж в физике и есть проблемы с температурой, то они могут касаться измерения температуры в каких-то сложных случаях, но никак не ее определения. Однако новая статья говорит, что температур две и одна из них в каком-то смысле «неправильная». Как это понимать?
Для объяснения ситуации надо отступить немножко назад, отойти от прикладных аспектов термодинамики и заглянуть в ее суть, в ее аккуратную формулировку. Термодинамика — это наука о тепловых процессах, всё верно, но только понятие «температура» в ней появляется вовсе не на первом этапе. Термодинамика начинается с математики, с введения неких абстрактных величин и установления их математических свойств. Считается, что у системы есть объем, количество вещества, некая внутренняя энергия, — это всё пока еще механические характеристики, — а также новая характеристика, называемая энтропией. Именно с введения энтропии начинается термодинамика, однако что такое энтропия — на этом этапе не обсуждается. Энтропия тоже обязана обладать определенными математическими свойствами, которые можно аккуратно сформулировать как настоящие аксиомы. Желающим вкратце познакомиться с этой настоящей математической стороной вопроса можно порекомендовать статью A Guide to Entropy and the Second Law of Thermodynamics, опубликованную в математическом (!) журнале. В принципе, это всё было более-менее известно еще век назад, но в таком аккуратном математическом виде это было сформулировано лишь в последние десятилетия.
Итак, именно энтропия является той величиной, из которой следует вся привычная термодинамика. В частности, температура (а точнее, 1/T) определяется как скорость изменения энтропии с ростом внутренней энергии. И если следовать всем аксиомам термодинамики, то эта настоящая термодинамическая температура обязана быть положительной.
Всё бы хорошо, но только в этом строгом математическом построении термодинамики нет ни слова о том, чему равняется энтропия, как именно она зависит от внутренней энергии. Эта математическая формулировка является неким «универсальным вместилищем» для разнообразных реальных ситуаций, но в ней не говорится, как именно ее надо применять к конкретным системам. Возникает задача о том, как вписать реальные системы, состоящие из большого числа атомов и молекул, в термодинамику.
Этим занимается уже другая наука — статистическая физика. Это тоже очень серьезная и уважаемая дисциплина, опирающаяся на квантовую механику систем из нескольких частиц и на аккуратную математику. В частности, вы в ней можете сосчитать не только энергию коллектива из нескольких частиц, находящихся в заданной конфигурации, но и, наоборот, найти число состояний — сколько может быть разных конфигураций с заданной полной энергией. Это всё тоже хорошо, но энтропии в этой картине пока нет.
Остался один шаг — переход от статистической физики к термодинамике. Это тоже теоретический, а не экспериментальный шаг: нам надо постановить, как энтропию вычислить из числа состояний. Конечно, тут налагается требование, что вычисленная таким образом энтропия должна обладать правильными свойствами — по крайней мере, для всех жизненных ситуаций. И вот тут появляется неоднозначность: оказывается, сделать это можно по-разному.
Еще в эпоху построения статистической физики было предложено два слегка различающихся способа: энтропия по Больцману, SB, и энтропия по Гиббсу, SG. Энтропия по Больцману характеризует концентрацию энергетических состояний вблизи данной энергии, энтропия по Гиббсу — полное число состояний с энергией меньше данной энергии; см. пояснения на рис. 2. Соответственно, и температуры в этих двух картинах были разные: температура по Больцману, TB, и температура по Гиббсу, TG. Получается, можно построить две разные термодинамики для одной и той же системы.

Рис. 2. Два определения энтропии — по Больцману и по Гиббсу — могут давать сильно разные результаты для соответствующих температур. Рассмотрим систему, у которой плотность энергетических уровней уменьшается с ростом энергии. Энтропия по Больцману (SB) — это логарифм от количества уровней внутри небольшого интервала ΔE. Энтропия по Гиббсу (SG) — это логарифм от полного числа уровней ниже данной энергии. Для изображенной системы SB уменьшается с ростом энергии, а SG — растет. Поэтому температура по Больцману получается отрицательной, а по Гиббсу — положительной
Для всех реальных ситуаций эти две термодинамики настолько близки, что их различить просто нереально. Поэтому в большинстве учебников по статистической физике и термодинамике этого различия вообще не проводится, а в качестве опоры выбирается термодинамика по Больцману. Но если соответствующую температуру TB использовать в некоторых экзотических ситуациях, то она действительно может принимать отрицательное значение. Самые простые примеры, приведенные в статье, — это стандартная ситуация (много частиц на двух энергетических уровнях) и одна-единственная квантовая частица в одномерном прямоугольном потенциале. В обоих случая непонятно, насколько вообще оправдано применение термодинамических понятий к таким системам.
Зато определение температуры по Гиббсу, TG, остается осмысленным всегда, даже в тех экзотических ситуациях, где применимость термодинамики спорна. При повышении средней энергии температура плавно растет, но никогда не становится бесконечной и не прыгает потом в отрицательные значения. Поэтому если уж мы и беремся строить термодинамику для таких систем, то надо идентифицировать настоящую температуру именно с TG, а не c TB; построенная таким образом термодинамика будет удовлетворять всем аксиомам теории.
Авторы статьи подводят итог, который очень типичен для многих спорных ситуаций в физике: можно использовать любое определение, но всегда надо помнить про сделанные при этом предположения и возникающие ограничения применимости. Стандартное определение температуры грешит тем, что оно в экзотических ситуациях перестает отвечать математическим требованиям термодинамической теории, а также не является адекватной мерой тепла. Поэтому авторы призывают физиков не придавать слишком большого значения отрицательным температурам, а в качестве более надежной опоры для сложных ситуаций они предлагают использовать определение температуры по Гиббсу. Не возбраняется также пытаться расширить границы термодинамики, придумывая некоторые обобщения этой теории, — но надо всегда помнить, что это уже будет не настоящая термодинамика и что в этих ситуациях не все настоящие термодинамические результаты работают.
Источник: J. Dunkel and S. Hilbert, Consistent thermostatistics forbids negative absolute temperatures // Nature Physics. Published online 08 December 2013. Doi:10.1038/nphys2815.
См. также:
1) E. H. Lieb, J. Yngvason. The Physics and Mathematics of the Second Law of Thermodynamics // Physics Reports. 1999. V. 310. P. 1. Статья доступна как е-принт cond-mat/9708200.
2) E. H. Lieb, J. Yngvason. A Guide to Entropy and the Second Law of Thermodynamics // AMS Notices. 1998. V. 45, P. 571.
3) Д. Поулз. Отрицательные абсолютные температуры и температуры во вращающихся системах координат // УФН. 1964. Т. 84. Стр. 693.
-
Как интересно. Да, нас учили определению температуры по Больцману.
Теперь эта температура стала ненастоящей. Хорошо бы сий тезис не только постулировать, но и аргументировать.-
Как уже сказали, вся заметка, в общем-то, про это. T_B — не единственное определение температуры, удовлетворяющее всем требованиям в термодинамическом пределе, если и другие, которые — в этом же пределе — с ней совпадают. В универе учат обычно только этому.
Но поскольку люди хотят использовать термодинамику _не только_ в термодинамическом пределе, то там начинаются различия. Если хотите, можете вообще лишить людей права говорить о ТД вне этого предела, но если позволяете, то вам придется решить, какое определение лучше. В работе показывается, что T_G ничем не хуже, а в некоторых ситуациях и лучше, чем T_B. Вполне естественно желание принять ее как более надежное определение температуры.-
В статье написано иначе - "это ненастоящая температура".
Из того что определение не единственное нельзя сделать вывод о том, что больцмановское определение ненастоящее, как и то что другое определение настоящее. Других аргументов в статье нет.
Поскольку статья популярная, разумеется в ней не нужны доказательства. А вот аргументация нужна. Боюсь только что аргументации "ненастоящести" не найдется. -
-
«Да шо вы так переживаете!» :)
Никто не говорит, что эта наука неправильная. Никто не говорит, что формулы ошибочны. Никто не говорит, что больцмановская температура приводит к ошибочным _вычислительным_ предсказаниям.
Речь лишь про то, что не надо в разговоре про отрицательные температуры высасывать из пальца больше смысла, чем там есть.
Если уж вы так придираетесь к слову «неправильная», то придется потратить 15 минут и пояснить. Слово «неправильная» используется в этой заметке не в смысле «вычислительно ошибочная», а в смысле «не самая лучшая среди альтернатив». Польза от этого слова в таком понимании в том, что оно передает корректное и вместе с тем понятное для широкой публики общее отношение автора статьи в Nature Physics к этой проблеме. Надо как бы не забывать, что эта новость написана не только для тех, кто изучал статфизику в университете, но и для всех интересующихся физикой, в том числе без университетского образования. Поэтому новость должна содержать часть, которую сможет ухватить человек без естественнонаучного образования, а также часть, которая должна удовлетворить интерес людей уже немножко «в теме». В типичной новости я стараюсь вначале дать самую общую и грубую картину, а потом последовательными приближениями ее улучшать. Разумеется, я не пускаюсь в формулы или излишнюю терминологию; я останавливаюсь тогда, когда, как мне кажется, я передал основную идею не только широкой публике, но и ученым. Эта общая идея уже должна помочь физику увидеть вопрос целиком, а разнообразные неточности и недосказанности, которые возникают в популярной новости, он уже сможет быстро восстановить для себя сам.
Разумеется, я мог бы написать и отдельный текст, терминологически корректный и с формулами, который был бы ориентирован как минимум на студентов-физиков. Но цель заметок на этом сайте совсем другая! Поэтому если что-то режет вам глаз, вы поизучайте сами этот вопрос дальше, благо все ссылки у меня поставлены. Я в этих новостях рассчитываю, что уж знающий-то человек сможет помочь себе сам после общего введения :)-
Игорь!Как Вам еще не надоело терпеть этих **даков?Заблокируйте их и всего делов,зачем терпеть каждый раз набеги идиотов и шизофреников?Вы умный,молодой и перспективный ученый,не тратьте свое драгоценное время на идиотов.
PS: Огромное спасибо за Ваш труд,всего Вам наилучшего и еще раз спасибо,за очередную интереснейшую статью! -
А Вам известно, что Альберт Эйнштейн - шизофреник! Это не афишируется, но это так. И чтобы сочинить современную ОТО, ему пришлось выйти на грань сумасшествия! Современные психиатры считают шизофрению болезнью великих людей! К сожалению, всё это оффтопик. Не надо валить всё на шизофреников! Без Эйнштейна было бы скучно в нашем мире!
-
Так же,как и Академик Александров,так же как и Джон Нэш,люди с техническим складом ума склонны к шизофрении.
Но вот в чем собственно дело,Александров,Эйнштейн не были **даками,вроде тех,что здесь иногда пишут.
К Эйнштейну вообще претензий никаких быть не может,их нужно предъявлять тем козлам которые превращают нормальные научные ресурсы в место для пропаганды мракобесия.
-
-
Никуда ему выйти не пришлось, не придумывайте. Элементы ОТО появлялись уже в трудах Римана, Пуанкаре, Лоренца.
-
-
-
Или можно пускать на сайт по спецпропускам.
Спросить ученого здесь не получится. :) Предлагаю всем неученым уйти на более адекватные сайты. Теорию струн изучаемую вполне серьезными учеными уже объявили околофизической темой. Хотя по ней делают доклады, лекции, есть суперструнная теория. Труд огромного количества довольно неглупых специалистов перечеркнули одним движением. Да кому это интересно, учите механику Ньютона и СТО :)
Добавлю, что в последнее время появляется особенно много словосочетаний, искажающих физическую картину. Например: рассматривать голограмму. Ее ведь никто и не рассматривает. Рассматривают голографическое изображение, т.е. изображение, которое формируется при дифракции волны на голограмме и находится вне поверхности голограммы. На мой взгляд, причина появления таких казусов - проникновение жаргона в научные и популярные публикации из-за саморекламы и узкого кругозора пишущих. Про физические термины, их "перевод" на русский и их истолкование, встречающиеся в рекламе различных приборов и устройств для массового потребителя, даже упоминать не хочется. Свою лепту вносят и многочисленные стандарты, утвержденные и изданные в России, являющиеся выполненными не специалистами переводами международных стандартов. Хорошо, что в них есть ссылка на англоязычный первоисточник, написанный понятным языком, добросовестно отредактированный и доступный в сети.
-
Гулять, так гулять.
Как правильно отмечено выше, здесь не только студенты - физики, но судя по всему, есть ученые, которые не утратили бунтарский дух, инженеры, министры и генералы втайне от всех интересующиеся наукой, деды морозы, а также студенты - психиатры, которые по привычке, сразу пустились всем ставить диагнозы. Деду морозу поставили диагноз в раздвоении личности, всех гениев и не очень заподозрили в шизофрении, заболевания других обозвали непонятным термином «**ДАК». Хотя как отмечал Игорь, с научной точки зрения это не совсем соответствует действительности. Как правильно заметила Лайма2001 «На мой взгляд, причина появления таких казусов - проникновение чуждого жаргона в научные и популярные публикации из-за саморекламы и узкого кругозора пишущих. Добавлю, что в последнее время появляется особенно много словосочетаний, искажающих клиническую (физическую-зачеркнуто) картину.» Методическая статья, вышедшая на днях в журнале Nature Physics, расставляет вещи по своим местам. Поэтому, по поводу раздвоения личности у деда мороза и **ДАКОВ, я с Викторией категорически не согласен. А всем здесь присутствующим людям желаю в Новом году быть друг к другу более доброжелательными.
Лайма2001 прошу извинить за цитирование понравившихся мне цитат.
-
Мне кажется, вы смешиваете здесь свое недопонимание статфизики с университетских времен и обсуждаемый в этой статье вопрос. В стандартном выводе энтропии по Больцману для макроскопически больших систем никакого обмана нет. Вы никогда не сможете зафиксировать такую систему в фиксированном микросостоянии — даже если вы заэкранируете ее от воздействия все на свете, у вас все равно не хватит времени жизни вселенной для достаточной локализации энергии. Поэтому вместо чудовищно частого частокола из дельта-функций по энергии у вас неизбежно будет некое размазанное не небольшому интервалу плавное распределение. Вопрос о том, какой выбирать область размытия, совершенно несуществен: вы можете его увеличить или уменьшить в миллион раз, для макроскопического числа частиц это будут пустяки. Вы можете даже выбирать интервал усреднения не постоянный, а тоже растущий с энергией, разницы вы не заметите. Вы можете даже этот интервал экстремально увеличивать с ростом E, так чтоб он покрывал весь доступный диапазон энергий (это и будет энтропия по Гиббсу) — результат все равно существенно не изменится. Грубо говоря, логарифмы от объема N-мерного шара и от площади поверхности этого шара ведут себя как N lnR и (N-1)lnR, и при N порядка числа Авогадро они практически одинаковые. Именно поэтому вам не сильно важно, как именно определять энтропию для макроскопической системы.
Для маленькой системы или для системы с ограниченным сверху спектром отличие возникает. Но там появляется множество других сложных вопросов, например, на основании чего вообще можно говорить про термализацию такой системы, про статистическое равновесие, про введение термодинамических характеристик и т.п. Речь прежде всего идет не о том, какая энтропия или температура правильная, а о том, имеем ли мы право вообще вводить энтропию или температуру. Статья утверждает, что если мы уж вообще готовы делать допущения и вводить термодинамические величины в такой системе, то лучше это делать так, чтобы не влезать в противоречие с формальной термодинамикой и не делать из этих противоречий слишком смелых выводов. Автор показывает, что есть более удобное определение энтропии и температуры, которое этому критерию удовлетворяет.-
Да, все как бы правильно. Но дело-то в том, что я эти аргументы знаю, но не понимаю. Я упоминал Пенроуза, он ровно это и пишет. Я попытаюсь уточнить свое непонимание. Рассмотрим потенциальный ящик с НЕСКОЛЬКИМИ частицами (чтоб их там было не сильно много). Для этой простой системы энергия, равно как и температура, имеют вполне ясный смысл. Если рассматривать систему как классическую и наблюдать ее достаточно долго, то обнаружится равнораспределение энергии по степеням свободы, что и требуется. Если смотреть на нее как на квантовую, то делим полную энергию на число степеней свободы (ну и еще пополам), и тоже получаем температуру. Есть у системы и определенный объем (ящик), и число частиц. Всё это термодинамические параметры и все они хорошо определены. А вот Больцмановской энтропии нет (это потому, что частиц-то мало). Неравноправие какое-то, ведь энтропия - тоже термодинамический параметр не хуже других! Но дело не в том, что энтропия - это какая-то особенная функция состояния, по сравнению с другими. Дело (я так думаю) в том, что с определением Больцмана что-то не то. Но энтропию Гиббса легко определить и для системы нескольких частиц. Поэтому я и думаю, что именно это и есть, в определенном смысле, настоящее определение энтропии, оно обладает точно такой же гибкостью, как температура, объем и число частиц. Чего нельзя сказать об определении Больцмана. Бывает, что и температуру или число частиц нельзя определить, тогда не будет и энтропии Гиббса. Но это уже чисто микроскопическая система.
-
Вы слишком лихо начали всё упрощать.
> Для этой простой системы энергия, равно как и температура, имеют вполне ясный смысл.
Я вот пытаюсь объяснить, что это совершенно не так. Энергия — пожалуйста, это механика, а температура — ни в коей мере не имеют «ясного смысла».
> Если рассматривать систему как классическую и наблюдать ее достаточно долго, то обнаружится равнораспределение энергии по степеням свободы, что и требуется.
Вы эргодическую гипотезу автоматически считаете доказанной для любых систем теоремой? А с интегрируемыми системами вы что будете делать? Там никакой термализации не наступает. Если вы рассмотрите простую одномерную цепочку — одинаковые грузики на одинаковых пружинках — и попробуете сосчитать ее теплопроводность (т.е. с одного конца мы хаотично дергаем, а потом отслеживаем, что происходит по всей цепочке), то у вас ничего не выйдет — в этой системе _нет_ обычной теплопроводности. Там баллистический перенос колебаний, не диффузный. Так что там нет нормально определенной температуры.
> Если смотреть на нее как на квантовую, то делим полную энергию на число степеней свободы (ну и еще пополам), и тоже получаем температуру.
Температура — это не энергия в расчете на одну частицу! Вы какую энергию будете брать-то? «Внутреннюю»? Полную? Кинетическую? Скажите тогда, какова температура у электронов в атоме в основном состоянии? Даже если у вас просто коробка со стенками без потенциалов, то вы возьмите несколько невзаимодействующих бозе частиц, посадите все в основное состояние, у вас же там останется некая энергия. Вы какую будете приписывать температуру?
> Дело (я так думаю) в том, что с определением Больцмана что-то не то.
Нормально с ним всё. В каноническом распределении оно как раз и возникает. Поэтому один из первых пунктов той статьи было утверждение про то, что для систем с отрицательной температурой (например, с инверсной заселенностью) нельзя применять каноническое, а нужно микроканоническое, поскольку система с инверсной заселенностью обязана быть изолированной, она не имеет права находиться в тепловом контакте с окружающей средой, т.к. станет нестабильной.
В общем, не надо всё так тривиализировать. Есть много тонких мест, которые вы пропускаете.-
>Вы слишком лихо начали всё упрощать.
Я не упрощаю, я рассматриваю специально очень простые системы, которые вполне допустимо рассматривать. Я недостаточно точно сформулировал свою мысль. Например, идеальный газ с исчезающе слабым, но ненулевым, взаимодействием между частицами (причем частиц мало). Б.Б. Кадомцев, кажется, вообще рассматривал в качестве термодинамической системы идеальный газ, представленный единственной классической частицей в термостате (это в "Физике и информации"). Термодинамической (точнее даже термостатической) системой является, вообще говоря, не система, в которой много частиц или много степеней свободы, а система, где можно провести эффективное усреднение (хоть по ансамблю, хоть по времени), и получить макроскопические величины. Для усреднения по времени, естественно, нужна эргодичность. Точнее, возможность усреднения является достаточным условием термодинамичности. Например, для единственной частицы в сосуде таким образом вводится давление на стенки. Я вовсе не утверждаю, что все малочастичные системы являются простыми (естественно, это не так), но такие (пусть даже идеализированные) простые системы могут существовать. И вот, например, для почти идеального классического (никаких конденсатов) газа температура (которая вводится просто как мера средней кинетической энергии), давление, объем хорошо определены, а энтропия по Больцману - нет. Но энтропия по Гиббсу все равно определена. Достаточно существования хотя бы одного примера, в котором энтропию Больцмана определить нельзя, а энтропию и Гиббса - можно, чтобы показать, что это совсем разные вещи. Универсальности от примера не требуется. Это как принцип фальсифицируемости: достаточно единственного фальсифицирующего примера, и теория будет опровергнута, независимо о количества подтверждающих примеров. Кстати, вот "практический" пример системы, которая удовлетворяет всем требованиям с высокой точностью: газ, состоящий ровно из пяти атомов: по одному атому гелия, неона, аргона, криптона и ксенона в какой-нибудь ловушке не слишком маленького и не слишком большого размера, при не слишком низкой температуре и не слишком высокой температуре.
-
-
-
Последние новости














Рис. 1. Для описания коллектива атомов, которые могут находиться только на двух энергетических уровнях, тоже можно вводить понятие температуры в согласии с формулой: число частиц n ∼ exp(−E/kT). Если на верхнем уровне оказывается больше частиц, чем на нижнем, температура получается отрицательной. Но насколько согласуется такое определение температуры с математическими основами термодинамики?