Концепция плаща-невидимки может помочь двигаться в жидкости без сопротивления

Рис. 1. Схема устройства для достижения идеальной обтекаемости (нулевое сопротивление и отсутствие характерного следа). Сферический объект радиуса а, непроницаемый для жидкости, укрыт концентрической оболочкой радиуса b из пористого материала. Стрелками внизу показано направление течения жидкости. Рисунок из обсуждаемой статьи в Phys. Rev. Lett.

После появления модели плаща-невидимки обнаружилось, что концепцию, лежащую в основе работы этого устройства, можно использовать также для проектирования «плащей» иного типа — маскирующих объекты от звуковых волн, волн на поверхности жидкости, землетрясений (сейсмических волн) и распространения тепла. Применив эту концепцию, американские физики-теоретики предложили модель устройства, с помощью которого объекты могут двигаться в жидкости без сопротивления, не оставляя при этом за собой характерного следа.

В физике довольно обыденна ситуация, когда подход, используемый для математического описания одного явления, затем применяют или пытаются применить для решения совершенно иных физических проблем. Например, идеи, лежащие в основе микроскопической теории сверхпроводимости, были успешно приспособлены для решения некоторых задач в физике элементарных частиц (см.: Нобелевская премия по физике — 2008, «Элементы», 10.10.2008).

Другой пример — теория суперструн, математический аппарат которой специалисты пытаются задействовать для описания физики конденсированного состояния вещества, в частности для объяснения высокотемпературной сверхпроводимости (см.: Идеи теории суперструн находят применение в физике конденсированного вещества, «Элементы», 08.07.2008).

Один из последних примеров такого плодотворного влияния — концепция плаща-невидимки. Плащом-невидимкой называют устройство, которое делает невидимым какой-либо объект для всего или для изначально заданного диапазона электромагнитных волн вне зависимости от того, под каким углом (углом обзора) эти волны «освещают» укрываемый предмет.

Его реализация стала возможной благодаря искусственно созданным анизотропным материалам (так называемым метаматериалам). Магнитная и электрическая проницаемости этих метаматериалов должны распределяться внутри них так, чтобы электромагнитная волна при попадании в такую среду «обходила» укрываемый объект, а затем восстанавливала свое первоначальное направление и свойства. В результате у стороннего наблюдателя, который принимает электромагнитное излучение, складывается впечатление, будто в процессе распространения волна никаких препятствий на своем пути не встречала.

Непосредственный расчет распределения электрических и магнитных свойств метаматериала, из которого конструируется плащ-невидимка, представляет собой поиск преобразования, трансформирующего декартову систему координат в такую систему координат, в которой огибающие траектории движения лучей излучения станут прямыми линиями, а укрываемая от посторонних глаз область просто-напросто исчезнет. Результатом этого поиска будут коэффициенты, связывающие старые декартовы координаты с новыми.

Далее с помощью системы уравнений Максвелла (они характеризуют электрические и магнитные свойства электромагнитных волн, движущихся в каком-либо веществе) на основе найденных коэффициентов вычисляются необходимые значения диэлектрической и магнитной проницаемостей вещества плаща-невидимки. Иными словами, формулы, описывающие преобразование одной (декартовой) системы координат в другую, позволяют определить желанное распределение электромагнитных характеристик метаматериала, двигаясь через который лучи будут обходить область, где находится объект.

Поскольку создание плаща-невидимки — это фактически математическая задача, очевидно, что не существует каких-либо ограничений на использование этого метода в других областях физики, где фигурируют волновые процессы — например, распространение звука или тепла. Единственная поправка, которая должна быть сделана при данном переходе, — это соответствующее уравнение, которое поможет правильно интерпретировать свойства необходимого метаматериала. Скажем, если речь идет о звуковых волнах, то вместо уравнения Максвелла должны быть уравнения акустики; для теплового процесса необходимо использовать уравнение теплопроводности и т. д.

И действительно, спустя год после публикации статьи с описанием схемы создании плаща-невидимки для электромагнитных волн, начали появляться теоретические работы, в которых рассчитывались свойства метаматериалов для укрытия объектов от звуковых волн.

Дальше — больше. Появились предложения использовать концепцию плаща-невидимки для конструирования метаматериалов с возможностью регулировать направление теплопередачи. Кроме того, были рассчитаны свойства метаматериала, который может помочь избежать разрушительного воздействия сейсмических волн.

Наконец, с помощью идей, лежащих в основе плаща-невидимки, на практике была реализована конструкция, укрывающая объект от волн на поверхности жидкости.

Вдохновленные этими примерами, американские физики-теоретики в своей статье предложили модель устройства, которое управляет потоками движущейся жидкости так, что тело, в ней находящееся, обладает идеальной обтекаемостью (не оставляет за собой характерный след) и, как следствие, имеет нулевое сопротивление при движении в жидкой среде.

Для достижения этого эффекта ученые окружили объект специальной пористой средой (рис. 1). По замыслу авторов статьи, эта среда должна пропускать через себя жидкость таким образом (и, соответственно, иметь такие свойства), чтобы структура течения жидкости не менялась после прохода через пористое вещество.

Здесь четко просматривается аналогия с плащом-невидимкой. Вместо метаматериала для плаща-невидимки — фотонных кристаллов и split-ring-контуров (массива крошечных, порядка длины волны микроволнового излучения, резонансных контуров с разрезами) — имеет место свой метаматериал — пористая среда, а силовые линии электромагнитного поля, которые специально искажаются метаматериалом так, чтобы их направление и плотность до и после прохода через плащ-невидимку были одинаковыми, теперь заменяются линиями потока жидкости. Задача авторов статьи состояла в нахождении таких параметров пористой среды (метаматериала), которые бы удовлетворили сформулированным выше условиям, то есть чтобы среда таким же образом деформировала линии потока.

Для решения этой проблемы ученые вооружились системой уравнений Бринкмана—Стокса, которая описывает течение жидкости в пористой среде. Эта система представляет собой комбинацию уравнений Навье—Стокса — главных уравнений гидродинамики — и закона Дарси, который характеризует процесс фильтрации жидкости через пористую среду.

Чтобы упростить дальнейшие вычисления, авторы статьи рассматривали непроницаемый для жидкости (для моделирования решено было выбрать воду) объект сферической формы радиуса a, который был окружен концентрической проницаемой пористой оболочкой с внешним радиусом b = 1 мм (рис. 1).

Еще одно упрощение касалось характера течения воды, в частности предполагалось, что оно является ламинарным, то есть, грубо говоря, в жидкости не образуются вихри (линии потока не завихряются). Более того, число Рейнольдса (безразмерный параметр, характеризующий течение жидкости, ламинарное оно или турбулентное) считается порядка 1. Иными словами, течение очень спокойное и не предвещает перехода в турбулентный режим (критическое значение числа Рейнольдса, при котором происходит переход от ламинарного течения к турбулентному, для такой геометрии составляет порядка 1000).

Если для плаща-невидимки рассчитываемыми свойствами метаматериала были диэлектрическая и магнитная проницаемость, то теперь ученым предстояло рассчитать такую характеристику среды, как пористость — безразмерный коэффициент, значение которого меняется от 0 (поры в материале полностью отсутствуют) до 1 (абсолютно пористый материал, недостижимая в реальности картина). В уравнении Бринкмана—Стокса этот параметр фактически «регулирует» направление течения жидкости через пористую среду, и потому именно его распределение в данном метаматериале необходимо найти таким, чтобы на выходе из пористой среды линии потока имели такую же структуру, как и на входе.

Численными методами эта задача была успешно решена. На рис. 2 представлено распределение радиальной и азимутальной компоненты коэффициента пористости искомого метаматериала для разных значений числа Рейнольдса.

Рис. 2. Распределение радиальной (вверху) и азимутальной (внизу) компоненты коэффициента пористости внутри материала для достижения идеальной обтекаемости. Координаты оболочки по оси абсцисс приведены в единицах радиуса сферического объекта. Коэффициент пористости измеряется в относительных единицах. Цвет каждой кривой соответствует распределению коэффициента пористости для данного числа Рейнольдса (скорости течения воды). Рисунок из обсуждаемой статьи в Phys. Rev. Lett.

На приведенных графиках нетрудно заметить, что коэффициент пористости почти во всей среде отрицательный, что как бы противоречит заявленному выше утверждению о положительности данной характеристики. Тем не менее полученное решение не противоречит здравому смыслу, если рассматривать пористый материал как активную среду, использующую энергию извне, чтобы ускорять или тормозить текущую через нее жидкость. С точки зрения технической реализации пористая среда должна иметь внутри себя миниатюрные насосы, которые бы стимулировали течение и компенсировали заданным образом градиенты давления, возникающие из-за перепада скоростей в пористой области. Стоит заметить, что такие микронасосы уже существуют (см. Zilin Chen, et al., 2005 и H. T. G. van Lintel, et al., 1988), так что предложение авторов не выглядит таким уж фантастическим.

Теперь на основе вычисленного распределения коэффициента пористости можно продемонстрировать, как жидкость будет двигаться через пористый метаматериал (рис. 3).

Рис. 3. Структура течения воды (линии потока) вблизи и внутри пористой среды и распределение скорости (шкала показана справа) для числа Рейнольдса, меньшего 0,5 (a), равного 2,5 (b) и равного 4,5 (с). Белая область — это укрываемый объект. Рисунок из обсуждаемой статьи в Phys. Rev. Lett.

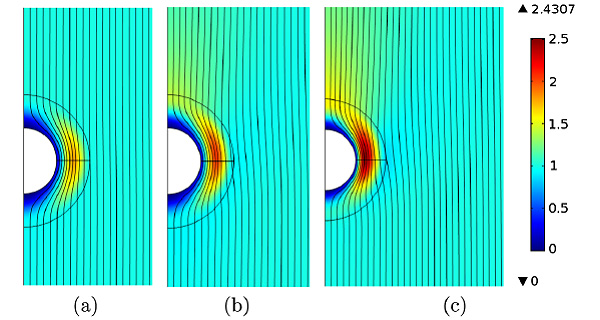
Как видно, линии потока жидкости на выходе из пористой среды имеют ту же структуру, что и на входе. Полученный профиль обтекания указывает на то, что для совсем малых (меньше 1) значений числа Рейнольдса тело не оказывает движущейся жидкости какого-либо сопротивления: сопротивление практически равняется нулю (рис. 3а). Однако по мере увеличения числа Рейнольдса (фактически — скорости жидкости) результаты уже не столь впечатляющие. Для числа Рейнольдса равного 2,5 пористый метаматериал понижает силу сопротивления в 6 раз (по сравнению с тем, когда сфера не укрыта пористым метаматериалом), а для числа Рейнольдса 4,5 это уменьшение составляет скромные 50%.

Для больших значений числа Рейнольдса анализ не проводился, поскольку используемый авторами статьи подход для решения задачи не позволяет с необходимой точностью просчитывать уравнения Бринкмана—Стокса. По мере увеличения числа Рейнольдса изменяется и характер линий потока после обтекания тела — за телом начинает формироваться характерный след. Таким образом, эффективно «спрятать» объект от движущейся жидкости можно лишь для чисел Рейнольдса, значения которых не превышают 2,5.

Тем не менее ученые надеются, что предложенная ими идея использовать пористую среду для уменьшения силы сопротивления при движении тела через жидкость и ликвидации или уменьшения характерного следа может найти разнообразные применения в гидродинамике.

Источник: Yaroslav A. Urzhumov, David R. Smith. Fluid Flow Control with Transformation Media // Phys. Rev. Lett. 2011. V. 107, 074501.

Юрий Ерин