В поисках универсального закона устройства биологических сообществ, или Почему экологи потерпели неудачу?

В любом природном сообществе (будь то планктон озера, деревья тропического леса или совокупность птиц, обитающих на определенной территории) всегда можно найти несколько видов массовых, доминирующих по численности и гораздо большее число видов редких, малочисленных. Если у нас имеется большая (в несколько тысяч особей) проба из сообщества, то, разбив все обнаруженные в ней виды на классы обилия и определив число видов в каждом классе, мы можем построить гистограмму распределения частот встречаемости видов разной численности. График, проведенный по вершинам столбиков гистограммы, представляет собой сильно вогнутую кривую, напоминающую гиперболу. Подобный результат, выявляемый при анализе практически любого сообщества, на самом деле не очевиден и нуждается в объяснении. Кажется, более естественным было бы ожидать преобладания в природе видов, имеющих какую-то среднюю численность, при гораздо меньшем числе видов редких или, наоборот, массовых. Хотя проблема изучается уже более полувека, удовлетворительного объяснения наблюдаемой картины соотношения численностей разных видов пока нет. По мнению Брайена Макгилла (Brian J. McGill) c биологического факультета Университета Макгилла (Монреаль, Канада) и его соавторов, ситуацию, сложившуюся в изучении структуры сообществ, можно охарактеризовать как «коллективную неудачу» (collective failure). Выводы этого исследования, опубликованные в журнале Ecology Letters, могут быть поучительными не только для неудачливых экологов, но и всех, кому приходится сталкиваться с отсутствием прогресса в решении той или иной научной проблемы.

Выдающийся американский эколог Джордж Эвелин Хатчинсон (G. Evelyn Hutchinson, 1903–1991) одну из своих статей, вышедшую в 1959 году, назвал «Дань Святой Розалии, или Почему так много видов животных?» (Homage to Santa Rosalia, or why are there so many kinds of animals?, PDF, 30 Кб). В маленьком прудике около церкви Св. Розалии на горе Монте-Пеллегрино около Палермо (Сицилия) он обнаружил двух водяных клопов одного рода, но различающихся размерами. Рассуждения о том, как виды могут сосуществовать несмотря на конкуренцию, привели Хатчинсона к постановке важных вопросов о том, что определяет видовую структуру сообществ. Однако проблема соотношения численностей разных видов в сообществе имеет на самом деле куда более давнюю историю.

Так, еще в 1932 году появилась работа японского исследователя Мотомуры, предложившего модель, согласно которой виды одного сообщества, ранжированные по убыванию численности, используют одну и ту же долю оставшегося общего ресурса. Например, если самый многочисленный вид потребляет 70% ресурса (и соответственно, такова его численность), то второй вид потребляет 70% того, что осталось от первого, следующий по убыванию численности вид — 70% от того, что осталось после первого и второго, и так далее. Через 25 лет американский эколог, ученик Хатчинсона Роберт Макартур (Robert MacArthur), используя сходную логику, предложил свою «модель разломанного стержня» (brocken stick model), в которой лимитирующий ресурс (одномерное пространство ниши) моделировался стержнем, случайным образом разломанным в разных местах. Численности видов были пропорциональны длинам образовавшихся отрезков. Хотя модель Макартура удовлетворительно описывала соотношения численностей разных видов птиц, сам автор позднее признал ее в теоретическом отношении несостоятельной.

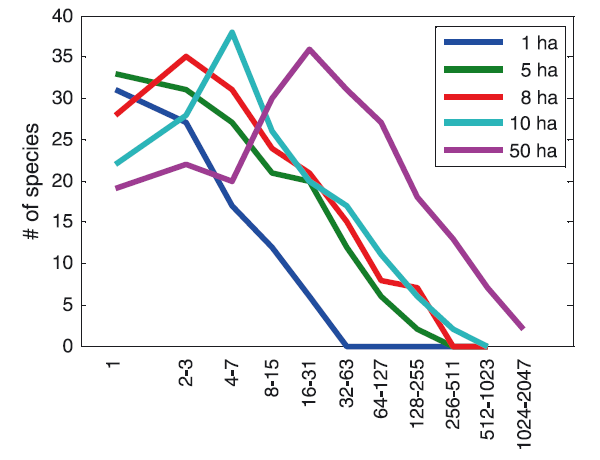
Совершенно другой подход к решению проблемы видовой структуры сообщества использовал известный специалист по математической статистике Рональд Фишер (Ronald Fisher). Работая на Ротамстедской экспериментальной станции (Rothamsted Experimental Station) в Англии, он помог энтомологам А. Корбету и К. Уильямсу статистически обработать результаты отлова ночных бабочек с помощью световых ловушек. Фишер предположил, что распределение числа видов бабочек, имеющих разную численность, лучше всего описывается логарифмическими сериями (Fisher, Corbet, Williams, 1943). Максимальное число видов, согласно модели Фишера, приходится на категорию самых редких, представленных в пробах порой всего одним-единственным экземпляром. Чуть позднее появилась работа американского исследователя Ф. Престона, который использовал логарифмические классы обилия — «октавы», как он их называл. В первую октаву входили виды, представленные в выборке одной особью, во вторую — двумя особями, в третью — 3-4, в четвёртую — 5-8, в пятую — 9-16 и так далее (см. такую шкалу на рис. 4 и 5). Гистограмма соответствующего распределения напоминала классическую Гауссову кривую нормального распределения. Иными словами, распределение оказалось логнормальным: самых редких видов было всё же меньше, чем слегка более многочисленных. Престон полагал, что все достаточно большие выборки из сообщества должны описываться логнормальным распределением. Если же проба недостаточна репрезентативна, то левая часть кривой нормального распределения («хвост» редких видов) оказывается отрезанной.
Макгилл и его соавторы (17 исследователей из 7 стран), проанализировав огромный массив литературы по проблеме видовой структуры сообществ, выявили более сорока моделей, описывающих соотношение численностей разных видов. Эти модели различались принципами устройства. Одни сводились к поиску математического распределения, которое бы удовлетворительно описывало некий набор эмпирических данных. Другие исходили из того, что особи размножаются, и, соответственно, можно использовать модели, основанные на теории ветвящихся процессов (branching processes). Третьи апеллировали к представлениям о динамике численности популяций. А были и такие, которые основывались на пространственном распределении видов или на том, как может делиться общий, ограничивающий всех ресурс (примеры последней категории — модели Мотомуры и Макартура).

Однако, несмотря на столь большое число разных моделей, все они более или менее удовлетворительно демонстрировали один и тот же результат, а именно — «вогнутую кривую» (то есть распределение, характеризующееся множеством редких видов и очень малым числом видов массовых). Вряд ли такой результат можно считать существенным достижением, особенно учитывая ту огромную работу, которая была проделана множеством экологов уже не одного поколения. Скорее — это «коллективная неудача» (collective failure), причина которой, по мнению авторов обсуждаемой статьи, в том, что не были соблюдены методические установки, обеспечивающие научный прогресс. Совокупность таких установок, или «правил», Джон Платт (Platt, 1964) в свое время назвал «строгим выводом» (Strong inference). Апеллируя к этой старой, но вовсе не утерявшей своего значения работе Платта, Макгилл и его соавторы формулируют своего рода уроки прошлого — несколько ключевых положений, которые обязательно должны быть учтены, если мы хотим добиться прогресса в познании видовой структуры сообществ:
(1) Конкуренция гипотез. Ситуация была таковой, что новые гипотезы предлагались, а старые не отвергались. Модели не сравнивались между собой по результатам, то есть по тому, насколько хорошо они описывают реальность. Конкуренция гипотез отсутствовала.
(2) Множественные механизмы. Экологи порой забывали, что сходство паттернов (выявляемых регулярностей) вовсе не означает обязательного сходства процессов, которые могут их порождать. Да и в математике одна структура может быть получена разными путями.
(3) Решающие свидетельства. Нередко предсказания разных моделей столь мало между собой различались, что сравнивать их было очень сложно. Если какая-то модель удовлетворительно объясняет 99,1% вариации реальных данных, а другая только 99,0% — можем ли мы утверждать, что первая модель действительно лучше? Ведь статистическая ошибка тех данных по природным сообществам, которые имеются в нашем распоряжении, весьма велика, значительно больше различий, даваемых разными моделями.
(4) Робастные оценки. Суждения о преимуществе той или иной модели должны основываться на робастных оценках, то есть устойчивых при использовании разных критериев.
(5) Применимость модели по отношению к разным множествам данных. Нередко определенная модель хорошо описывает одну группу данных, но плохо описывает другую. Конечно, можно думать, что механизмы, ответственные за формирование структуры сообщества деревьев, отличны от механизмов, формирующих сообщество рыб. Но когда речь идет об участках тропического леса на разных континентах, то правило бритвы Оккама («не следует множить сущее без необходимости») заставляет нас ожидать сходных процессов.
Несмотря на общий критический настрой обзора Макгилла и др., в нём есть и оптимистичные ноты. Универсальность «вогнутой кривой» и ее возможная связь с разными макроэкологическими процессами, проявляющимися на больших совокупностях разных видов, населяющих крупные территории и акватории, позволяет надеяться на то, что в конце концов будет сформулирована некая объединяющая экологическая теория. Авторы статьи подчеркивают, что от теории в экологии не следует ожидать прогнозов, возможных в физике (например, таких, как столь любимый известным методологом науки Имре Лакатосом пример предсказания существования Нептуна по отклонениям орбиты Урана). Они разделяют мнение Розенцвейга и Абрамского (Rosenzweig, Abramsky, 1997), которые полагают, что не только теория видовой структуры сообщества, но и вся экология продвигаются вперед посредством не радикальной смены парадигм, а, скорее, методом, который они окрестили «dipswitch testing».
DIP-переключатель (Dip switch) — это набор связанных переключателей, которым еще недавно пользовались при настройке компьютеров (DIP, dual-in-line package — корпус с двухсторонним расположением выводов). Фактически, логика подхода «dipswitch testing» сводится к тому, что экологи могут давать множество бинарных предсказаний типа «Y возрастает, если возрастает X». Одно такое бинарное предсказание с вероятностью 50 на 50, конечно, очень слабое, но если какая-то модель (гипотеза) дает множество таких качественных (но проверяемых) предсказаний, то мы вправе считать данную модель хорошей.
Макгилл и его соавторы призывают экологов рассматривать проблему структуры сообщества не изолированно, а в более общем контексте, в частности изучать то, как влияют на структуру абиотические факторы, как проявляется структура на разных трофических уровнях или как на ней сказывается распространение заносных, «инвазивных видов» (см.: Invasive species), часто становящихся необычайно массовыми.
Источник: Brian J. McGill, Rampal S. Etienne, John S. Gray et al. Species abundance distributions: moving beyond single prediction theories to integration within an ecological framework (полный текст статьи в открытом доступе) // Ecology Letters. 2007. V. 10. No. 10. P. 995–1015.
См. также:
1) J. R. Platt. Strong inference (полный текст, PDF, 60,2 КБ) // Science. 1964. V. 146. P. 347–353.
2) David Alonso, Annette Ostling, Rampal S. Etienne The implicit assumption of symmetry and the species abundance distribution // Ecology Letters. 2008. V. 11. No. 2. P. 93–105.
3) А. М. Гиляров. От ниш к нейтральности в биологическом сообществе // Природа. 2007. № 11. С. 29–37 (см. полную версию в формате PDF, 6,45 Мб)
4) Конкурирующие виды могут сосуществовать и в одной, и в разных нишах, «Элементы», 20.02.2007.
5) Разнообразие тропических лесов обеспечивают грибы-паразиты, «Элементы», 03.05.2006.
6) Многие интересные работы Макгилла можно получить свободно в виде PDF-файлов на его личной странице.
Алексей Гиляров
-
Странно, чем занимаются эти экологи. Логично было бы исследовать внутрисистемные закономерности экологических сообществ, определяющие численные соотношения видов. А ищут почему-то внешние статистические оценки.
Экологии - они ведь как фабрики: каждый организм имеет своё место и выполняет свою чёткую роль в общем деле - преобразовании низкоэнтропийной энергии в высокоэнтропийную.
Численности видов связаны с этими их ролями в сообществе. Вот и нашли бы эти связи. Получили бы ответы сразу на "почему" и "как". А то ищут только ответ на вопрос "как": найти его вроде проще, но получаемой тут информации недостаточно, чтоб ответить и на "почему".
>как влияют на структуру абиотические факторы
Интересно, например, изучали ли связь спектров размеров "кусочков" ресурса с численностями способных ими питаться видов.-
Прекрасное предложение: "исследовать внутрисистемные закономерности экологических сообществ, определяющих численные соотношения видов". НО КАК ЭТО РЕАЛЬНО СДЕЛАТЬ?
-
Сфокусировать внимание не на количественных характеристиках экосистем, а на качественных, из которых количественные проистекают. Кто как и чем питается, и откуда эта еда берётся. Например, питается белка орехами, орехов понятно сколько растёт, от них зависит её численность. А какая-нибудь птичка не может разгрызть орехи, ест то, чем накрошит белка. Отсюда, численность этой птички на порядок ниже, чем белки - такие у них роли в экосистеме.
Так, между низкоэнтропийным светом, падающим на планету и излучаемым ею теплом, существует сеть преобразований энергии, связанная с контуром преобразования материи, участвующей в энергообмене.
Далее, среди всех экосистем существуют общие, наболее частовстреающиеся пути, вроде плоды->крупные/многочисленные животные, макроскопические остатки плодов->мелкие/малочисленные животные, микроскопические остатки->насекомые и бактерии, частично переваренная органика->бактерии. Плюс вариации отношений хищник-жертва, паразит-хозяин.
Одна из фишек в том (и об этом скользнуло в статье), что природа очень экономна, и любой ничтожный ресурс найдёт своего поклонника. Выедать 100% родного ресурса вид не может, ибо действует эмпирический принцип 20-80: 20% времени тратится чтобы съесть 80% плода/жертвы. Дальнейшее "обгладывание" менее эффективно, чем поиск нового плода/жертвы. Таким образом, всегда имеются излишки, что открывает пространство для возникновения специализирующихся на этих излишках видов.
И вот, выделение подобных общих принципов и построение общих схем ресурсооборота, и величин потоков ресурсов даст системное объяснение распределений численностей видов по экологиям.-
То есть Вы предлагаете изучать потоки энергии по наблюдаемым феноменам (участники экологической системы)?
-
Да, только скорее не просто энергии, а ресурсов (с учётом их качества) и не по, а между наблюдаемыми феноменами. Например, можно построить модель - граф, узлы которого - виды, а дуги - ресурсы. Каждый узел что-то производит и что-то потребляет, в зависимости от численности вида. Численности можгут меняться. Если есть нехватка ресурса, вид начинает потреблять менее выгодный ресурс. То есть, дуги перестраиваются в ходе вычислений. И вот, основываясь на внутрисистемных взаимодействиях и реальных данных по потреблению, такая модель могла бы в динамике порождать реальное распределение численностей, ну и просто демонстрировать особенности реакции экосистем на внешние воздействия и прочия.
-
-
-
Господа, дело в том, что сообщества, структура которых во множестве работ исследуется и представляется в виде частот встречаемости видов, имеющих разную численность, это почти всегда сообщества организмов одного трофического уровня. Деревья тропического леса - их может быть на 50 га до 1000 видов!!! (Борнео), две-три сотни видов - обычное дело. Все они нуждаются в одних и тех же ресурсах (вода, азот, фосфор, свет); как правило, наиболее напряженная конкуренция разворачивается за свет. И вот даже в таком сообществе - много редких видов и мало массовых. И возникает вопрос - а почему эти редкие виды давно не вымерли, почему их не вытеснили более успешные, достигшие куда большей численности. Или почему не преобладают виды, имеющие какой-то средний ранг обилия? И споры идут между сторонниками разных моделей, описывающих (а порой - пытающихся объяснить) наблюдаемый паттерн. В этих вещах, видимо, тесно взаимодействуют процессы конкуренции, процессы расселения и процессы видообразования... Не так все просто. Потому и collective failure!
-
Тогда это скорее вопрос эволюции и генетики. Наверняка у малочисленных видов генетическое разнообразие, нормализованное по численности, ниже, чем у видов, представленных большой численностью. То есть, минорные виды, столкнувшись с вытеснением со стороны более эффективного соседа, ради повышения гарантий выживания "отказались" от большой части нормального генетического разнообразия.
Либо, возможно, в филогенезе существует тенденция к редким бурным вспышкам численности, являющим собой один из этапов динамики видообразования.
Впрочем, когда речь заходит об эволюции, гипотез становится больше, чем способов их устранения... -
Уважаемый Алексей Меркурьевич,
По-моему, обсуждаемое явление можно достаточно легко объяснить, если допустить, что каждый организм, участвующий в пищевой цепочке, порождает определенный 'звук' (излучение), который вливается в общий 'шум толпы' данного экологического сообщества. Я здесь использую аналогию со звуком, чтобы она была понятна большему числу читателей.
Если здесь и есть натяжка, то крайне небольшая - ведь никто не станет отрицать тот факт, что каждый живой организм порождает определенный набор электромагнитных полей (от сверхдлинных волн до ультрафиолета), и нет никакой крамолы в том, чтобы предположить, что каждый организм в той или иной мере 'отслеживает', _в частности_, электромагнитную обстановку вокруг себя. Я не хочу здесь углубляться в детали механизма подобного 'слежения', т.к. это уведет в сторону от основной темы. Достаточно принять, что каждый отдельный организм обладает механизмами как излучения, так и приема окружающей 'полевой' обстановки.
В этом случае экологическое сообщество в данном регионе может быть представлено как сложный 'аккорд', а каждый вид будет 'тянуть', условно говоря, свою ноту в этом аккорде. При этом, однако, все вместе стараются 'петь' так, чтобы аккорд был 'гармоничным'. По сути, я здесь описал что-то вроде метода самосогласованного поля (http://en.wikipedia.org/wiki/Multi-configurational_self-consistent_field), которым пользуются в физике и химии. Если вам не нравится физика-химия - можно придерживаться моей аналогии с хором.
Так вот, если 'хористы' хотят петь что-то гармоничное, они не могут произвольно выбирать ноты, которые 'тянут'. Совершенно очевидно, что очень скоро окажется, что мы имеем несколько довольно больших групп, которые 'задают тон' в общем аккорде, и множество мелких 'подпевал', которые поют что хотят, но не определяют общую картину. При этом соотношение между 'основными певцами' и 'подпевалами' будет определяться тем, насколько 'подпевалы' своим 'шумом' искажают основной аккорд. Опять же, я не вижу смысла углубляться в возможные физические механизмы формирования 'главных нот' этого 'аккорда', чтобы не уходить в сторону. Да и вряд ли кому это будет интересно.
Как видите, привлечение физического подхода (в частности, полевой модели) позволяет предлагать достаточно ясные и логические объяснения там, где традиционные методы приводят к collective failure :)-
Глубокоуважаемый Михаил, мне кажется, что Вы множите сущности сверх надобности. К тому же, нет тут пищевой цепочки. А зачем им "петь гармонично"? Эволюция видов весьма эгоистична и о своем будущем эти виды не "думают"! Я бы все же призвал комментаторов прочесть исходную статью - она ведь в открытом доступе! Кроме того, уже после нее появилась в Ecology Letters статья, предлагающая на все взирать с точки зрения энтропийного принципа (хотя это уже не раз предлагалось и ранее). См.: Salvador Pueyo, Fangliang He, Tommaso Zillio (2007) The maximum entropy formalism and the idiosyncratic theory of biodiversity (http://www.blackwell-synergy.com/doi/full/10.1111/j.1461-02
48.2007.01096.x ). Работа в открытом доступе! А затем уже в этом году там же вышла статья:
David Alonso, Annette Ostling, Rampal S. Etienne (2008) The implicit assumption of symmetry and the species abundance distribution
Ecology Letters V. 11 (2), 93-105 doi:10.1111/j.1461-0248.2007.01127.x
Эта работа не открыта, но можно попросить авторов прислать пдф. Мне не хватает математического образования, чтобы грамотно отразить эти работы в "новостях". Но остается ощущение, что какими-то самыми общими принципами мы всегда все объясним (законы термодинамики конечно работают, закон сохранения вещества выполняется, и естественный отбор идет всегда и везде в обязательном порядке...). Но такие крайне общие объяснения все же не устраивают биологов, и даже многих математиков, работающих с биологическим материалом....-
Уважаемый Алексей Меркурьевич,
Вообще-то я не умножаю сущности сверх меры, а всего лишь пытаюсь учесть дополнительные параметры реального процесса.
Честно говоря, после того, как я посмотрел статью, на которую Вы сослались, у меня возникло ощущение, что активное применение в биологии методов, взятых из статфизики, убивает сущности сверх меры :).
Взять, хотя бы, тот же метод максимальной энтропии, который используется в статье. Да, этот метод позволяет найти наилучшее приближение кривой, описывающей распределение вероятностей, но он НИЧЕГО не говорит нам о природе процессов, которые приводят к такому распределению. Само по себе наличие видов, распределенных каким-то образом, предполагается уже заданным Господом Богом, и мы всего лишь пытаемся угадать, в каком настроении был Бог, когда рисовал эту кривую.
Ведь, насколько я понимаю, основной вопрос в обсуждаемой статье - не в том, почему КРИВАЯ выглядит именно так, а почему в природных условиях ВЫГОДНЕЕ, чтобы в данной экосистеме существовал, допустим, 1 вид птиц численностью 1000 особей и 20 видов практически таких же птиц численностью от 20 до 100 особей, которые делят с главным видом ОДНУ И ТУ ЖЕ пищевую цепочку. Как я понял, биологи задают совершенно естественный вопрос - если эти 20 видов все-таки делят с главным видом одну и ту же пищевую цепочку, то почему мы не наблюдаем более-менее РАВНОЕ распределение численности этих видов? Что МЕШАЕТ этим субдоминантным видам размножиться до такой же степени, что и доминантный? Если я неправильно понимаю проблему - пожалуйста, поправьте меня.
Так вот, статья, на которую Вы сослались, объясняет, почему разные ОПИСАНИЯ биосистем дают практически один и тот же результат. Но она НИЧЕГО не говорит (и ее авторы, естественно и не собирались говорить) о том, какова ПРИРОДА процессов, описываемых той или иной моделью. Ведь когда вы перешли к вероятностям (т.е. построили модель), вы УЖЕ убили всю информацию о физической природе процесса, ибо вероятность - величина безразмерная...
Моя же модель описывала именно МЕХАНИЗМ возникновения кривой распределения и отвечала на вопрос, ПОЧЕМУ в конце концов в каждой пищевой цепочке будет возникать доминирование небольшого количества видов. При желании эту модель можно довести и до математической формулировки, но, зная 'дружбу' биологов с математикой, я и не предполагал это делать.-
С началом Вашего комментария (касательно того, что распределение, взятое из статфизики, ничего не говорит о природе процессов) я полностью согласен. А вот насчет ВЫГОДЫ не уверен. Виды (растений, животных, грибов, бактерий) вовсе не готовы "жертвовать своим благом во благо" всего сообщества, а тогда и им будет хорошо. "Жила бы страна родная и нету других забот". Эта точка зрения была раньше довольно популярна, но сейчас ясен эгоистичный характер каждого вида. В этом смысле удачно название книги Докинза (Dawkins) Эгоистичный ген The Selfish Gene. Поэтому слово ВЫГОДНЕЕ нуждается в пояснении - для кого, для чего выгоднее! Поэтому возникновение альтруизма (в пределах ОДНОГО вида) потребовало непростых объяснений.. Но умница Билл Гамильтон (W.D.Hamilton - см.: http://en.wikipedia.org/wiki/W._D._Hamilton ) с этим справился (жаль, что он так рано умер, один раз мне посчастливилось с ним беседовать).
-
А я и не говорил о том, что вид 'заботится' о выгоде сообщества в целом. Разумеется, речь идет только о 'личной выгоде' вида. Точнее было бы, наверное, говорить о минимуме энергозатрат.
Так вот, если говорить в рамках аналогии с пением в хоре, то каждый организм (от клетки до высших млекопитающих) постоянно 'слушает' окружающее 'пение' и старается 'попасть в тон' с ближайшей нотой. Сам механизм такой 'подстройки' имеет весьма древнюю эволюционную природу и, очевидно, выгоден индивидууму: ведь, находясь 'вблизи' доминирующего состояния, он автоматически попадает в зону экологического оптимума, т.е. наилучшей адаптации к условиям окружающей среды. При этом сам оптимум формируется из состояний всех родственных (а может, и не только родственных) организмов, обитающих в данной среде, и, соответственно, учитывает наиболее характерные особенности этой среды.
Также становится очевидным, что популяции в целом НЕВЫГОДНО поддерживать большое разнообразие 'нот' (доминирующих состояний), т.к. это приведет к тому, что индивидуальные организмы будут вынуждены постоянно перенастраиваться с одной 'ноты' на другую, а биологические системы в этом отношении весьма консервативны. Поэтому популяции в целом гораздо выгоднее найти какое-то одно стабильное или достаточно медленно меняющееся состояние и держаться вблизи него, пока не возникнут более-менее веские причины для перехода в другое состояние.-
-
Михаил, как я понимаю, пытается говорить о межвидовой (и внутривидовой) коммуникации и о сигнальных полях (sensu Наумов). Различия и избирательность реакции на разные элементы сигнального поля вполне может определять как плотность населения, так и пространственную структуру популяций.
Ну и кроме того, интересно посмотреть не просто связь обилия видов с их численностью, а включить в модель ширину экологических ниш и естественную временную и пространственную динамику условий, позволяющих этим нишам реализоваться. Неплохо было бы сравнить также зависимость обилие/разнообразие в рудеральных сообществах и климаксных.
Гложут меня смутные сомнения, что основным фактором collective failure являются не столько пять перечисленных факторов, сколько количество сил, денег и времени потребных для экологического описания феномена. Вовлеченность в такого типа исследования резко снижает число публикаций в единицу времени и, соответственно, число последователей.
Последствия в условиях современной наукометрии понятны :))
-
-
-
-
-
-
-
-
-
Это были статические (срезы ситуаций) модели или динамические? Реальное отображение ресурсовых задач всегда динамическое.
-
Даже не просто динамические, а динамические в квадрате. Моделировались системы управления, основанные на имитации естественных генно-белковых СУ, и эксперимент проходил как чередование этапов собственно управления (в динамике) и этапов изменчивости СУ, пока в результате постоянного отбора не выявлялись оптимумы эффективности управления.
-
-
-
-
-
-
-
но ссылаться на материалы исследований многовидовых сообществ тропических деревьев не совсем справедливо. Да, виды деревьев используют общие воду, углекислоту, фосфор и пр. но эти ресурсы распределены в почвенном коллойде и количественно ограничены. Корни растений так или иначе пространственно делят толщу почвы, пусть даже корневые волоски все рядом стоящих деревьев будут вырастать, тесно соприкасаясь друг с другом, те речь на самом деле идет о разделенном ресурсе. И фактически исследователи имеют дело с живыми деревьями, которые УЖЕ усвоили требуемое количество вещества и света и продолжают это делать. Дерево умирает, падает, освободившийся просвет, пространство почвенного коллойда и вещества поступающие от него в опад занимает другое растение, оказавшееся в нужное время на месте, которое в это время как и другие особи его вида где-то сохранялось, в виде семени ли, подроста, это не так важно. Важно что у вида были для этого возможности-ресурсы, была для этого своя часть среды. Таким образом, возможно это просто одна из очередных апеляций при рассмотрении важных общих вопросов к не до конца осмысленным данным полевых исследований.
Я занимаюсь сходными вопросами на примере жвачных, а точнее на примере растительных сообществ, анализируя их количественно в контексте диет, Жвачные не смотря на родство и сходство в диетах тем не менее попарно больше чем на 60% по видам поедаемых растений не перекрываются. Те у каждого потребителя есть свой, ни кем из ближайших сопеников не способный быть освоенным резерв в общей массе растительности. Структура гильдий жвачных более предсказуема на основе представлений о нише. Может быть если скурпулезно разобраться в других ярких и часто используемых примерах сообществ, то выйдет что есть ресурсы общие, вокруг которых группируются виды, скореее всегог временно и есть ресурсы, которые дают им выжиить, когда общий ресурс истощен. Я конечно не претендую на безоговорочность
Последние новости













