Автомобильные пробки: когда рациональность ведет к коллапсу
А. Гасников, Ю. Дорн, Е. Нурминский, Н. Шамрай
«Квант» №1, 2013
Введение
Когда мы только начинали писать эту статью, нам на глаза попался прекрасный слоган в одной социальной рекламе: «Вы не застряли в пробке. Вы и есть пробка». Мало кто из водителей, стоящих в пробке, задумывается о том, что он сам становится причиной задержки тех людей, кто едет вслед за ним, а даже если и задумывается, то не придает этому большого значения. При этом, подрезая очередную машину, водители жалуются на то, как мало строится дорог.
Еще в XVIII веке британский экономист Адам Смит посеял в умах ученых и общественных деятелей увлекательный образ сообщества независимых экономических агентов — потребителей и производителей, каждый из которых, действуя в своих интересах, в результате создает эффективное общественное производство. Можно сказать, что это было первой редакцией лозунга «Анархия — мать порядка!». Однако еще раньше другие, не менее выдающиеся, умы человечества горестно отметили печальное исключение из этого правила — то, что эколог Хардин удачно окрестил «трагедией общей собственности».
Это значит следующее. Если некоторый ресурс находится в общей собственности и для его использования нет никаких ограничений, то он будет подвергаться чрезмерной эксплуатации и исчезнет. Стеллерова корова или почти исчезнувшее Аральское море тому наглядные примеры, и этот горестный список можно продолжить. Экономисты описывают «трагедию общей собственности» как такой вариант общественного устройства, когда с точки зрения отдельного потребителя выгоды от потребления ресурса достаются ему одному, а негативные последствия делятся на всех. В современном мире одним из таких ресурсов являются автомобильные дороги, а «синие мигалки» — наиболее яркое тому свидетельство, усугубленное узурпированным преимущественным правом некоторых пользователей на этот ресурс. Но и независимо от наличия или отсутствия «мигалки» каждый новый автомобиль на дороге приносит своему владельцу определенную пользу или удовлетворение, а негативные последствия — возрастающая плотность автомобилей, замедление движения, заторы и пробки — делятся на всех. Для принципиального выхода из этой ситуации нужна целая система мер, которые примирили бы эгоистическое поведение водителей и общественную пользу, но это слишком обширная тема, для знакомства с которой можно порекомендовать общедоступную книгу В. Вучика «Транспорт в городах, удобных для жизни» (“Transportation for Livable Cities”). Но в любом случае, когда ученые собираются что-то советовать, то они прежде всего изучают явление и определяют, как на него повлияют разные воздействия. В данном случае наиболее видимым и огорчительным являются уличные пробки. Так что же такое пробки и как с ними бороться?
Откуда берутся пробки
Вообще говоря, прежде нужно понять, что такое пробка. Некоторые водители говорят о пробке, когда им приходится ехать со скоростью 20 км/ч из-за плотного движения, вместо желаемых 100 км/ч. Другие же подразумевают под пробкой почти глухой затор. Оба эти случая имеют общую природу — слишком много автомобилистов решили использовать одну и ту же дорогу. Все упирается в то, что понимается под «слишком много».
Можно было бы указывать на то, что у каждой дороги от перекрестка до перекрестка есть вполне конкретные ширина и длина и там «физически» не может поместиться слишком много автомобилей. Но этого аргумента недостаточно, ведь важна еще скорость движения. Если бы водители могли практически без зазоров между машинами ехать на скорости 1000 км/ч, то пропускная способность любой дороги была бы почти неограниченной. Ответ в том, что движение на дороге определяется тем, какие решения принимают водители. Для большинства из них «некомфортно» ехать на скорости 100 км/ч в режиме «бампер к бамперу» — слишком велики риски повредить автомобиль или попасть в крупную аварию. Например, в США еще в школах вождения учат «правилу 3 секунд» — поддерживайте между собой и впереди идущей машиной расстояние, которое вы на данной скорости проедете за 3 секунды. В непогоду это время рекомендуют утраивать. Нечего и говорить о том, что это правило написано кровью тех водителей, которые его не выполняли... Любопытно, что если при этом пренебречь собственными размерами автомобилей, то их поток, т. е. количество автомобилей, пересекающих за единицу времени некоторую контрольную линию, не зависит от скорости и составляет 1200 автомобилей в час на одну полосу движения, что считается нормативной пропускной способностью дороги. Если учесть собственные размеры автомобиля, то пропускная способность существенно уменьшается, особенно при малых скоростях. Но это следует из простейших моделей движения автомобилей, в реальности нужно учитывать массу других факторов, одно перечисление которых может занять не одну страницу. Поэтому ограничимся хорошо установленным экспериментальным фактом — средняя скорость движения на дороге зависит от плотности автомобилей, т. е. их количества на единицу длины дороги, в качестве которой обычно рассматривается километр. При этом чем больше плотность, тем ниже скорость. В простейшем случае предполагается линейная зависимость между плотностью R и скоростью ![]() :
:
R(![]() ) = –a
) = –a![]() + R0,
+ R0,
где a — некоторая константа.
Эта модель была предложена американским инженером-транспортником Брюсом Гриншилдсом (Bruce Greenshields) в 1933 году и до сих пор широко используется в системах моделирования дорожного движения! Недавно в ее честь был даже проведен международный симпозиум, отметивший 75-летие первой публикации. Причина такого внимания к этой модели заключается в том, что она впервые ввела понятие фундаментальной диаграммы поток–скоростьи продемонстрировала наличие максимального потока. Действительно, если мы определим поток Q(![]() ) автомобилей в единицу времени как произведение R
) автомобилей в единицу времени как произведение R![]() , то
, то
Q(![]() ) = –a
) = –a![]() 2 + R0
2 + R0![]() ,
,
и график этой квадратичной функции (рис. 1) имеет максимум в точке ![]() = R0/(2a).
= R0/(2a).

С тех пор предложена масса модификаций этой зависимости, но сама концепция фундаментальной зависимости поток–скорость остается в основе большинства моделей, как и понятие максимального потока, который может обслужить дорога в единицу времени. Когда на дорогу в единицу времени начинает въезжать больше автомобилей, чем ее пропускная способность, начинает образовываться пробка. Собственно говоря, при этом модель Гриншильдса перестает быть применимой и начинается нерасчетный режим.
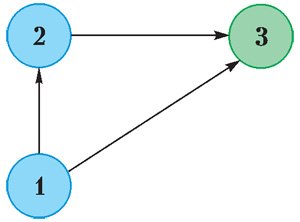
Представьте себе перекресток 1 (рис. 2) и два маршрута, по которым можно доехать до пункта назначения в вершине 3. Причем дорога (1,3) — «короткая», а путь через вершину 2 — длинный объезд. Пусть дорога (1,3) будет двухполосной. В центре дороги (1,3) одна из полос закрыта не ремонт. В начальный момент времени, когда обе дороги пустые (например, в 5 утра), все водители, желающие доехать из 1 в 3, воспользуются дорогой (1,3). Если одна полоса может обслужить 1500 авт./ч, а на дорогу в какой-то момент начнет поступать поток в 2500 авт./ч, встанет вопрос — куда денутся 1000 авт./ч? Конечно, встанут прямо перед узким местом. Более того, из-за необходимости перестраиваться, по работающей полосе поток будет ниже 1500 авт./ч. С течением времени пробка будет расти. Вопрос номер два — когда пробка расти перестанет? Логика и законы сохранения нам подсказывают, что это случится, если количество въезжающих на дорогу водителей сравняется с количеством выезжающих, т. е. станет примерно 1500 авт./ч. Но куда денутся лишние 1000 авт./ч, ранее использовавшие данную дорогу в своем маршруте? Очевидно, начнут (из-за пробки) использовать объезд. Переключение на объездную дорогу произойдет ровно в тот момент, когда водителям будет безразлично, какой из маршрутов (короткий или объездной) использовать. Но ведь если бы объезд использовался с самого начала, пробки бы не возникло! Водителей можно понять, кому же захочется ехать в далекий объезд, если рядом короткая дорога, и пусть она работает на пределе, но уж мы как-нибудь прорвемся (а за нами хоть потоп!). Вот так и начинается пробка.
Модель
В дальнейшем мы рассмотрим модель для описания поведения водителей и транспортной системы в целом на конкретном примере. Сеть, изображенная на рисунке 3, обычно используется для иллюстрации так называемого парадокса Брайеса.
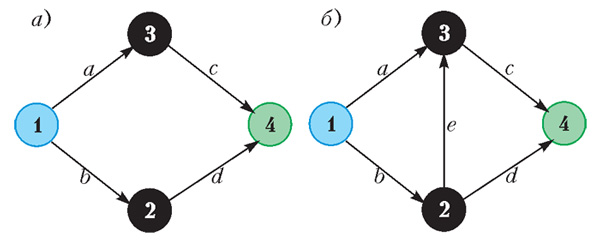
На время забудем о рисунке 3,б (он понадобится нам позднее) и будем работать только с графом на рисунке 3,а.
Городская транспортная сеть задается взвешенным ориентированным графом Г(V, E, T), или, говоря проще, дороги представляются ребрами графа, они имеют заданное направление (поэтому граф направленный, т. е. ориентированый), перекрестки — вершины графа, при этом каждому ребру соответствует определенное время, которое водитель должен потратить на проезд. Это время и является «весом» ребра (поэтому граф взвешенный). Здесь V — множество вершин графа (множество перекрестков), на рисунке 3,а они обозначены цифрами 1, 2, 3 и 4, а E — множество ребер графа (дороги), на рисунке 3,а дороги обозначены буквами a, b, c и d. Каждой дороге соответствует свой «вес», который, вообще говоря, зависит от того, сколько людей эту дорогу использует. Понятно, что чем больше машин использует какую-то конкретную дорогу, тем больше пробка и тем больше времени потребуется на проезд. «Вес» дороги описывает зависимость времени на проезд по ребру от того, сколько автомобилей его использует. Обозначим функции весов дорог через fa, fb, fc и fd для ребер a, b, c и dсоответственно.
В нашем модельном примере мы будем считать, что у всех ребер функции весов линейные, в частности, fa(t) = fd(t) = 50 + t, fb(t) = fc(t) = 10t. Еще раз поясняем, что, например, запись fd(t) = 50 + t следует понимать примерно так: если по дороге d едет t водителей в единицу времени, то проезд по ребру d займет 50 + t минут.
Предположим, что водители едут из вершины 1 в вершину 4, причем в единицу времени из 1 в 4 направляется одно и то же число водителей. В нашем примере оно равно 6. При этом, как легко показать, из 1 в 4 можно попасть по одному из двух маршрутов: 1-a-3-c-4 и 1-b-2-d-4. В нашей грубой модели водитель не будет тратить время на проезд через перекресток. Тогда время в пути для маршрутов будет определяться как сумма весов входящих в маршрут ребер. Например, для маршрута 1-a-3-c-4 время в пути составит fa + fc, а для маршрута 1-b-2-d-4 время в пути составит fb + fd. Обозначим через x транспортный поток на маршруте 1-a-3-c-4, а через y — транспортный поток на маршруте 1-b-2-d-4. Под транспортным потоком на маршруте подразумевается количество водителей, выезжающих из 1 в 4 по этому маршруту в единицу времени. При этом, очевидно, x + y = 6.
Легко показать, что для графа на рисунке 3,а поток на ребрах a и c равен x, а поток по ребрам b и d равен y. Соответственно, время в пути для маршрута 1-a-3-c-4 будет равно fa(x) + fc(x), а для маршрута 1-b-2-d-4 время в пути будет равно fb(y) + fd(y).
Водители, выбирая свой маршрут следования, ведут себя эгоистично. В нашем случае это значит, что они выбирают маршрут с наименьшими ожидаемыми издержками. Но чем больше водителей выбирают тот или иной маршрут, тем выше издержки на данном маршруте. С другой стороны, мы зафиксировали общее число машин, выезжающих из вершины 1 в вершину 4 в единицу времени, а значит, если каким-то маршрутом стало пользоваться большее количество автомобилистов, то есть какой-то маршрут, который стал использоваться меньше. Вероятно, что на этом втором маршруте издержки, напротив, упадут. Таким образом, первый, ранее привлекательный, маршрут становится более обременительным, а альтернативные маршруты при этом становятся более привлекательными. Это мотивирует водителей вновь изменить свой маршрут. Но такая «болтанка» происходит не всегда.
Введем понятие равновесия (Нэша–Вардропа). Назовем распределение потоков по маршрутам равновесным, если время проезда по всем используемым маршрутам одинаково и не превосходит времени в пути на неиспользуемых маршрутах.1
Смысл этого утверждения очень прост: равновесное распределение потоков по маршрутам — это когда водители так выбирают свои маршруты, что никому в отдельности не выгодно менять свой выбор. Если бы, например, для графа на рисунке 3,а реализовалось равновесие и мы бы рассмотрели произвольного водителя, использующего маршрут 1-b-2-d-4, то мы могли бы сказать, что этому водителю не выгодно менять свой маршрут.
Для нашего примера найти равновесие очень просто. Всего возможны три варианта:
1) x = 6, y = 0, fa(6) + fc(6) ≤ fb(0) + fd(0);
2) x = 0, y = 6, fa(0) + fc(0) ≥ fb(6) + fd(6);
3) x + y = 6, x > 0, y > 0, fa(x) + fc(x) = fb(y) + fd(y).
Заметим, что в нашем случае fa(t) + fc(t) =11t + 50 = fb(t) + fd(t). Отсюда имеем fa(0) + fc(0) = fb(0) + fd(0) = 50 и fa(6) + fc(6) = fb(6) + fd(6) = 116. Следовательно, варианты 1) и 2) отпадают. Для того чтобы найти равновесное распределение потоков, нужно решить систему уравнений 3):
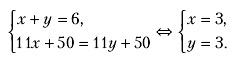
Легко доказать, что полученное решение удовлетворяет условиям равновесия. Действительно, время в пути на используемых маршрутах совпадает и равно 11·3 + 50 = 83 , а неиспользуемых маршрутов просто нет.
Резюмируя, техника поиска равновесий следующая.
- Все маршруты делятся на используемые и неиспользуемые в равновесии. Получается огромное количество вариантов разделений.
- Выбирается конкретное разделение.
- Ищется такое распределение суммарного потока по используемым маршрутам, чтобы время в пути на всех используемых маршрутах было одинаковым. Если такого не существует, разделение «бракуется». Если есть, переходим к следующему пункту.
- Проверяется, что для всех неиспользуемых маршрутов время в пути не ниже, чем на используемых.
Если найденное распределение потоков по маршрутам удовлетворяет этим условиям, то оно и есть искомое. Вообще говоря, равновесий может быть несколько или даже бесконечно много. Заметим также, что на практике, конечно, применяются намного более эффективные алгоритмы поиска равновесий. Описанный выше способ — самый примитивный, мы привели его из-за наглядности.
Пример выше иллюстрирует тот факт, что в равновесии ни один из водителей не может выиграть, изменив свой маршрут. Поэтому, если система находится в равновесии, то она в этом равновесии и останется (вообще говоря, мы должны были бы потребовать устойчивость равновесия, но сейчас не хотелось бы говорить об этом). Данное равновесие носит имя Нэша и Вардропа (об этом уже упоминалось чуть выше) по следующим причинам. Если рассмотреть игру, в которой водители являются игроками, маршруты — стратегиями (другими словами, возможными действиями игроков), а издержки, соответствующие маршрутам и взятые со знаком «минус», — выигрышами, то выписанное определение будет являться определением равновесия Нэша в построенной игре. Собственно, существование равновесия гарантируется теоремой Нэша, с которой можно познакомиться в любом учебнике по теории игр. В ней, в общем, и постулируется существование равновесия в играх, подобных рассмотренной нами. Вардроп же предложил два принципа, описывающих возможное поведение водителей. Первый из них предполагает, что все водители действуют оппортунистически и считают собственное влияние ничтожным. Второй принцип, напротив, говорит, что водители могут действовать согласованно с целью минимизировать общественные издержки. Собственно этими двумя принципами и их комбинациями, по мнению Вардропа, и описываются все возможные и существенные для анализа варианты поведения.
Парадокс Брайеса и неэффективные дороги
Немецкий математик Дитхард Брайес вошел в историю как автор простейшего примера, демонстрирующего, к чему приводит эгоистичное поведение.
Брайес рассмотрел простейшую транспортную сеть, соединяющую двумя непересекающимися маршрутами начальный и конечный пункты 1 и 4 (см. рис. 3).
Мы уже искали равновесие для графа на рисунке 3,а и получили, что x = y = 3,
fa(3) + fc(3) = fb(3) + fd(3) = 83.
Однако Брайес на этом не остановился и рассмотрел модификацию первоначальной сети, где построена дополнительная дорога, напрямую соединяющая промежуточные пункты (рис.3,б), которую мы назовем e. Дорога получилась приличного качества и относительно короткая, так что время проезда по ней определяется формулой
fe(t) = t + 10.
Заметим, что у водителей, которые едут из 1 в 4, появился новый маршрут 1-b-2-e-3-c-4. Каким будет новое равновесие и каким будет время проезда?
Можно себе представить, что в первое время, пока эта дорога еще мало кому известна, поток по ней равен 0 и, следовательно, у того водителя с нижнего маршрута, который первым свернул на нее, время проезда составит
fb(3) + fe(0) + fc(3) = 30 + 10 + 30 = 70.
Это явно меньше 83 минут. Ура, сворачиваем! Но что происходит дальше? За нами сворачивают новые машины, водители которых, видимо, провели те же самые расчеты! Та же самая логика, которая применялась и для исходной сети, должна быть применена и в этом случае — потоки перераспределятся так, что время проезда по каждому маршруту будет одинаково и никому из водителей не будет смысла менять маршрут. Мы получим новое равновесие.
Действуя по нашей схеме, мы должны определить возможные разделения маршрутов на используемые и неиспользуемые. Всего у нас будет 7 вариантов:
| 1-a-3-c-4 | 1-b-2-d-4 | 1-b-2-e-3-c-4 |
| + | 0 | 0 |
| 0 | + | 0 |
| 0 | 0 | + |
| + | + | 0 |
| + | 0 | + |
| 0 | + | + |
| + | + | + |
Пусть нам известно, что равновесие получается в случае, когда все маршруты используются. Обозначим через z транспортный поток на новом маршруте 1-b-2-e-3-c-4. Решим систему уравнений, которая получается из условия равновесия:
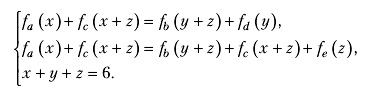
В первом уравнении мы написали, что времена проезда в равновесии для маршрутов 1-a-3-c-4 и 1-b-2-d-4 равны. Во втором уравнении мы записали то же требование для маршрутов 1-a-3-c-4 и 1-b-2-e-3-c-4.
Преобразуем систему, подставив вместо функций их значения:
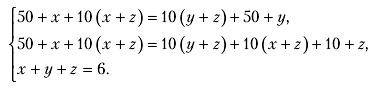
Решая систему, получаем x = 2,новые машины y = 2,новые машины z = 2, т. е. в равновесии суммарный поток распределится по маршрутам в равных долях x = y = z = 2, а время в пути для всех маршрутов составит
fa(2) + fc(4) = 50 + 2 + 40 = 92.
Замечание. То, что здесь и ранее в равновесии потоки по маршрутам оказались равны между собой, — чистая случайность и результат подбора таких функций весов, чтобы «получилось красиво». В равновесии у маршрутов равны времена в пути (!), а не потоки.
Что замечательно (с исследовательской точки зрения, с практической же точки зрения это ужасно), время в пути после добавления нового ребра для всех водителей возросло. Это увеличение является следствием того, что мы позволили каждому водителю поступать эгоистично, выбирая маршруты так, чтобы никому не было выгодно отклониться от равновесия.
Описанный выше парадокс Брайеса произрастает из неэффективности равновесия Нэша–Вардропа с точки зрения общественного блага. Говоря проще, из-за эгоистичности водителей суммарные издержки всех водителей в равновесии выше, чем вообще могли бы быть при некотором другом распределении.
Определим теперь понятие социального оптимума. Социальный оптимум — это такое распределение потоков по маршрутам, при котором суммарное время в пути у всех водителей минимально.
Тем самым, для того чтобы найти социальный оптимум в нашей системе, нам нужно было бы решить следующую задачу — найти
min (x·(fa(x) + fc(x + z)) + y·(fb(y + z) + fd(y)) + z·(fb(y + z) + fc(x + z) + fe(z)))
при условии x + y + z = 6, где x, y, z неотрицательны, т. е. найти
min (50·x + 11·x2 + 20·xz + 50·y + 11·y2 + 20·yz + 21·z2 + 10·z).
Выразив z, сводим задачу к поиску
min (816 – 92·x – 92·y + 2·xy + 12·x2 + 12·y2).
Можно доказать, что точкой минимума при условии неотрицательности переменных будет тройка (3, 3, 0).
Все описанные проблемы с пробками проистекают из-за того, что социальный оптимум обычно (как в нашем случае) не является равновесием.
Конечно, возможны ситуации, когда равновесие Нэша–Вардропа является социальным оптимумом, но в общем случае это не так.
Заметим, что в социальном оптимуме ребро e не используется. Оно неэффективно. Эгоизм же водителей приводит к его использованию. Можно показать, что это верно для любых неэффективных ребер (т. е. таких, от чьего удаления кто-то из водителей выигрывает, но никто не проигрывает). Их появление является следствием неэффективности равновесия.
Итак, мы показали, что из-за эгоизма водителей могут возникать неэффективные ребра и прочие проблемы. Невелика заслуга. Вопрос только в том, насколько (!) это плохо.
Чтобы ответить на него, нам нужно найти некоторую характеристику или численную меру эффективности распределения транспортных потоков при заданном графе и числе выезжающих автомобилей (в единицу времени). Первое, что приходит в голову, — совокупное время в пути.
Влияние эгоистичности водителей можно оценить по разнице между временем в пути в реализовавшемся распределении (т. е. равновесием) и временем в пути при оптимальном поведении водителей (т. е. социальном оптимуме). В нашем случае эта величина равна 92 – 83 = 9.
Много это или мало? Ответ зависит от графа и загрузок. Традиционно мерой неэффективности является так называемая «цена анархии» — отношение времени в пути в худшем равновесии ко времени в пути при оптимальном распределении потоков. В нашем случае «цена анархии» равна ![]() ≈ 1,1084.
≈ 1,1084.
Насколько большой может быть «цена анархии», зависит от того, какие функции весов мы выберем, и «не зависит» от размеров графа транспортной сети. Например, для нашей сети, в которой время в пути по ребру зависит от потока линейно, максимальное значение «цены анархии» равно 4/3.
Платные дороги
Замечательное свойство неэффективных ребер заключается в том, что с ними можно эффективно бороться. Действительно, достаточно запретить проезд по неэффективному ребру, как транспортная ситуация улучшится. Поставил кордон — и дело сделано!
В этот момент самое время вспомнить введение нашей статьи. Мы показали, что участники движения во многом сами являются причиной возникновения пробок. При этом разговоры о том, что нужно строить больше дорог для того, чтобы все поехало, не приведут ни к чему хорошему. Иногда, чтобы все поехало, надо дороги закрывать. Беспорядочное строительство, наоборот, может привести к ухудшению транспортной ситуации.
Только что мы сказали «поставил кордон — и дело сделано». Но ни один чиновник никогда не поставит кордон. Как же так: сначала за 29 миллиардов построим дорогу, а потом ее закрывать? Нонсенс! Уж лучше пусть смоет (как это произошло во Владивостоке в 2012 году). Тем более, ребро является неэффективным только при определенных загрузках. Возможно, ситуация и загрузка сети со временем изменятся и наличие ребра (ранее неэффективного) будет полезным. Было бы неприятно закрыть дорогу, дать ей разрушиться, а через десять лет строить на том же месте новую, так как она снова стала нужна.
Куда более прагматичным будет решение сделать проезд по неэффективным ребрам платным. С одной стороны, установив очень большую плату, мы можем свести поток по неэффективному ребру к минимуму. С другой стороны, мы позволяем планировщикам сохранить лицо. Дорога же работает и исправна — езжай на здоровье! Ну и наконец, если вдруг ситуация поменяется так, что ребро вновь станет эффективным, то плату можно будет снизить или вовсе убрать.
С точки зрения математики, это будет выглядеть так. Назначение платы за проезд по ребру е в размере α соответствует замене fe(x) на fe(x) + α. Это приводит, вообще говоря, к смещению равновесия. Правильное назначение платы делает возможным изменение равновесия в благоприятную сторону. Продемонстрируем это на примере.
Назначим плату за проезд по ребру e графа на рисунке 3,б в размере 6,5. Решая заново систему, мы получим, что новым равновесием будет точка ![]() . Издержки за проезд водителей снизились с 92 до 87,5. Отлично! Давайте увеличим плату в 1,5 раза до 9,75. Повторяя процедуру, найдем новое равновесие
. Издержки за проезд водителей снизились с 92 до 87,5. Отлично! Давайте увеличим плату в 1,5 раза до 9,75. Повторяя процедуру, найдем новое равновесие ![]() Издержки снова упадут до 85,25. Вспоминая, что минимальные издержки за проезд, которые вообще возможны (для этого графа и загрузок), составят 83, можно сказать, что мы уже совсем близки к цели. Действительно, лучшее, чего мы могли бы достигнуть, — это оптимальное распределение, поэтому в равновесии при введенных платах издержки не могут быть ниже 83. Когда мы дойдем до платы в 13, по ребру e водители ездить перестанут. При этом нам повезет, и новое равновесие будет социальным оптимумом (что наблюдается не всегда).
Издержки снова упадут до 85,25. Вспоминая, что минимальные издержки за проезд, которые вообще возможны (для этого графа и загрузок), составят 83, можно сказать, что мы уже совсем близки к цели. Действительно, лучшее, чего мы могли бы достигнуть, — это оптимальное распределение, поэтому в равновесии при введенных платах издержки не могут быть ниже 83. Когда мы дойдем до платы в 13, по ребру e водители ездить перестанут. При этом нам повезет, и новое равновесие будет социальным оптимумом (что наблюдается не всегда).
Но самое главное свойство платных дорог заключается в том, что, устанавливая подходящую плату, мы можем бороться не только с неэффективными ребрами, но и с возникающими пробками. Мы уже обсуждали выше, что пробки возникают из-за того, что нужно «выровнять» издержки за проезд по быстрым и медленным маршрутам, если быстрые маршруты не могут обслужить самостоятельно весь автомобильный поток. Этого требует принцип Вардропа. Но ведь плата за проезд тоже может выровнять эти издержки! Механика тут будет точно такой же, как в примере выше.
Теперь, когда мы знаем откуда берутся пробки и как можно их побороть, самое время отточить навыки.
Задачи
1. Найдите равновесное распределение потоков для транспортного графа на рисунке 3,б, если суммарно из 1 в 4 в единицу времени направляются 2 автомобиля.
2. Как можно объяснить следующее противоречие: в описанной в статье модели время в пути по дуге есть строго возрастающая функция от величины потока на дуге, а согласно фундаментальной диаграмме Гриншилдса эта зависимость не является однозначной — есть две ветки, одна из которых соответствует малым и умеренным плотностям и согласуется с отмеченной зависимостью, другая, соответствующая большим плотностям, приводит к убывающей зависимости времени в пути от величины потока?
3 (де Пальма). Из жилого района в рабочий район утром должны отправляться 10 000 автомобилей. Водитель каждого автомобиля хочет приехать ровно к 9 часам утра в рабочий район. При этом каждая минута опоздания штрафуется в 10 рублей, а каждая потерянная минута в пути или в ожидании начала рабочего дня, если водитель приехал раньше времени, стоит 3 рубля. Время в пути по свободной дороге занимает 60 минут. Но на середине дороги есть узкое место, пропускная способность которого ограничена 3000 автомобилей в час. Покажите, что равновесное распределение водителей по времени выезда из жилого района n(t) представимо в виде
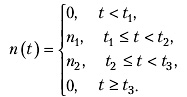
Найдите n1, n2 , t1, t2, t3.
4. Рассмотрите транспортный граф на рисунке 4. Считайте, что характеристики графов, включенных в оранжевые прямоугольники, совпадают с характеристикой транспортного графа на рисунке 3,б. Дороги, соединяющие вершины 1 и 6 с этими графами, такие, что по ним может проехать сколь угодно много автомобилей, причем время в пути будет пренебрежимо мало. Найдите равновесное распределение потоков, если суммарный поток из 1 в 4 равен: а) 2; б) 6; в) 10; г) 14.
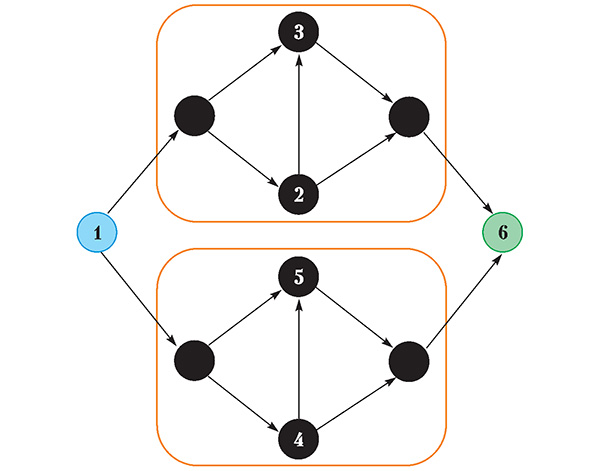
5. Являются ли дороги в графе на рисунке 4, соединяющие вершины 2 и 3, 4 и 5 соответственно, неэффективными, и если да, то при каком суммарном потоке?
1 Понятие равновесия было определено Джоном Нэшем (тем самым, о котором снят интересный фильм «Игры разума») в конце 40-х годов XX века. Концепция равновесия игры является центральной в теории игр, познакомиться с ней можно в любом учебнике по теории игр или исследованию операций. Позднее, в 1994 году, именно за эту концепцию Джон Нэш получил Нобелевскую премию по экономике. Мы также добавляем фамилию Дж. Г. Вардропа, которой чуть позже Нэша добавил к этой концепции условие «конкурентного рынка»: игрок, принимающий решение, пренебрегает тем, что его решение сколько-нибудь значительно поменяет ситуацию в транспортной системе (в нашей модели это и есть «рынок»). Когда игроков двое или трое (ситуации, рассматриваемые Нэшем), то очевидно, что так делать нельзя. Но когда игроков (водителей) десятки и сотни тысяч...
-
Только и знают одно - сделать платным.
А сделать АСУ для дорог по принципу демона Максвелла? Сейчас уже сотовые телефоны во всю выпускают с 4 ядрами, 3G или 4G, GPS. Почему бы не использовать такие внушительные вычислительные мощности для оптимизации движения? Создать систему, когда каждый водитель, начиная движение, сообщает пункт назначения, во время движения данные его машины постоянно используются для расчета оптимальных маршрутов. При чем сам смартфон используется для участия в распределенных вычислениях. Ну а определенные маршруты по ситуации могут блокироваться светофорами на развилках. Только светофоры должны быть особые, перед которыми нельзя стоять. Или, если разрешено, сворачиваешь на развилке, или едешь по другому пути.
Стимулировать можно тем, что для тех, кто будет участвовать в такой системе, меньше будут страховые сборы и транспортный налог.
Для тех, кто опасается угонов, можно делать такую комплектацию машины, что без начальной регистрации в такой системе автомобиль просто заводиться не будут.
P.S.Вот правда, меня сейчас поражает какие вычислительные мощности люди в карманах в холостую таскают.
Как говорится в появившейся шутке - "В твоем смартфоне больше вычислительных мощностей,чем у всего НАСА в 1969 году. НАСА запустило человека на Луну.Ты запускаешь птиц в свиней".
Надо разумно для социальной пользы их использовать.
P.S. Я уж не говорю о том, какую статистику подобная система позволит собрать, что позволит более осмысленно модернизировать старые дороги, и строить новые.
-
-
В прошлый раз введение платы за проезд обосновывалось еще и тем, что люди, видите ли, еще и начинают более интенсивно покупать машины и увеличивать перегрузку... Печень чувствует конкретную заказуху.
Но есть и способ противодействия этой подлянке: дело в том, что как бы не "задерживало" проезд строительство новой дороги, негативные обстоятельства некачественного исходного планирования могут быть в подавляющем числе случаев нейтрализованы строительством ЕЩЕ ОДНОЙ дороги, но уже с последовательным учетом всех факторов. Так вот: и учет этих факторов, и новая стройка должны осуществляться не за счет взимания с водителей платы за проезд, а за счет тех, кто произвел неграмотное исходное планирование и строительство первой трассы.
-
-
Формулы верные, выводы из них неверные. Что якобы надо сделать часть "неэффективных" дорог платными и все поедет. На самом деле, есть куча бесплатных для водителя альтернатив, которые воздействуют на равновесие и устранят влияние парадокса, даже если он проявится (в чем я сильно сомневаюсь, так как алгоритмы предсказания времени в пути сейчас далеки от совершенства, а парадокс предполагает идеальный навигатор):
- можно изыскать резервы пропускной способности на существующих дорогах, в текущей ситуации в Москве это можно сделать ВСЕГДА,
- можно изменять фазы светофоров
- можно даже воздействовать на прокладку маршрута яндекс-пробками и прочими навигаторами (не далее как вчера он мне сообщил что ехать 40 минут, вот только небольшая пробка перед переездом, и дальше все ОК:), ну да, постоял там те же 40 минут, а потом еще 40 минут действительно все ОК)
И вообще у нас пробки не из-за того, что не хватает пропускной способности прямых участков дорог, все дело в их пересечениях. Были бы идеально сделаны развязки (а в статье про них ни слова), чтобы никакие съезжающие/въезжающие не перекрывали основной ход трассы, вообще бы проблема не стояла. Тут еще и дисциплина важна, конечно, если в пять рядов направо поворачивать, никаких дорог не хватит.-
С реальным проявлением этого парадокса столкнулись в Германии. Согласитесь, немцы умеют дороги делать? Так постройка новой скоростной трассы привело к тому, что время проезда из А в Б реально увеличилось.
-
Наука должна уметь прогнозировать. Таким образом, учет сего обстоятельства, если он следует из конкретных предпосылок ДЕЙСТВИТЕЛЬНО "строго математически", должен производиться еще ПЕРЕД строительством автострады. А не учитываться путем взимания платы за проезд уже ПОТОМ. И единственный достойный выход из подобной ситуации - не взимание платы, а строительство ЕЩЕ ОДНОЙ дороги, но уже таким образом, когда строгий математический расчет показывает компенсацию негативных обстоятельств предыдущей стройки.
-
Вы же понимаете, что это нереалистично, так как потоки все время находятся в динамике. Но перекрывать дороги или делать их платными - тоже не выход.
-
Если эта наука не имеет предсказательной силы, а просто объясняет все постфактум, грош ей цена. Поясню: строительство новой дороги в указанном негативном случае имело отрицательные последствия именно в среднем - а среднее можно просчитать, как функциональный интеграл по частным траекториям (в данном случае - всевозможным весовым соотношениям графов). Соответственно, есть варианты дорожного строительства (построения графов по выбранным узловым точкам перекрестков), которые дадут средний выигрыш, а не потерю. И из средней по миру пользы от строительства новых дорог можно сделать вывод, что даже в самом приблизительном выборе вероятность избрать положительный вариант значительно больше, чем отрицательный, последнее - исключение из правила.
Это касаемо среднего исхода. а касаемо частной динамики... Дело в том, что ДАЖЕ ЕСЛИ законодательно удастся наладить плавающий трафик за проезд (а не фиксированные, раз и навсегда, расценки - тогда возвращаемся к преимущественному среднему, которое, как я уже указал, разрешается иначе), вопрос остается в системе оповещения водителей о значении новых расценок, влияющих на "вес" графа. Но раз так - то по ЭТОЙ ЖЕ системе гораздо логичнее просто рассылать всем водителям "вес" по банальной загруженности трассы в режиме реального времени с указанием оптимального на данный момент маршрута и скоростной стратегии поведения (так как цена все равно будет рассчитываться из этих параметров). Чуете? Необходимость платы в динамике ТЕМ БОЛЕЕ пропадает, так как все сводится к вопросу совершенства системы слежения, оповещения и регулировки. А как уже указывалось выше в дискуссии, нынешние системы, призванные решать эту проблему, страдают немалыми недостатками... Если по ним еще и цену назначать - и по ним же пытаться перенаправить водителей, то жопа (простите за самый точный, хоть и грубоватый термин) будет полная...-
Вы упускаете один очень важный момент. Эгоистов. Можно маршруты рассылать, да только всегда найдутся умники, которые сообразят, что если рекомендациям не следовать, то очень даже выигрыш можно получить в сравнении с "лохами". И число таких растет все больше и больше, пока вот это равновесие Нэша и не наступает.
Есть система, которая в совокупности оптимальна по всем участникам игры. Но это не состояние устойчивого равновесия. Отдельным игрокам становится оооочень выгодно играть не по правилам.А где один, там и два,и толпа. И вот Вам и 90-е годы. И в целом получается всеобщие заторы.-
Эгоисту выгодно быстрее проехать из пункта "А" в пункт "В". И хрен он проедет по затору. Т. о. этот параметр просто должен быть одним из определяющих общую стратегию в расчете. Не обязательно следовать общему "социальному оптимуму" с глобальным минимумом, обеспечивающим, однако, простой одиночек. Многокомпонентные задачи изобилуют массой локальных минимумов, которые обеспечивают хоть и больший средний простой, но однако же значительно ближе к оптимуму, чем "слепой вариант" (тем более обеспечивающий глухую пробку).
-
Подождите. Вы предлагали делать рассылки рекомендуемых маршрутов. По ним можно поехать, но по их весу это означает, что затрачиваемое время будет больше. Эгоист исходит из того, что большая часть последует по более долгому маршруту, тем самым позволив ему проскочить по быстрому без проблем. Это же как в финансовой пирамиде. Первые снимают куш, все последовавшие за ними - теряют. Малая часть выиграла сильно. Суммарно по всем выигрыш меньше, чем если бы эгоистов не было.
-
-
-
...и, кстати, еще один момент. Я, забив нафиг на все программы и навороченные девайсы, выезжаю поутру на работу по привычной дороге. И вдруг обнаруживаю, что за проезд по ней уже НАДО ПЛАТИТЬ... Что я делаю? Поворачиваю! И ищу другой путь (разумеется, не всегда, но в НЕМАЛОМ числе случаев). Время на перестроение, задерживающее другие машины. Движение к новому пути по дополнительному графу (с неизбежным вкладом в увеличение трафика) и так далее... Каков ТЕПЕРЬ результат моих эгоистических действий скупердяя в сумме по всем, мне подобным?
-
Вы повернете, другие нет. В этом и смысл платных дорог.
И потом, платными предполагается делать только новые дороги. В этом и парадокс. Реальный. Строительство новой дороги приводит к тому, что в целом добираться становится сложнее.
И потом. Эгоист не значит жадина. Эгоист очень даже много может тратить на себя любимого.-
Заметьте: обо всех я и не говорил (и даже себя упомянул, как поворачивающего НЕ ВСЕГДА) - причем намеренно. Я говорил о значительной части, которая, несомненно, повлияет на трафик. Насчет только новых дорог - с одной стороны, это не уменьшит упомянутую сложность, а динамически изменяющаяся система оплаты лишь усложнит ориентацию в ситуации, превратив все в сущий кавардак. С другой... Вы знаете аппетиты наших "бизнесменов" и властей. Неужели Вы всерьез уверены в том, что система, будучи единожды введенной, не будет распространена на все дороги?)) Под тем тезисом, что "Регулировать ценами движение только на одной дороге малоэффективно, а система и так уже переусложнена, так что несколько терминалов до кучи не ухудшат ситуацию с оплатой". И уж будте уверены - драть за проезд будут не "по науке", а сообразно личному их эгоизму, в данном случае полностью альтернативному самой банальной жадности. И в этом случае вся внешняя рациональность предоставленных расчетов тем более полетит в одно теплое и темное место.
Кстати, из личных наблюдений: пробки в подавляющем большинстве случаев - результат вынужденного торможения у дорожных препятствий, как-то: выбоины на дороге, железнодорожные переезды по рельсам, перекрестки, аварии и т. д. Без них даже в условиях плотного потока машин пробки практически не возникают. Так что лучший способ борьбы с пробками - ремонт дорог, строительство удобных развязок вместо стандартных (пусть и значительно более компактных и дешевых) перекрестков, строительство подземных и надземных пешеходных переходов, быстрый и своевременный попавших в аварию машин и т. д.
-
-
-
-
-
-
-
-
-
Извините за резкость предыдущего письма.
Я бы принял расположение ребра е из вершины 2 в вершину 3, если бы хотя бы один автомобиль имел начальный пункт в вершине 2, а конечный - в вершине 3. Но в примере нет таких автомобилей, поэтому логичнее было бы расположить ребро е параллельно имевшимся ребрам или сразу от 1 до 4. Из-за этого обесцениваются дальнейшие рассуждения о "неэффективных ребрах-дорогах".
-
У меня выходит 0, 0, 2, так как время проезда по пути 1-b-2-e-3-c-4 двух автомобилей выходит равно 52 и это даже меньше, чем проезд 1 авто по 1-a-3-c-4 и 1-b-2-d-4 (равное 62 и там и там)














