Сохранение импульса, уравнение Мещерского и банджи-джампинг

А. Рыбаков
«Квант» №3, 2012

Очень редко появляются совсем новые сюжеты задач механики. Но сейчас такое произошло. Движение прыгуна в экстремальном аттракционе банджи-джампинг обладает некоторыми удивительными особенностями, которые требуют объяснения. Оказалось, что это можно сделать, если применить к прыгуну и привязанному к нему канату уравнение, выведенное нашим соотечественником еще в позапрошлом веке.

Экстремальный аттракцион

В телевизионных репортажах из дальних стран уже неоднократно рассказывалось о таком экстремальном развлечении: к ногам человека привязывают свободной конец упругого каната, другой конец которого закрепляют, после чего человека сталкивают с большой высоты (рис. 1). Это и есть банджи-джампинг. Много ссылок на этот аттракцион дает Интернет, попал он уже и в Википедию. Будем для простоты называть его просто джампингом. В этом прыжке много разных фаз, и, соответственно, много удовольствий поджидает прыгуна. Но нас сейчас интересует только одно обстоятельство — видеосъемка показала, что человек летит вниз с ускорением, превышающим ускорение свободного падения g. На первый взгляд, это представляется удивительным — ведь, казалось бы, прыгун и часть каната ускоряются только силой тяжести, никаких других сил обнаружить не удается.

Рис. 1.

Однако начнем с самого начала. Выясним, к какому типу систем можно отнести прыгуна с канатом и какие законы (уравнения) надо использовать для описания динамики такой системы.

Прыгун и движущаяся часть каната — это типичный пример тела с переменной массой. Во избежание недоразумений надо сказать, что речь идет об изменении массы тела за счет отсоединения какой-то его части (или присоединения извне). В нашем случае при движении непрерывно увеличивается покоящаяся часть каната и, соответственно, уменьшается масса движущейся его части. Это очевидное обстоятельство и окажется важнейшим для наших дальнейших рассуждений.

Поставим самые напрашивающиеся вопросы. Что происходит с импульсом системы? Что происходит с ее механической энергией? Как записывается основное уравнение динамики для такой системы?

Попытаемся ответить на все эти вопросы. Но прежде рассмотрим совсем простой, но очень важный для наших рассуждений пример.

Щелканье кнута и закон сохранения импульса

В раннем-раннем детстве я видел в дачном поселке под Ленинградом, как местные жители встречали вечером стадо коров (позднее коров в дачной местности уже не было). Подгоняя буренок, пастух щелкал кнутом. Вот оно!

Молодому читателю, возможно, надо напомнить, как устроен кнут. А устроен он очень просто: к палке (рукоятке, кнутовищу) привязан узкий длинный ремень (иногда — веревка). Это «устройство» называют еще бичом. Так, в известном стихотворении Н. А. Некрасова эти слова стоят рядом:

Там били женщину кнутом,
Крестьянку молодую.
Ни звука из ее груди,
Лишь бич свистал, играя...

Двинув кнутовище, пастух сообщает всему ремню импульс — а дальше начинается самое для нас интересное. Конец ремня, привязанный к остановившемуся кнутовищу, тормозится, и всё меньшая часть ремня продолжает движение (рис. 2). Но в точке перегиба никакая сила на движущуюся часть ремня не действует, значит, ее импульс не изменяется. А поскольку масса этой части ремня уменьшается, то скорость ее должна увеличиваться. Таким образом, движущаяся часть ремня непрерывно ускоряется. По-видимому, конец ремня даже переходит через скорость звука — и раздается характерный очень громкий щелчок.

Рис. 2.

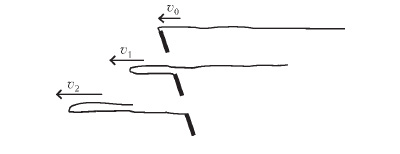
Человек, привыкший к рассуждениям, основанным на втором законе Ньютона, может спросить: «Какая же сила ускоряет часть кнута?» В том-то и дело, что никакие внешние силы к ускорению части кнута не имеют отношения. А движущаяся часть ремня непрерывно ускоряется потому, что этого требует закон сохранения импульса. Аналогия с движением каната в джампинге совершенно очевидна. Привяжите к концу ремня какое-нибудь тело — аналогия станет еще нагляднее. Но в джампинге в дело вмешивается еще и сила тяжести. Значит, в общем случае нам надо иметь уравнение, описывающее движение тела переменной массы под действием внешних сил. В одном крайнем случае (в отсутствие внешних сил) уравнение должно обеспечивать сохранение импульса, как в случае с кнутом, в другом (при неизменной массе) — переходить в обычный второй закон Ньютона.

Порядок в этом вопросе навел еще в позапрошлом веке российский ученый Иван Всеволодович Мещерский.

Уравнение Мещерского

Иван Всеволодович Мещерский родился в Архангельске в 1859 году. С 1878 по 1882 год он учился на математическом отделении физико-математического факультета Петербургского университета. После окончания был оставлен в университете для подготовки к профессорскому званию. Первые результаты по интересующей нас теме относятся к 1893 году. В 1897 году Мещерский защищает магистерскую диссертацию на тему «Динамика точки переменной массы». Некоторые дополнительные результаты были опубликованы в 1904 году в работе «Уравнения движения точки переменной массы в общем случае». Эти работы были включены в книгу И. В. Мещерского «Работы по механике тел переменной массы», изданную в 1949 году в серии «Классики естествознания». Именно это издание есть в моей личной библиотеке. (Несколько раз я приносил эту книгу в класс, чтобы показать ученикам, как удручающе громоздки уравнения механики, если они записаны без использования векторных обозначений.)

Мещерский оставил след не только как ученый, но и как выдающийся педагог высшей школы. С 1902 года до конца своих дней он возглавлял кафедру теоретической механики в Петербургском политехническом институте. Удивительна судьба выпущенного в 1914 году «Сборника задач по теоретической механике», составленного группой преподавателей под руководством И. В. Мещерского. У меня на полке стоит 33-е издание этого задачника, увидевшее свет в 1973 году, т. е. менее чем за 60 лет книга выдержала 33 издания! Другого такого примера я не знаю. А ведь в 1973 году история задачника отнюдь не закончилась. Многие сюжеты, которые нам сейчас известны по школьным и вузовским задачникам, впервые появились именно в этой книге.

Теперь — об уравнении Мещерского. Кратко напомним основополагающие моменты. Согласно Мещерскому, основной закон динамики тела переменной массы записывается в виде

    (*)

где  — сумма всех внешних сил, действующих на тело, M (t) — зависящая от времени масса тела,  — скорость изменения этой массы,  — относительная скорость отсоединяемого вещества (т. е. скорость отсоединяемых частей относительно «материнского» тела). Если речь идет именно об уменьшении массы, то, конечно,  < 0. Главный (для всех учебников) пример применения уравнения (*) — это анализ движения ракеты, в этом случае u — скорость истечения продуктов сгорания топлива, || — массовый расход топлива. В русскоязычной литературе уравнение (*) называют уравнением Мещерского. Оно является следствием фундаментального закона изменения импульса для системы материальных точек. Поэтому, в частности, некоторые задачи на интересующую нас тему были решены до работ Мещерского без использования уравнения (*). Можно переписать уравнение Мещерского еще в таком «почти симметричном» виде:

где производные по времени обозначены соответствующими буквами со штрихами.

Уравнение (*) является обобщением второго закона Ньютона — к известным нам членам добавляется еще одно слагаемое. Конечно, все члены имеют размерность силы, и возникает соблазн назвать новое слагаемое тоже какой-нибудь силой. Так обычно и поступают авторы, пишущие об уравнении Мещерского. Они называют новое слагаемое «реактивной силой». Необходимость введения такой терминологии представляется весьма сомнительной. Эти авторы просто хотят сохранить возможность говорить, что тело (даже тело переменной массы) ускоряется какой-то силой. Но это не так! И мы это уже видели на примере кнута (и еще увидим ниже — в последнем разделе статьи).

В общем случае, конечно, уравнение Мещерского является, как и второй закон Ньютона, дифференциальным уравнением второго порядка относительно функции . Ограничиваясь в школьном курсе постоянными силами (и, соответственно, равноускоренным движением), мы как бы не замечаем этих математических проблем. Но с уравнением Мещерского так поступать не удается, кроме редчайших исключений. Практически любая содержательная задача о движении тела переменной массы приводит к дифференциальному уравнению.

Задача Кейли

На одном достаточно простом примере покажем, как записывается уравнение Мещерского для конкретного движения объекта интересующего нас типа и как можно, не гонясь за математической строгостью, найти его решение. Читатели, интересующиеся лишь основной линией наших рассуждений (о джампинге), вполне могут пропустить этот раздел.

Рис. 3.

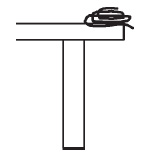
В своей диссертации в обзоре литературы Мещерский пишет: «Изменение массы, совершающееся непрерывно, рассматривает впервые, насколько мне известно, Кейли». И действительно, английский математик Артур Кейли в 1857 году опубликовал статью, в которой проанализировал следующую задачу:

Тяжелая цепь свернута в клубок на самом краю стола (рис. 3), а одно звено свешивается за край стола. Как будет двигаться конец цепи, предоставленной самой себе?

Кейли, конечно, не знал уравнения Мещерского. Мы же воспользуемся этим уравнением. Будем отсчитывать вертикальную координату конца цепи х вниз от края стола. Запишем уравнение (*) для движущегося участка цепи длиной х. Пусть масса единицы длины цепи равна ρ. Тогда движущийся участок имеет массу m = ρx, на него действует сила тяжести ρgx, за единицу времени масса этого участка увеличивается на . Скорость элемента цепи, лежащего на столе, относительно движущегося участка цепи равна . Так что уравнение (*) в проекции на ось х примет вид

и мы получим следующее уравнение для функции х(t):

xx'' = xg – x' ².

Это, как уже сказано, и есть дифференциальное уравнение второго порядка (звучит пугающе). Математики умеют решать такие уравнения, выполняя формальные преобразования, придумывая замены переменных и тому подобное. Но мы же физики — мы пойдем своим путем.

Подумаем: какого типа движение может совершать свешивающийся участок цепи? О равномерном не может быть и речи. Может быть — равноускоренное? Что ж, попробуем.

Предположим, что свешивающийся со стола участок цепи движется с неким неизвестным нам пока постоянным ускорением a (a < g). Это предположение может показаться слишком смелым, но ведь мы ничем не рискуем — если оно неправильно, мы придем к противоречию и тогда будем придумывать что-нибудь другое. Итак, пусть

х'' = a = const.

Тогда

х' = at , .

Подставим эти соотношения в наше дифференциальное уравнение и после совсем простых алгебраических преобразований получим

Таким образом, наше предположение блестяще подтвердилось — конец цепи движется с постоянным ускорением, и мы решили задачу Кейли. Если математик выразит неудовольствие, увидев такое «решение», заметим, что физик имеет право добывать информацию любым способом.

Почему же сила тяжести сообщает нашей цепи ускорение, меньшее g? На очень наивном языке можно было бы ответить, что часть силы тяжести тратится на приведение в движение покоящихся до этого элементов цепи.

А теперь попробуйте догадаться, как будет двигаться цепь (или канат) под действием силы тяжести, если, наоборот, элементы цепи останавливаются.

Складываемый коврик

Что происходит с механической энергией при движении по канату (или какому-то другому представителю гибкой связи) «точки перегиба»? На первый взгляд, кажется, что канат можно считать идеальным в том смысле, что при таком движении потери механической энергии не происходит. Но это не так! Рассмотрим столь простое движение интересующего нас объекта, что уравнение Мещерского сведется к алгебраическому уравнению (обсуждаемая задача есть, например, в книге П. Гнэдига, Д. Хоньека и К. Райли «Двести интригующих физических задач»; вып. 90 Библиотечки «Квант»):

Узкий длинный ковер (ковровая дорожка) лежит на полу (рис. 4). Конец ковра загибают и тянут назад со скоростью . Масса единицы длины ковра равна ρ. Какую силу F прикладывают к концу ковра?

Рис. 4.

Когда конец ковра, к которому приложена сила, пройдет путь L, точка перегиба ковра пройдет путь L/2, т. е. она движется не со скоростью , а со скоростью w = /2. За время ∆t в движение вовлекается участок ковра длиной ∆l = w∆t и массой ∆m = ρw∆t. Поэтому уравнение Мещерского принимает совсем простой вид:

Нам известны все параметры, описывающие движение ковра. Рассмотрим разные члены в балансе энергии в тот момент, когда ковер сложен вдвое. К этому моменту точка приложения внешней силы F пройдет, как уже сказано, путь L. Значит, этой силой будет совершена работа

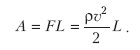
Теперь сосчитаем кинетическую энергию движущейся части (т. е. половины) ковра:

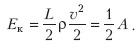
Мы получили, что ровно половина работы внешней силы потеряна. Такой вот удивительный результат! И нам надо запомнить на будущее, что массивные гибкие связи нельзя считать идеальными — при движении точки перегиба мы обязательно теряем заметную часть механической энергии. Но, подчеркнем, речь идет именно о массивных связях — к «невесомым» нитям, связывающим грузы в наших школьных задачах, всё это отношения не имеет.

(Читатель может вспомнить, что удивительная «двойка» в балансе энергии появляется в курсе физики в самых неожиданных местах: при зарядке конденсатора, при поднятии жидкости в капилляре и т. п.)

Возвращение к джампингу

Мы подробно обсудили разные аспекты проблемы, теперь у нас всё готово, чтобы написать уравнение Мещерского для «участников» джампинга — движущейся части каната и прыгуна. Направим ось х вниз и спроектируем уравнение Мещерского на эту ось. Будем аккуратны со знаками: вектор относительной скорости останавливающейся части системы направлен вверх, поэтому u = –. В задаче о ковре мы уже выяснили, что за единицу времени останавливается часть каната массой ρ/2 , поэтому уравнение примет вид

(здесь M — масса движущейся части каната и самого прыгуна, t — время полета, ρ — как и выше, линейная плотность каната), или

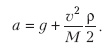
Это, конечно, не решение задачи, ведь М и  — неизвестные нам пока функции времени. Но ясно, что скорость со временем растет, а масса М — падает. Таким образом, мы доказали, что ускорение прыгуна в любой момент времени t > 0 больше ускорения свободного падения g и растет со временем. Качественно картина явления представляется нам вполне ясной: тело с уменьшающейся массой приобретает под действием силы тяжести всё больший импульс, а значит — ускоряется. И этот эффект будет тем сильнее, чем больше масса каната (по сравнению с массой прыгуна).

Новый опыт

Снова вернемся к понятию реактивной силы. В элементарных курсах физики реактивную силу, приводящую в движение ракету, обычно объясняют как силу давления продуктов сгорания топлива на стенку камеры сгорания. Представляется, что иногда такое «объяснение» может затемнять суть дела.

Рассмотрим совсем простой, «школьный» опыт. В кузов игрушечного автомобиля поместим длинную тяжелую ленту. Она должна быть свернута таким образом, чтобы иметь возможность разматываться и покидать кузов с минимальным трением. Закрепим конец ленты на демонстрационном столе и толкнем автомобиль. Лента, покидая кузов и останавливаясь, не уносит импульс, и, следовательно, импульс автомобиля с остатком ленты не меняется. Но масса-то уменьшается! Значит, скорость должна увеличиваться. Итак, лента разматывается — и автомобильчик разгоняется!

Ясно, что никакой реактивной силы, толкающей автомобильчик вперед, обнаружить не удается (нет никакого давления на стенку кузова). «Но это то же самое, что кнут!» — может сказать читатель. Ну да! Тем удивительнее, что никакого упоминания о таком опыте я никогда не видел. Удастся ли реально продемонстрировать этот опыт, зависит от того, сможет ли экспериментатор уменьшить силу трения — с одной стороны, между автомобилем и столом и, с другой стороны, между лентой и кузовом — до необходимых значений. Указание экспериментатору: при сматывании ленты не должна меняться ее высота над столом, а автомобильчик должен быть легким (по сравнению с лентой).

Автору было бы очень интересно услышать об успехах в проведении этого опыта.