Звездная величина объекта определяется как логарифм (по основанию 10) отношения его яркости (регистрируемого потока энергии за единицу времени на определенной длине волны) к яркости звезды Вега L₀ с некоторым коэффициентом. Даны графики зависимости наблюдаемой звездной величины от времени для 12 цефеид из галактики M100. Вычислите примерное расстояние до этой галактики.

В геометрии Лобачевского не выполняется пятый постулат Евклида, аксиома параллельных. Вместо него принимается, что существует бесконечно много прямых, проходящих через не лежащую на прямой l точку и не пересекающих l. Геометрию Лобачевского можно реализовать на обычной евклидовой плоскости (модель Пуанкаре в круге) или на специальной поверхности в трехмерном пространстве — псевдосфере. Прямыми Лобачевского на этой поверхности являются геодезические, то есть линии кратчайшей длины, соединяющие две точки. Как выполнить явное построение псевдосферы на основе модели Пуанкаре в круге? Другими словами, как склеить псевдосферу из одной или нескольких областей плоскости Лобачевского?

Далекие предки человека были, скорее всего, темнокожими. Судя по генетическим данным, кожа была темной и у общих предков Homo sapiens, когда около 70 000 лет назад они вышли из Африки и начали расселяться по Евразии. Но позднее во многих популяциях Homo sapiens кожа сильно посветлела. Теперь очень темная кожа свойственна, за немногими исключениями, лишь населению тропических широт и выходцам из тропических регионов. Народы, давно живущие в умеренных широтах, всегда в той или иной степени светлокожие. Как вы думаете, с чем это может быть связано?

Даны арабские глаголы в форме второго лица единственного числа настоящего времени мужского рода изъявительного наклонения (‘ты вращаешься (м.р.)’) и в двух формах второго лица единственного числа повелительного наклонения: мужского рода (‘вращайся (м.р.)!’) и женского рода (‘вращайся (ж.р.)!’), записанные в латинской транскрипции. Некоторые формы пропущены: <...>. Заполните пропуски. Поясните ваше решение.

В деревне живет 200 человек. Все они делятся на грибников и домоседов. Грибники каждый день ходят в лес за грибами, а домоседы проводят время в деревне. Домосед может в течение дня заметить каждого грибника с вероятностью 0,1%, а грибник в течение дня может заметить другого грибника с вероятностью 0,9%. Если домосед заметит грибника, то на следующий день сам станет грибником, а если грибник заметит другого грибника, то на следующий день станет домоседом. Оцените, сколько будет грибников к концу лета, если в начале лета их было двое.

Во время круиза на теплоходе Петра заинтересовал такой вопрос: есть ли среди 200 пассажиров кто-нибудь, то родился с ним в один день (годы рождения могут отличаться)? Ответы на свои вопросы он привык получать, подбрасывая монетку. Какая вероятность больше — что Петр встретит на теплоходе такого пассажира или что выпадет орел (то есть 1/2)?

Одежда очень плохо сохраняется в захоронениях, и прямых данных о времени ее возникновения мало. Тем не менее антропологи, археологи и биологи, пользуясь косвенными данными, выдвигают гипотезы о том, когда люди начали изготавливать и носить одежду. Как вы думаете, какие данные используют ученые, чтобы это установить?

Расшифруйте при помощи данного ключа такую депешу: «региона — экспедиция — видят — современных — данными — начала — войны — участии — этого — решили — двух — числа — современного — мировой — региона — с — данными». Сколько вариантов шифровки приказа «Огонь» можно составить для данного ключа?

У Васи и Пети есть три бесконечных набора цветных шариков: синие, маленькие красные, большие красные. Шарики в каждом наборе пронумерованы натуральными числами по возрастанию размера. Вася говорит, сколько ходов будет идти игра. Каждым ходом Вася выбирает один из шариков, а Петя должен подобрать к нему пару другого цвета. Если в конце игры после упорядочивания пар по размеру красных шариков окажется, что синие шарики тоже идут в порядке возрастания размера, то Петя выиграет. Иначе выигрывает Вася. Кто победит при оптимальной игре? А если наборы нумеруются целыми числами?

Один из этапов получения генно-модифицированных микроорганизмов — отбор (селекция) клеток, успешно встроивших в свой геном определенный набор генов. Для этого используют «маркерные» гены. «Прямая» селекция — когда мы отбираем только те клетки, в которых работает определенный ген. Но иногда необходимо провести и «обратную» селекцию — отобрать те клетки, в которых нет заданного гена или заданный ген не работает. Каков может быть принцип обратной селекции? Какие функции могут выполнять белки, закодированные маркерными генами для обратной селекции? Что должен делать белок, закодированный геном-маркером, который годится и для прямой, и для обратной селекции?

Известно, что древние египтяне пользовались словесно-слоговым письмом. Знаки древнеегипетского письма получили названия «иероглифы» (в переводе с греческого ‘священные высеченные знаки’). Один иероглиф мог передавать отдельный слог или целое слово. Ниже приводятся древнеегипетские имена в иероглифической записи с их условным чтением и принятыми русскими соответствиями: <...>. 1. Прочтите имя фараона. 2. Запишите имя фараона Менхепер-Ра.

Фигура F состоит из четырех склеенных между собой квадратиков, в которых имеются выступы и пазы. а) Обложите фигуру F копиями этой же фигуры в один слой. б) Обложите фигуру F копиями этой же фигуры в два слоя. в) Докажите, что копиями фигуры F нельзя покрыть плоскость без пробелов и наложений.

Вспомните, как вы в детстве качались на качелях. Сначала вы просто сидели на качелях и вас кто-то раскачивал, а потом вы научились раскачиваться сами. Когда качели кто-то качает, физический механизм ясен. А когда вы сами качаетесь стоя, вы периодически приседаете, и сила толчков прикладывается в направлении, перпендикулярном направлению движения качелей! Почему же при этом качели раскачиваются?

Анализ химического состава перьев случайно пойманной птицы на Новой Гвинее показал, что в перьях содержится яд, идентичный яду лягушек-древолазов из Южной Америки. У других животных этот яд обнаружен не был. 1. Как (кроме случайной конвергенции) можно объяснить наличие идентичного яда у таких далеких родственников, как лягушки и птицы? 2. Какие выгоды, кроме защиты от хищников, может давать птицам ядовитость?

При расшифровке аудиозаписей иногда какие-то их отрезки оказываются поврежденными и отдельные звуки не получается точно разобрать. В этом случае определить, какой именно звук был произнесен, может помочь знание того, как устроен язык. Восстановите поврежденные участки аудиозаписи по тому, какие звуки были произнесены до или после утраченных фрагментов.

Будем рассматривать суммы дробей, у которых в числителях стоят единицы, а в знаменателях — последовательные натуральные числа от 2 до n. Найдётся ли такое n, что сумма дробей окажется целым числом?

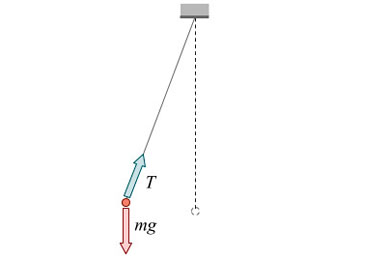
Рассмотрим очень длинный маятник, у которого точечный грузик находится в лаборатории на уровне земли, а точка подвеса унесена далеко в космос, хотя по-прежнему считается жестко связанной с Землей. Вращением Земли пренебрежем. Вычислите период малых колебаний такого математического маятника. Какой еще известный вам процесс имеет тот же период?

У некоторых живородящих видов клещей самка, паразитирующая на яйце насекомого, рождает от 5–6 до нескольких десятков самок и только одного самца. Родившись, самец не питается, ни с кем не спаривается и через несколько часов погибает. Зачем нужен этот самец и почему он всегда один?

Даны арифметические примеры на языке северный паме (все числа не превышают 30): (1) rnuɁ × rnuɁ = kara tenhiuɲ santa. (2) kara tenhiuɲ nuji + kara tenhiuɲ nuji = kanuje tenhiuɲ giriu. (3) kara tenhiuɲ teriuhiɲ? + santa = kanuje tenhiuɲ. (4) kanuje tenhiuɲ gitʃ’ai + gitʃ’ai = karnuɁ tenhiuɲ nuji. (5) kanuje tenhiuɲ rnuɁ + kara tenhiuɲ rnuɁ = karnuɁ tenhiuɲ teria. (6) kara tenhiuɲ giriu + kanuje tenhiuɲ santa = karnuɁ tenhiuɲ gitʃ’ai. Запишите пример (6) цифрами. Запишите на языке северный паме: 2, 13, 22, 24, 31.

Даны окружность с центром О и точка А вне окружности. а) Проведен диаметр окружности. Пользуясь только линейкой, опустите перпендикуляр из точки А на этот диаметр. б) Через точку А проведена прямая, не имеющая общих точек с окружностью. Пользуясь только линейкой, опустите перпендикуляр из точки О на эту прямую.