Бегущий по волнам

В первой задаче можно рассмотреть два предельных случая, в которых выражения для скорости волн уже известны. Пи-теорема, по сути, говорит о том, что есть некоторая функция, которая эти два предельных случая связывает в одну модель.

Воспользуйтесь результатом первой задачи, а также подумайте о том, в каком направлении распространяются эти кильватерные волны (см. задачу Что общего у утки и авианосца?).

Сначала разберемся с первой задачей. Нужно определиться, какие переменные здесь важны. Сразу ясно, что в их число входят ускорение свободного падения \(g\), длина волны \(\lambda\) и глубина воды \(h\). Еще нам, конечно же, интересна скорость распространения волны (фазовая скорость) \(v\). Нетрудно проверить, что из этих четырех переменных можно составить лишь две независимые безразмерные величины. Первая — совсем тривиальна: \(\pi_1 = h/\lambda\). Вторую можно найти с помощью анализа размерностей: \(\pi_2 = v / \sqrt{g\lambda}\).

Следуя пи-теореме, эти величины можно связать при помощи некоторой функции: \(F(\pi_1, \pi_2) = 0\). Если думать о величинах \(\pi_1\) и \(\pi_2\) как об осях абсцисс и ординат (то есть как об условных \(x\) и \(y\)), то решение этого уравнения задает некоторую кривую (это и есть связь между \(x\) и \(y\)) на координатной плоскости, вдоль которой значение функции \(F\) равно нулю. Тогда это же уравнение можно переписать, выразив одну переменную через другую: \(\pi_2 = f(\pi_1)\), где \(f\) — некоторая другая неизвестная функция (см. Теорема о неявной функции).

Подставим значения наших безразмерных величин:

Фактически, мы получили выражение для скорости волн воды при произвольных значениях глубины и длины волны. Функция \(f\) нам по-прежнему неизвестна, но ее примерный вид можно угадать, рассмотрев два предельных случая. Когда глубина много меньше длины волны, то очевидно, что от длины волны ничего зависеть не должно, и тогда \(f(h/\lambda) = \sqrt{h / \lambda}\), а тогда фазовая скорость будет равна \(v = \sqrt{g h}\). В обратном случае, когда \(\lambda \ll h\), от глубины ничего не зависит, и, стало быть, \(f(h/\lambda) = 1\) (или другой константе), и \(v = \sqrt{g\lambda}\).

Получается, что \(f(x)\) — это функция, которая ведет себя как \(\sqrt{x}\) при малых значениях \(x\), и асимптотически приближается к 1, при больших \(x\). Нарисуем график зависимости скорости \(v\) от глубины \(h\) (рис. 2).

Здесь важно сделать оговорку. Функция \(f(x)\) определяется с точностью до некоторого коэффициента. Это значит, что при \(x\gg 1\) \(f(x)\) вполне может быть равно и 2, и 10. Этот коэффициент можно отыскать, точно решив задачу с помощью уравнений гидродинамики, но в анализе размерностей вполне разумно предположить, что эта константа равна 1. Отличия этого коэффициента от 1 обычно незначительны для качественного рассуждения.

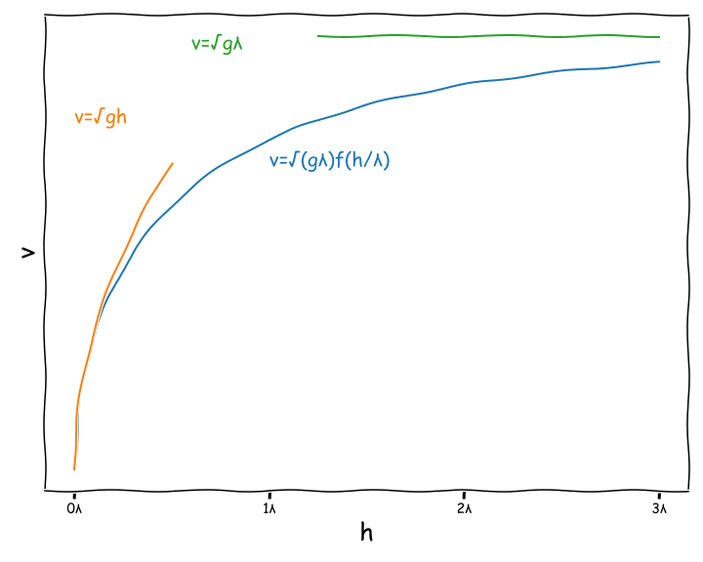
Рис. 2. График зависимости фазовой скорости волны \(v\) от глубины воды \(h\) при фиксированной длине волны \(\lambda\). Оранжевым и зеленым показаны предельные случаи \(h\ll \lambda\) и \(h \gg \lambda\). Примерный вид общего решения показан синим

Давайте подумаем, что происходит, когда волна под некоторым углом приближается к берегу. В простейшем случае, когда волна далеко от берега, глубина большая \(h\gg \lambda\) (правая часть графика на рис. 2) и скорость волны \(v=\sqrt{g\lambda}\). Когда же волна оказывается у берега, глубина становится меньше (в пределе \(h\ll \lambda\), что соответствует левой части графика на рис. 2) и \(v=\sqrt{gh}\).

Из школьной физики мы знаем, что, когда скорость волны в среде меняется, происходит преломление как показано на рис. 3. Это верно как для электромагнитных волн (света) при прохождении, например, сквозь стекло, так и для волн на поверхности воды. Таким образом, благодаря этому «преломлению» малая глубина вблизи берега играет роль своеобразной линзы, «фокусируя» волны так, что они обычно приходят почти параллельно берегу.

Рис. 3. «Преломление» морских волн по мере приближения к берегу

Во второй задаче воспользуемся уже полученным выражением \(v = \sqrt{g\lambda}\) (так как глубина воды большая), где \(v\) — фазовая скорость волны. Скорость корабля \(V\) связана со скоростью волны следующим образом: \(v = V\sin{\theta}\), где угол \(\theta\) изображен на рис. 4. Таким образом, скорость корабля равна:

Рис. 4. Кильватерные волны, порождаемые на поверхности воды плывущим кораблем

Более точное выражение, получаемое с помощью решения уравнений гидродинамики, отличается всего лишь на множитель \(\sqrt{2\pi}\):

Угол \(\theta\) равен примерно \(22^\circ\), а \(\lambda\approx 5{,}5\) м. Подставив, получим что скорость корабля составляет около \(30\) км/ч, или 15 узлов (что не очень быстро — возможно, это связано с близостью корабля к бухте).

В принципе, сама по себе пи-теорема — довольно тривиальное утверждение. По сути, это математическая формализация метода анализа размерностей, знакомого многим со школы. Она была доказана еще в конце XIX века, а затем была обобщена и применена к огромному количеству практических задач в физике уже в начале XX века. В англоязычной литературе пи-теорему называют по фамилии американского физика Эдгара Бакингема (Edgar Buckingham), который в 1914 году написал многостраничный обзор (E. Buckingham, 1914. On Physically Similar Systems; Illustrations of the Use of Dimensional Equations), с множеством примеров решения задач при помощи этой теоремы. Надо сказать, что в те времена утверждения, сходные с пи-теоремой в ее современной формулировке, встречались (по-видимому, независимо) в работах многих ученых. Например, в 1911 году ее для своих нужд сформулировал и доказал Дмитрий Рябушинский (D. Riabouchinsky, 1911. Мéthode des variables de dimension zéro et son application en aérodynamique).

Пи-теорема — это мощный инструмент, который помогает абстрагироваться от лишних деталей при решении физической задачи и значительно упростить ее математическую постановку. К примеру, в задаче с маятником, мы увидели, что переменных на самом деле не пять, а всего две: угол маятника \(\theta\) и некоторое эффективное время \(t\sqrt{g/l}\). Отдельно величины \(g\), \(l\) и \(t\) не несут никакого математического смысла, значение имеет только их комбинация, которую мы можем просто принять за новую меру времени (безразмерную) \(\tau = t\sqrt{g/l}\), забыв об этих параметрах. По сути, \(\tau\) является временем, измеренным в единицах периода некоторого маятника длиной \(l\) в земном поле притяжения.

Интересно, что в начале XX века точность изготовления маятниковых часов достигла такой степени, что в США они служили стандартом для определения времени с 1904 по 1929 год (см. Riefler escapement). Погрешность этих часов составляла 10 миллисекунд за сутки. Для сравнения, у современных атомных часов такая погрешность накопится примерно за миллион лет.

Эта теорема имеет также далеко идущие последствия в вычислительной физике. К примеру, представьте, что вам нужно смоделировать линзирование света черной дырой некоторой массы. Вместо того, чтобы решать задачу, измеряя расстояние в метрах или сантиметрах, можно измерять расстояния в радиусах Шварцшильда черной дыры \(r_g=2GM/c^2\) (где \(M\) — масса черной дыры). Все уравнения ОТО можно переписать в безразмерном виде, избавившись везде от \(r_g\) путем ввода новых координат \(x' = x/r_g\), \(y' = y/r_g\) и т. д. Тогда мы избавляемся от необходимости решать задачу несколько раз: решив ее единожды, это решение (в координатах «со штрихами», из которых легко перейти обратно в нормальные) будет применимо для черной дыры абсолютно любой массы. Или, например, решая уравнения гидродинамики для предсказания погоды на Земле, мы, по сути, решаем и задачу распространения термоядерного взрыва на поверхности нейтронной звезды, так как, опять же, характерные безразмерные коэффициенты там очень схожи.

Иными словами, пи-теорема абстрагирует физическую задачу, помогая перевести ее в плоскость математических уравнений с помощью введения безразмерных переменных. Это, хоть и не дает полное решение задачи, но бывает очень полезным для понимания характерных масштабов расстояний и времени и т. д., в которых имеет смысл решать задачу.