Падающие трубы

Представьте, что башня достаточно крепкая и не может сломаться. Что будет, если на верхний край такой башни положить кирпич? Оторвется ли он от поверхности во время падения?

Подумайте, с каким ускорением падают горизонтальные слои башни, находящиеся на разном удалении от основания.

Пусть \(L\) — полная длина трубы, \(r\) — радиус ее сечения, а \(m\) — масса. Для простоты мысленно разделим трубу на две части: нижнюю длиной \(xL\) и верхнюю длиной \((1-x)L\) (здесь \(x<1\)).

На верхнюю часть трубы помимо силы тяжести \(mg(1-x)\) действуют продольные силы (как показано на рис. 2) \(T_-\) и \(T_+\) и поперечная сила \(F\). Разделение продольных сил на \(T_-\) и \(T_+\), действующих с противоположных сторон сечения трубы, будет важно далее, когда мы будем считать натяжение.

Рис. 2.

Запишем уравнение движения Ньютона для верхней части трубы в поперечном направлении:

Здесь мы воспользовались тем, что труба как целое движется с угловой скоростью \(\omega\) и ускорением \(\dot{\omega}\) относительно основания, \((1+x)L/2\) — расстояние до центра тяжести верхней части трубы от основания, a \(\alpha\) — угол наклона трубы в данный момент относительно вертикали. Чтобы найти \(\dot{\omega}\), достаточно рассмотреть движение трубы как целое. Запишем уравнение для момента сил относительно основания:

где \(I\) — момент инерции трубы относительно основания, который для однородного распределения массы равен: \(I=\frac{1}{3} mL^2\). Отсюда найдем \(\dot{\omega}=3g\sin{\alpha}/(2L)\).

Подставив это в уравнение движения, можно получить следующее выражение:

Силы \(T_-\) и \(T_+\), как мы покажем далее, ответственны за «разлом» трубы на некоторой высоте \(xL\), где момент натяжения окажется максимальным. Запишем моменты сил относительно центра тяжести верхней части трубы:

где \(I_0 = \frac{1}{12} m(1-x)(1-x)^2L^2\) — момент инерции верхней части трубы массой \(m(1-x)\) и длиной \(L(1-x)\) относительно ее центра тяжести. Подставив \(F\), найдем:

Максимум этого выражения достигается при \(x=1/3\), что примерно соответствует наиболее вероятному месту разлома падающей трубы.

Заметим, что в разламывающее трубу натяжение мы не включили силу \(F\), предположив, что лишь натяжение из-за сил \(T_\pm\) ответственно за разлом. Это связано с тем, что сила \(F\) меньше \(T_\pm\) примерно в \(L/r\) раз (что много больше единицы).

Падение длинного предмета, у которого нижний конец закреплен, — очень интересный механический процесс. Такая система иногда называется обратным маятником, по аналогии с обычным маятником, который закреплен верхним концом. Если движение обычного маятника рассматривается практически в любом курсе механики в школе или университете, то механика обратного маятника почти никогда не изучается. Давайте исправим эту ситуацию и чуть-чуть поговорим о ней.

В задаче мы рассмотрели все ингредиенты, необходимые для описания движения такого маятника. Давайте вновь посмотрим на (угловое) уравнение движения трубы:

Угловую скорость относительно нижнего конца, \(\omega\), можно записать как \(\omega=\dot{\alpha}\) — это производная угла \(\alpha\) по времени (знак минус лишь задает направление вращения). Тогда, подставив \(I\) и проделав все сокращения, мы получим дифференциальное уравнение (второго порядка) относительно угла \(\alpha\):

Коэффициент 3/2 возникает из-за однородного распределения массы вдоль трубы. Если бы мы рассматривали классический обратный маятник, где вся масса сконцентрирована на верхнем кончике, то уравнение выглядело бы так: \(\ddot{\alpha}=(g/L)\sin{\alpha}\).

Первое, что можно заметить: при малых углах отклонения от вертикали \(\alpha\ll 1\) (так как \(\sin{\alpha}\approx \alpha\), если считать \(\alpha\) в радианах), выражение превращается в простое уравнение, схожее с уравнениями гармонических колебаний для обычного маятника, закрепленного сверху:

Вспомним, что уравнение гармонического колебания выглядит так: \(\ddot{x} =-\omega^2 x\), где \(\omega\) — частота колебаний. В нашем случае, правда, получается, что частота выражается мнимым числом. На этом аналогии с обычными маятниками не заканчиваются! Вместо колебаний, задаваемых суммой синусов и косинусов с частотой \(\omega\), мы получим экспоненциальное решение, задаваемое функциями \(e^{\omega t}\) и \(e^{-\omega t}\), где \(\omega = \sqrt{3g / (2L)}\):

где \(C_1\) и \(C_2\) — некоторые постоянные, зависящие от начальных условий. Если принять, что первоначальное отклонение балки равно \(\alpha(0) = \alpha_0\), а угловая скорость нулевая, \(\alpha'(0) = 0\), получим:

Подытожим. Для гармонических колебаний обычного маятника, задаваемых уравнением \(\ddot{x}=-\omega^2 x\), мы получаем зависимость от времени в виде синусов и косинусов, а для колебаний обратного маятника, задаваемых уравнением \(\ddot{x}=\omega^2 x\), решение выражается с помощью так называемых гиперболических косинусов и синусов! Это упрощенное решение, которое мы получили в предположении \(\sin{\alpha}\approx \alpha\), на самом деле довольно близко описывает полное решение уравнения (без приближения малых углов). Сравнение двух решений для начальных условий \(\alpha_0\approx 0{,}02\) показано на рис. 3 (время для удобства нормировано на величину \(\omega^{-1}=\sqrt{2L/(3g)}\)).

Рис. 3.

Пользуясь этим простым решением, можно достаточно точно оценить время падения трубы \(T\). Для этого достаточно приравнять \(\alpha(T)=\pi/2\). Получим \(T=(1/\omega)\cosh^{-1}{\left(\pi/(2\alpha_0)\right)}\), где \(\cosh^{-1}\) — это обратная функция к \(\cosh\) (по аналогии с \(\arccos\) и \(\cos\)). Если нарисовать график зависимости времени падения \(T\) от начального отклонения \(\alpha_0\), то можно увидеть очень интересную картину (рис. 4).

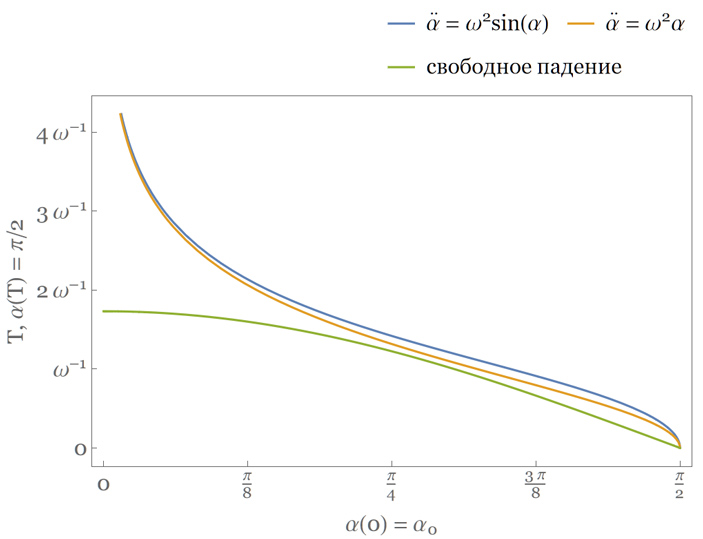
Рис. 4.

Очевидно, что чем меньше отклонение \(\alpha_0\), тем больше времени будет занимать падение (попробуйте убедиться сами с помощью эксперимента). Для сравнения, на графике также приведено время свободного падения предмета с высоты \(L \cos{\alpha_0}\), соответствующей начальному положению верхнего конца трубы (то есть обратного маятника). Что, опять же, неудивительно: свободно падающий предмет достигает земли быстрее, чем наш маятник.

Теперь мы имеем всю теорию, чтобы ответить на наводящий вопрос, поставленный в подсказке. Представьте, что нашим обратным маятником теперь является балка, один конец которой покоится на плоскости, а другой конец удерживается так, что балка находится в наклонном положении. Что произойдет, если на балку положить некий предмет, который не проскальзывает вниз в начальном положении, и затем отпустить конец балки? Оторвется ли этот предмет от поверхности балки во время ее падения?

Иными словами: будет ли верхний конец балки в какой-либо момент двигаться с большим ускорением, чем ускорение свободно падающего предмета?

Напрашивается отрицательный ответ, ведь и на балку и на блок действует одна и та же сила тяжести: было бы странно ожидать, что балка ускоряется как-то иначе.

Давайте ответим на этот вопрос математически. Линейная скорость верхнего конца балки в любой момент времени задается формулой \(v(t) = L\dot{\alpha}(t)= L \omega \alpha_0\sinh{\omega t}\) (производная \(\cosh\) равна \(\sinh\) и наоборот — даже проще, чем у \(\sin\) и \(\cos\), у которых иногда меняются знаки). Такая линейная скорость всегда направлена перпендикулярно балке, но нам, строго говоря, интересна лишь ее вертикальная компонента (направленная вниз), которую можно извлечь при помощи проецирования на вертикальное направление: \(v_{\rm вниз}(t)=L\dot{\alpha}(t)\sin{\alpha(t)}\). Чтобы ответить на вопрос, далее нужно найти вертикальное ускорение \(a_{\rm вниз}=\dot{v}_{\rm вниз}\). Выражение получается громоздким, поэтому мы не будем его здесь выписывать. Вместо этого приведем график зависимости \(a_{\rm вниз}\) от времени для нашего предыдущего случая \(\alpha_0\approx 0{,}02\) (рис. 5).

Рис. 5.

Из графика достаточно четко видно, что ближе к концу падения вертикальное ускорение становится больше \(g\)! Но верить не самым интуитивно ясным математическим выкладкам не обязательно — тот же самый эффект изящно можно продемонстрировать с помощью эксперимента (см. видео). Хорошо видно, что шарик, удерживаемый на краю наклонной балки с помощью пробки, в итоге оказывается в пластиковой чашке, закрепленной ниже. Такое было бы невозможно, если бы шарик никогда не отрывался от балки.

В качестве дополнительного упражнения подумайте о следующем: шарик, по сути, падает вертикально вниз, не ощущая присутствия балки во время падения. Для нашего случая, когда \(\alpha_0\approx 0{,}02\), это было бы невозможно, так как вертикальное ускорение края балки вначале меньше \(g\). При каком начальном отклонении демонстрация в видео возможна? В качестве визуальной мотивации на рис. 6 показаны три разных случая.

Рис. 6.