Физика самолетного гула

На рис. 1 внизу справа схематически показаны две отдельные характеристики спектрограммы, которые присутствуют почти на каждой из спектрограмм. Попробуйте услышать их в соответствующих аудиофайлах и понять, чем эти характеристики отличаются физически.

Самая яркая характеристика, которая выглядит как тонкая линия в спектрограмме, — это одна-единственная частота, которая меняется во время пролета самолета над звукозаписывающим устройством. Вторая характеристика — это некоторые гармоники (кратные частоты), которые ведут себя несколько иначе. Попробуйте понять, как и из-за чего они возникают.

Сперва разберемся с самой яркой из характеристик. В некоторых случаях, когда фоновый шум, издаваемый самолетом, не такой сильный (в основном это происходит, когда самолет летит близко, и высокие частоты издаваемые двигателем не поглощаются), на спектрограмме можно увидеть очень ярко выраженную характеристику на частотах от нескольких сотен до тысяч Гц. Частота этой характеристики уменьшается по мере пролета самолета над микрофоном из-за эффекта Доплера.

Давайте оценим, как меняется эта частота в зависимости от времени, и сравним полученные оценки с наблюдаемыми спектрограммами. Пусть самолет летит с постоянной скоростью \(v\) по горизонтальной прямой. Обозначим расстояние до ближайшей к микрофону (или наблюдателю) точки траектории \(h\) (иногда это число называют прицельным параметром), а угол между текущим положением самолета и перпендикуляром к его траектории — \(\alpha\) (рис. 2). Вычисления удобно проводить в безразмерных величинах. Поэтому введем следующие обозначения: безразмерная «скорость» самолета — \(\tilde{v}= v/c_s\) (где \(c_s\) — скорость звука\) и безразмерное «время» — \(\tilde{t}= t/(h/c_s)\).

Рис. 2.

Эффект Доплера связывает значение фиксированной частоты \(\nu_0\) с регистрируемой \(\nu\) следующим образом:

где \(v_{||}\) — компонента скорости в направлении к наблюдателю. В нашем случае, если обозначичить \(\tilde{\nu}= \nu/\nu_0\), получим: \(\tilde{\nu}=1+\tilde{v}\sin{\alpha}\). С другой стороны, \(\tan{\alpha}=-vt/h=-\tilde{v}\tilde{t}\), где \(t=0\) соответствует ближайшей точке траектории самолета к микрофону (или наблюдателю). Тогда, избавившись от \(\alpha\), можно выразить наблюдаемую частоту в зависимости от времени:

На рис. 3 показана эта зависимость для значения \(v/c_s = \tilde{v} = 0{,}3\) (≈200 узлов).

Рис. 3. Доплеровское смещение частоты в зависимости от положения самолета относительно наблюдателя. Интерактивная версия доступна здесь

В общем случае характерная ширина кривой будет пропорциональна \(h\), тогда как высота (амплитуда изменения частоты), будет пропорциональна скорости самолета \(v\) (рис. 4).

Рис. 4.

На рис. 5 показаны аналитические кривые с соответствующими параметрами для трех случаев, когда эта доплеровская характеристика видна. Для оценки принималось \(c_s=330\) м/с.

Рис. 5.

Как видно, наблюдаемая зависимость частоты от времени хорошо согласуется с графиками, построенными по формулам. Из этого можно сделать вывод, что наша упрощенная модель неплохо работает.

Вторая частотная характеристика — почти параболические широкие линии кратной частоты. Она не может описываться эффектом Доплера, так как после пролета самолета мимо наблюдателя их частота растет. Оказывается, такой эффект получается благодаря интерференции прямого звука от самолета и отраженного от поверхности Земли.

Снова рассмотрим простую модель: самолет летит по прямой на постоянной высоте \(H\) от поверхности. Обозначим через \(l\) рост наблюдателя (или, если запись делается с помощью камеры/микрофона, это будет высота штатива). Расстояние от проекции самолета на поверхность до наблюдателя обозначим \(D\). Достаточно просто показать, что расстояние, которое пролетает звуковой сигнал от самолета к наблюдателю (точнее, к его уху) по прямой, равно \(\sqrt{(H-l)^2+D^2}\), а расстояние, которое пролетает сигнал, отраженный от поверхности, равно \(\sqrt{H^2+D^2}\).

Рис. 6.

Положительная интерференция (амплитуды волн складываются, усиливая сигнал) происходит, когда в разность пройденных путей \(\Delta s\) помещается целое число длин волн \(\lambda\). Давайте оценим эту разность. Обозначим для краткости \(S= \sqrt{H^2 + D^2}\). Тогда

Так как рост наблюдателя (как и высота обычного штатива) много меньше расстояний \(H\) и \(S\), членом \(l^2\) можно пренебречь, а корень можно раскрыть, воспользовавшись приближением \(\sqrt{1-x}\approx 1-x/2\) для \(x\ll 1\). Получим, что \(\Delta s\approx Hl/\sqrt{H^2 + D^2}\). Положительная интерференция возникает, когда:

где \(n\) — натуральное число. Из этого выражения очевидно, что если в промежуток \(\Delta s\) помещается целое число длин волн \(\lambda\), то то же самое верно и для частот \(\lambda/2\), \(\lambda/3\), и т. д. (или, если смотреть на частоты, для частот \(\nu=c_s/\lambda\), \(2\nu\), \(3\nu\) и т. д.).

Посмотрим, как выглядит амплитуда сигнала в зависимости от частоты при фиксированных значениях \(\Delta s\). Для этого просуммируем две синусоиды с одинаковой частотой и амплитудой, но с фазой, отличающейся на \(2\pi\Delta s/\lambda\):

График этой амплитуды (в квадрате) от частоты выглядит так, как показано на рис. 7 (для этого примера взяты значения \(\Delta s=1\) м и \(s=20\) м. Быстрые колебания амплитуды от частоты нас не интересуют, так как эффективно они будут усредняться записывающим устройством или ухом. Характерное расстояние между пиками для этих изменений равно \(\Delta \nu = c_s / (2 s+\Delta s)\approx c_s/(2s)\). Однако огибающая этого графика (синяя кривая на рис. 6) имеет очевидные минимумы и максимумы, расстояние между которыми — \(\Delta \nu = c_s / \Delta s\) (в нашем случае это около 330 Гц).

Рис. 7.

По мере движения самолета значение \(\Delta s\) меняется, меняя характерное расстояние между максимумами \(\Delta \nu\), благодаря чему мы и видим сперва уменьшение частоты пиков в спектрограмме, а затем — увеличение. Если самолет пролетает непосредственно над наблюдателем, пиковые частоты будут соответствовать значениям \(n c_s / l\) (где \(n\in\mathrm{N}\)). Таким образом, «белый шум» от самолета (то есть звук, излучаемый в широком диапазоне частот) будет менять амплитуду в зависимости от частоты из-за интерференции сигнала на разных частотах: некоторые частоты будут усиливаться, а некоторые — напротив — подавляться. Заметим также, что эта характеристика не зависит от направления скорости самолета, поэтому спектрограмма получается симметричной относительно момента пролета (в отличие от доплеровской характеристики).

Чтобы нарисовать финальный вид теоретической спектрограммы, учтем также, что воздух поглощает звук, причем чем выше частота — тем больше коэффициент поглощения. Если умножить амплитуду на экспоненциальный коэффициент с зависимостью от частоты \(\exp{\left[-(\nu/300~\text{Гц})\cdot s / (1~\text{км})\right]}\) для значений \(c_s\approx 330\) м/с, \(l\approx 1\) м, \(v\approx 120\) км/ч и \(H\approx 120\) м и предположить, что вдобавок к белому шуму двигатель самолета производит характерный звук на частоте 2 кГц, получим аналитическую спектрограмму, показанную на рис. 8.

Рис. 8.

Если вы когда-нибудь наблюдали за движением самолетов во время полета (это можно делать, например, при помощи сайта flightradar24.com) — особенно при перелетах над океаном, то могли заметить, что иногда происходит нечто очень странное: скорость некоторых из самолетов, судя по показаниям, может превышать ~650 узлов (1200 км/ч). При этом скорость звука на высоте 5–10 км варьируется в районе 580–600 узлов (300–310 м/с или 1070–1110 км/ч). Означает ли это, что пассажирские лайнеры могут лететь со сверхзвуковой скоростью? И если это так, то почему пассажиры не чувствуют характерный щелчок от ударной волны?

Ответ, на самом деле, кроется в определении «скорости» самолета. Скорость, которая обычно регистрируется диспетчерами (и, в частности, указывается на flightradar24.com), — это так называемая путевая скорость (ground speed), то есть скорость, с которой самолет перемещается относительно поверхности Земли. Но нужно помнить, что воздух не находится в состоянии покоя: на высоте 5–10 км скорость ветра может достигать 100–200 узлов. Такой эффект сильных высотных ветров наблюдается в довольно узкой области, расположенной между границами полярных и субтропических широт, которая называется высотным струйным течением (jet stream; посмотреть, как это выглядит, можно, например, здесь).

Рис. 9. Высотные струйные течения формируются благодаря сильному градиенту температуры и давления, возникающему в местах «соприкосновения» конвекционных потоков от двух воздушных масс с сильно отличающимися характеристиками. Рисунки с сайта noaa.gov

Таким образом, путевая скорость воздушного судна (векторно) складывается из скорости самого самолета относительно воздуха, и скорости воздуха (ветра) относительно Земли. Для сверхзвукового движения имеет смысл лишь первая компонента, так как скорость звука измеряется в системе покоя воздуха. Скорость современных пассажирских самолетов относительно воздуха редко превышает 80–90% от скорости звука. Поэтому никакого сверхзвукового щелчка ожидать не стоит, так как звук в воздухе все еще движется быстрее самолета. Но если скорость ветра относительно Земли достаточно высокая, а его направление совпадает с направлением движения самолета (попутный ветер), то суммарная скорость (путевая) запросто может превысить формальную скорость звука.

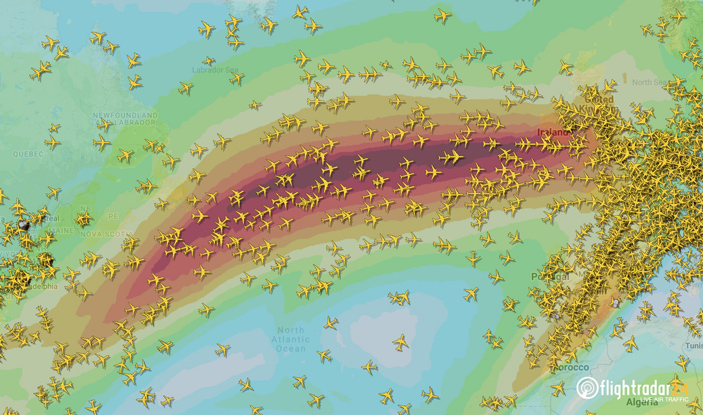
Рис. 10. При прокладывании маршрутов для пассажирских самолетов (особенно на трансатлантических направлениях) учитывается наличие на пути струйных течений и скорость ветра в них. По возможности самолеты летят с сильным попутным ветром — это помогает сэкономить топливо и зачастую пролететь маршрут быстрее запланированного. Рисунок из твиттера Flightradar24

Иногда, если скорость самолета достаточно мала, можно наблюдать и обратное явление: при встречном ветре, скорость которого равна скорости самолета, путевая скорость самолета окажется примерно нулевой, и он, по сути, будет просто висеть в воздухе.