Отражение в ионосфере

Представьте промежуточный момент, когда заряды из некоторой области \(\Delta x\) собрались в одну бесконечную заряженную плоскость. Электрическое поле от такой плоскости с плотностью заряда \(\sigma\) (заряд на единицу площади) однородно и равно \(E=2\pi\sigma\) (этот факт мы докажем в послесловии). Посчитайте сперва заряд на единицу площади такой плоскости, а затем — и электрическое поле.

Вспомним из задачи Гравитационный поезд, что при действии квазиупругой силы \(F = k x\), где \(x\) — смещение от состояния равновесия, а \(k\) — некоторый коэффициент пропорциональности, возникают гармонические колебания с частотой \(\omega=\sqrt{k/m}\).

Рассмотрим промежуточный момент, когда частицы с положительными и отрицательными зарядами из области \(\Delta x\) вокруг положения равновесия разлетаются в противоположные стороны как показано на рис. 3.

Рис. 3. Заряженные частицы в плазме сконцентрированы на некотором расстоянии \(\Delta x\) от центра области, эта ситуация приведена в два различных момента времени. Насыщенность цвета показывает общий нескомпенсированный заряд областей, а длина вектора \(\mathbf{E}\) пропорциональна величине генерируемого электрического поля

Очевидно, что чем больше \(\Delta x\) — тем больше нескомпенсированного заряда в областях (частицы «собираются» из большей области). Если в среднем концентрации зарядов разных знаков равны \(n_e=n_p\), то заряд на единицу площади у таких промежуточных областей будет равен: \(\sigma = \Delta x n_e q\) (так как концентрируются заряды с расстояний \(\Delta x/2\) с каждой стороны). На рис. 4 все это показано в динамике.

Рис. 4. Периодическое колебание концентрации зарядов в плазме. В зависимости от того, какого знака заряды собираются на удалении от центра области, меняется знак электрического поля

Таким образом, в любой промежуточный момент в плазме мы имеем заряженные (бесконечные) плоскости чередующихся знаков с зарядом на единицу площади равным \(\sigma = \pm \Delta x n_e e\) (\(e = |q_e| = q_p\) — это абсолютная величина заряда электрона и протона).

Электрическое поле, которое генерируется в результате такого нарушения нейтральности равно \(E = 4\pi\sigma\) (так как вместо одной плоскости у нас по сути две с разными знаками). Сила, действующая на отдельно взятый электрон при этом равна \(F = eE = 4\pi n_e e^2 \Delta x\). Заметим, что сила — квазиупругая, так как она пропорциональна смещению \(\Delta x\). В этой ситуации, как мы помним, возникают гармонические колебания с частотой

где \(m_e\) — масса электрона. Важно заметить, что плазменная частота зависит лишь от концентрации заряженных частиц.

Внимательный читатель мог заметить, что у электронов и протонов разные массы и плазменная частота электронов будет отличаться от плазменной частоты протонов. Поэтому рисунки 2, 3 и 4 относятся скорее к электрон-позитронной плазме, в которой массы зарядов равны. В электрон-протонной плазме электроны колеблются примерно в 44 раза чаще, чем протоны. Но благодаря этому, несмотря на разность масс, все вычисления верны, поскольку протоны можно считать покоящимися, а наличие или отсутствие электронов в некоторой области будет создавать отрицательный или положительный заряд в этой области.

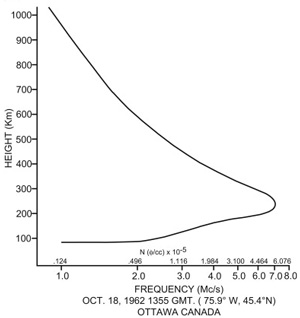
Рис. 5. Зависимость плазменной частоты (и концентрации заряженных частиц) в ионосфере от высоты над поверхностью Земли. Рисунок с сайта sciencedirect.com

Для ионосферы Земли с характерной концентрацией \(10^5\) частиц на кубический сантиметр, можно оценить, что плазменная частота соответствует около 15 МГц: частоты ниже этого значения будут отражаться от ионосферы, а частоты выше будут проходить сквозь плазму, преломляясь по пути. Так как концентрация в ионосфере на разных высотах разная, радиосигналы каждой частоты будут отражаться разными слоями ионосферы. Зная время отправления и прибытия сигнала, а также ее частоту, таким образом можно «картографировать» ионосферу, исследуя концентрацию частиц в ней на разных высотах над поверхностью Земли.

Такое отражательное свойство ионосферы используется даже для коммуникации. В 1901 году именно с помощью этого эффекта была реализована первая трансатлантическая радиопередача итальянцем Гульельмо Маркони.

Рис. 6. Радиопередача с помощью отражения в ионосфере. Рисунок с сайта electronics-notes.com

Вернемся к физике. Почему же электромагнитные волны с частотами ниже частоты плазменных колебаний отражаются? По сути, плазменная частота (или, если угодно, период) показывает характерное время, за которое заряженные частицы плазмы способны коллективно перемещаться, компенсируя внешние электрические поля.

Если частота изменения внешнего электрического поля слишком большая (колебания поля слишком быстрые), то частицы просто не успевают перестроиться и скомпенсировать это поле, из-за чего такой сигнал может без труда пройти сквозь плазму. Когда частота сигнала мала, то за время колебания частицы успевают среагировать на изменение поля и компенсируют его. Тем самым сигнал «выталкивается» из плазмы, отражаясь от нее.

Можно сказать, что для частот меньше плазменной, плазма ведет себя как проводник (вспомним из школьной физики, что в проводнике заряды всегда успевают перестроиться и скомпенсировать внешнее поле), а для больших частот — как диэлектрик.

Однако плазма — это не просто некоторая экзотическая форма вещества, в которой находится вещество где-то там в космосе (или, например, при ионизации воздуха пламенем и т. д.). Проводящие электроны в самом обычном металле также являются плазмой: они абсолютно так же не связаны с ионами в кристаллической решетке и обладают очень схожими свойствами с обычной плазмой. У плазмы в металлах тоже есть плазменная частота. К примеру, для алюминия или серебра с характерной концентрацией электронов \(10^{23}~\text{см}^{-3}\) эта частота приходится на ультрафиолетовый диапазон электромагнитных волн. Отсюда следует, что волны, частоты которых ниже (к примеру — оптические), отражаются металлами, что и придает последним характерный блеск (см. также задачу Металлический блеск кремния).

Как и было обещано, давайте вычислим поле однородно заряженной бесконечной плоскости. Для этого воспользуемся замечательной теоремой Гаусса, которая очень часто используется физике.

Допустим, у нас есть некий произвольный набор зарядов — как положительных, так и отрицательных — произвольно распределенных в пространстве (рис. 7, слева). Такое распределение зарядов будет образовывать некоторое сложное электрическое поле.

Рис. 7. Наглядная иллюстрация теоремы Гаусса

Окружим эти заряды некоторой поверхностью, опять же, произвольной формы, так, чтобы все заряды лежали внутри этой поверхности (рис. 7, в середине). Разделим поверхность на маленькие (в идеале — бесконечно малые) кусочки, каждый из которых имеет площадь: \(A_1\), \(A_2\), ... Возьмем произвольный из этих маленьких кусочков, \(A_i\), и посчитаем компоненту электрического поля, \({E}_i\), перпендикулярную поверхности в этом месте — \(E_{i\perp}\) (рис. 7, справа).

Теперь просуммируем по всем кусочкам значения \(A_i E_{i\perp}\). Эта сумма называется потоком электрического поля через замкнутую поверхность. По сути, если думать об электрическом поле как о поле скоростей некоторой жидкости, эта сумма будет иметь физический смысл суммарного потока жидкости через замкнутую поверхность.

Теорема Гаусса говорит о том, что суммарный поток электрического поля через замкнутую поверхность всегда равен суммарному заряду вещества внутри этой поверхности, помноженному на \(4\pi\).

В общем случае произвольно сложного распределения зарядов эту теорему очень тяжело применить, однако в некоторых случаях с простым распределением она помогает решать относительно сложные задачи довольно быстро. Наш случай с бесконечной равномерно заряженной плоскостью как раз такой.

Во-первых, очевидно, что электрическое поле такой плоскости всегда перпендикулярно ей, так как нет никакого нарушения симметрии. Зная это, давайте выберем некую замкнутую область так, чтобы легко было посчитать поток поля сквозь нее. Если мы выберем эту область в виде цилиндра, как показано на рис. 8, то поток сквозь боковые стенки цилиндра будет равен нулю (так как поле параллельно этим стенкам), а потоки сквозь верхнюю и нижнюю грани равны \(AE\), где \(E\) — величина поля у основания, а \(A\) — площадь основания.

Рис. 8. Электрическое поле бесконечной равномерно заряженной плоскости

Суммарный заряд, содержащийся внутри этой области, тоже легко можно посчитать: он равен произведению площади на плотность заряда \(\sigma\). Теорема Гаусса дает равенство \(2AE = 4\pi A\sigma\), откуда \(E=2\pi\sigma\). Видно, что, во-первых, поле не зависит от выбора области, через которую считается поток, а во-вторых, поле не зависит от расстояния до плоскости: оно однородно в обе стороны от нее.

Примечательно, что теорема Гаусса применима не только к электрическому, но и к гравитационному полю. Только вместо потока электрического поля нужно взять поток гравитационного поля, а вместо суммарного заряда — суммарную массу в области. Попробуйте, вооружившись теоремой Гаусса, доказать утверждение из задачи Гравитационный поезд о том, что гравитационное поле внутри полой сферы с равномерным распределением массы по поверхности тождественно равно нулю (воспользуйтесь сферической симметрией, чтобы правильно подобрать область).