Окружности и гиперболы
Задача
На координатной плоскости расположены гиперболы вида |xy| = k и окружности вида x2 + y2 = 2k. В обеих формулах натуральное число k пробегает все значения от 1 до n. На сколько частей все эти линии делят координатную плоскость при n = 22?
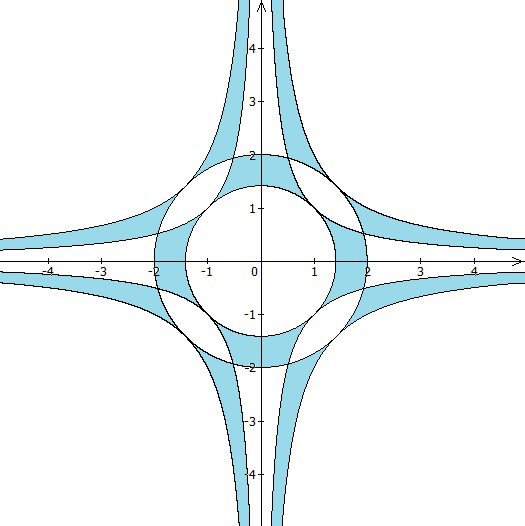
Например, при n = 2 плоскость разбивается на 25 частей (рис. 1).
Подсказка 1
Непосредственным счетом при малых значениях n можно найти число частей разбиения плоскости указанными линиями, заметить закономерность в полученных числах, а затем доказать эту закономерность.
Подсказка 2
Можно разделить все части разбиения плоскости на несколько групп, с таким расчетом, чтобы в каждой группе было удобно считать части, после чего просуммировать полученные числа.
Решение
При конкретном значении \(k\) данные уравнения задают в координатной плоскости три линии: уравнение \(|xy|=k\) задает две гиперболы \(xy=k\) и \(xy=-k\), а уравнение \(x^2+y^2=2k\) задает окружность с центром в начале координат и радиусом \(\sqrt{2k}\). При этом окружность касается обеих ветвей каждой гиперболы в точках \((\sqrt k; \sqrt k)\), \((\sqrt k; -\sqrt k)\), \((-\sqrt k; \sqrt k)\) и \((-\sqrt k; -\sqrt k)\).
Решим задачу в общем виде, когда число \(k\) пробегает натуральные значения от 1 до \(n\). Пусть на плоскости построены \(n\) окружностей и \(2n\) гипербол, которые делят плоскость на \(K_n\) частей. Обращаем внимание, что оси координат не являются линиями деления! Разобьем все эти части плоскости на несколько групп с таким расчетом, чтобы в каждой группе было удобно считать части.

Рис. 2.
На рис. 2 показан один из возможных вариантов разбиения, части каждой группы окрашены одним цветом. Посчитаем число частей в каждой из групп:
1) зеленый «крест» в центре состоит из окружности и четырех «лучей» в каждом из которых \(n-1\) часть, то есть этот «крест» содержит \(4(n-1)+1=4n-3\) части;
2) синие «хвосты»: их четыре, в каждом по \(2n-1\) частей; итого — \(8n-4\);
3) белые «диагонали»: в каждом квадранте их столько же, сколько гипербол, то есть \(n\); итого — \(4n\);
4) желтые «клетки»: видно, что они разбиваются на 8 равных подгрупп, в каждой из которых «клетки» расположены в виде треугольника, то есть их количество в подгруппе выражается треугольным числом, а именно, \(T_{n-2} = \frac{(n-1)(n-2)}{2}\).
Значит, \(K_n=(4n-3)+(8n-4)+(4n)+8\cdot\frac{(n-1)(n-2)}{2}\). После упрощения получим \(K_n=4n^2+4n+1=(2n+1)^2\).
Если кому-то предложенный вывод формулы для \(K_n\) показался неубедительным, давайте проверим результат с помощью метода полной математической индукции.
В самом деле, при \(n=1\) две гиперболы и касающаяся их окружность делят плоскость на 9 частей, то есть \(K_1=(2\cdot1+1)^2=9\) и база индукции выполняется (рис. 3, слева).

Рис. 3.
Докажем индукционный переход. Предположим, что верна формула \(K_n=(2n+1)^2\), и покажем, что тогда \(K_{n+1}=(2n+3)^2\). Действительно, на \((n+1)\)-м шаге добавляются еще две гиперболы и одна окружность (рис. 3, справа). Эти линии добавляют по \((2n+2)\) частей с каждой из четырех сторон (выделены синим на рис. 3), то есть всего\((8n+8)\) частей, поэтому \(K_{n+1}=K_n+8n+8=(2n+1)^2+8n+8=(2n+3)^2\). Это решение предложил мой ученик Илья Быкадоров (11 класс).
Остается вычислить число частей плоскости при \(n=22\): \(K_{22}=(2\cdot22+1)^2=45^2=2025\) частей. Пусть этот ответ будет заключительным аккордом уходящему году!
Послесловие
Часто мои задачи первыми решают мои ученики. Данная задача удивила большим количеством различных решений, предложенных участниками нашего математического кружка. Выше были приведены два решения, а сейчас я предлагаю вам познакомьться с еще несколькими решениями и небольшими комментариями к ним.
Решение №3 (Александр Юресько). Рассмотрим области, на которые плоскость разбита ветвями двух внешних гипербол \(|xy|=n\) и наибольшей окружностью \(x^2+y^2=2n\). Границы этих областей выделены красным на рис. 4. В каждой зеленой области вместе с ее границами расположено \(2n\) ветвей гипербол, которые делят каждую зеленую область на \(2n-1\) частей.

Рис. 4.
Рассмотрим синюю область, ограниченную красной окружностью. В ней в самом центре находится окружность, соответствующая \(k=1\), и между этой окружностью и самой внешней окружностью расположено \(n-1\) кольцо (кольцо — это область между двумя соседними окружностями).
Посчитаем количество частей в этих кольцах. В первом кольце 8 частей, во втором — 16 частей, в третьем — 24 части, и так далее: в каждом следующем кольце число частей разбиения на 8 больше. Почему? Объяснить это можно следующим образом. Пусть в координатной плоскости построены \(n\) окружностей, а гиперболы пока не построены. Гиперболы будем рисовать парами для каждого \(k\), начиная с \(k=1\). Ветви гипербол при \(k=1\) делят первое кольцо и все остальные кольца на 8 частей. Ветви гипербол при \(k=2\) уже не делят первое кольцо, но все остальные кольца делят, увеличивая число частей на 8, то есть делят их на 16 частей. Ветви гипербол при \(k=3\) не делят первое и второе кольцо, но все остальные кольца делят, увеличивая число частей в каждом кольце на 8, то есть делят их на 24 части, и так далее. Таким образом, с увеличением \(k\) в каждом кольце частей получается на 8 больше, чем в предыдущем. Значит, числа частей в кольцах — это члены арифметической прогрессии с разностью 8 и первым членом 8.
Тогда число частей плоскости в синей области равно сумме членов этой арифметической прогрессии плюс 1, поскольку есть еще круг в самом центре. То есть, надо вычислисть сумму \(1+8+16+\ldots+8(n-1)\), она равна \(4n^2-4n+1\).
Окончательно получим, что плоскость делится гиперболами и окружностями на \(4(2n-1)+(4n^2-4n+1) + 4 = 4n^2+4n+1\).
Но многое зависит от способа разбиения плоскости на отдельные области. В этом можно убедиться, познакомившись с еще одним решением. Его автор придумал разбиение плоскости на области, которое позволяет очень быстро найти окончательный ответ.
Решение №4 (Даниил Нерух). Выделим зеленым цветом четыре одинаковые области (рис. 5). Подсчет частей плоскости в каждой из них начнем с внутреннего кольца (самого светло-зеленого), потом добавим части соседнего кольца, и так далее — суммируем до последнего самого большого кольца. К полученной сумме добавим части плоскости, расположенные между ветвями \(2n\) гипербол, — их \(2n-1\) частей. Значит, зеленые области содержат \(1+3+5+\ldots+(2n-1)\) частей. Но, как известно, сумма \(n\) первых нечетных чисел равна \(n^2\). Белые части легко посчитать, их \(4n+1\). В итоге, после суммирования получается, что эти гиперболы и окружности делят плоскость на \(4n^2+4n+1\) часть.

Рис. 5.
Как интересно получается: разные группировки частей плоскости дают при суммировании совершенно одинаковые слагаемые. Убедитесь в этом при знакомстве со следующим решением.
Решение №5 (Артём Реуцкий). Разобьем плоскость на пять областей: четыре красные и одну желтую (рис. 6). Каждая красная область одинаково делится на части указанными линиями. Например, в левой верхней области части плоскости можно посчитать группами, находящимися между соседними гиперболами, и получим в каждой красной области \(1+3+5+\ldots+(2n-1)\) частей, если считать сверху вниз по диагонали рисунка, а эта сумма равна \(n^2\). В желтой области имеется центральный круг, а \(n\) окружностей делят каждое «крыло» на \(n\) частей, поэтому в желтой области \(4n+1\) часть. Итого получается, что плоскость всеми гиперболами и окружностями делится на \(4n^2+4n+1\) часть.

Рис. 6.
Удивительно, что даже совсем очевидная «шахматная» раскраска частей плоскости позволяет организовать подсчет частей плоскости в нашей задаче.
Решение №6 (Арина Авилова). Раскрасим все части плоскости, разбиваемой \(n\) окружностями и \(2n\) гиперболами в шахматном порядке (рис. 7). Посчитаем синие части плоскости в правом «крыле», считая их группами в кольцах, получим \(1+2+3+\ldots+n=\frac{n(n+1)}{2}\) частей. Значит, всего синих частей будет \(4\cdot\frac{n(n+1)}{2}=2n^2+2n\). Посчитаем белые части плоскости в правом «крыле», считая их группами в кольцах, начиная от центра, получим \(1+2+3+\ldots+n-1=\frac{n(n-1)}{2}\) частей. Остались непосчитанными белые части, расположенные вдоль «диагоналей» на рис. 7, понятно, что их \(4n+1\). Всего же количество белых частей равно \(4\cdot\frac{n(n-1)}{2} +4n+1=2n^2+2n+1\). Сложив число синих и белых частей плоскости, снова получим \(4n^2+4n+1\) частей.

Рис. 7.
После того, как ребята предложили столько различных решений, мне, их учителю, тоже хотелось удивить своих учеников оригинальным решением задачи. Мне удалось придумать «топологическое» решение, не похожее ни на одно из предыдущих.
Решение №7. На рис. 8 слева изображены две гиперболы \(xy=1\) и \(xy=-1\) и окружность \(x^2+y^2=2\). Координатную плоскость в этом решении ограничим квадратом. Эти две гиперболы и касающаяся их окружность делят этот квадрат на 9 частей. Заметим, что если окружность заменить квадратом, а ветви гиперболы — прямыми углами, то плоскость по-прежнему будет разбита на 9 частей (рис. 8, справа). Другими словами, деление плоскости двумя гиперболами и касающейся их окружностью равносильно (по числу получающихся частей) делению плоскости двумя парами перпендикулярных прямых.

Рис. 8.
Так же можно поступить при любом \(k\), то есть при каждом \(k\) две гиперболы и соответствующая им окружность заменяется на две пары перпендикулярных прямых. На рис. 9 изображен результат замены гипербол и соответствующих им окружностей при \(n=3\) прямыми. В этом случае плоскость разбивается шестью параллельными прямыми одного направления и шестью прямыми перпендикулярного направления, которые делят плоскость на \(7^2=49\) частей.
В общем виде, если число \(k\) пробегает все целые значения от 1 до \(n\), то в каждой группе будет по \(2n\) параллельных прямых, которые делят плоскость на \((2n+1)^2\) частей.

Рис. 9.
Последнее решение позволяет утверждать, что в нашей задаче число частей разбиения плоскости равно в точности числу клеток на шахматной доске размером \((2n+1)\times(2n+1)\), и рис. 7 с шахматной раскраской плоскости можно рассматривать как специальным образом деформированную шахматную доску. Отсюда вытекает еще один способ подсчета числа частей плоскости как числа «клеток» в деформированной шахматной доске, по «кривым рядам» (рис. 10). Ряды пронумерованы числами от 1 до \(2n+1\), в каждом ряду \(2n+1\) «клеток», поэтому всего «клеток», то есть частей разбиения плоскости получается \((2n+1)^2\).

Рис. 10.
Будет ли продолжение в этой коллекции решений нашей задачи? Предлагайте свои новые решения, уважаемые читатели!
Последние задачи














Рис. 1.