Способности магнитного монополя
Законы, описывающие электрические и магнитные поля, очень похожи, и вместе они составляют единую систему уравнений. Однако в одном аспекте эти поля сильно отличаются: электрических зарядов вокруг полным-полно, а магнитных монополей (так называют отдельные магнитные заряды) нет. Нет ли их совсем, или же они есть, но просто нам до сих пор не встретились — вопрос открытый, но, по крайней мере, вся та электродинамика, которая используется в физике, технике и повседневной жизни, построена на предположении, что магнитных монополей в природе не существует.
Тем не менее теорфизики — люди смелые и вполне могут заинтересоваться теоретическим описанием какого-то явления, даже если оно в реальном мире не наблюдается. Просто, когда изучаешь такие ситуации, можно узнать что-то новое о самих уравнениях электродинамики и почувствовать, в чем состоит необычность этих гипотетических явлений. Кроме того, не надо зарекаться: может быть, этот опыт пригодится в дальнейшем, если физики сумеют обнаружить явление, в чем-то напоминающее наше гипотетическое. Забегая вперед, скажем, что это отношение полностью оправдывается в случае магнитных монополей: уже сейчас есть экспериментальные результаты, которые удобно описывать в терминах «эффективных» магнитных монополей.
Попробуем быть смелыми и мы и решим задачку, которая иллюстрирует одно занятное свойство магнитного монополя.
Итак, что такое магнитный монополь? По аналогии с электрическим зарядом, это некий точечный источник магнитного поля. Магнитное поле от неподвижного монополя выглядит так же, как электрическое поле от неподвижного электрического заряда: линии поля радиально расходятся от источника во все стороны, а напряженность поля ослабевает при удалении от него обратно пропорционально квадрату расстояния (рис. 1). Взаимодействие двух магнитных монополей тоже было бы похоже на взаимодействие двух электрических зарядов: одноименные заряды отталкиваются, разноименные притягиваются. Теперь усложним вопрос: как будет магнитный монополь действовать на электрический заряд? Если обе частицы покоятся, то никак, ведь магнитный монополь создает только магнитное поле, а электрический заряд — только электрическое, и в электро- и магнитостатике они друг на друга не действуют. А что будет, если они движутся друг относительно друга?
Задача
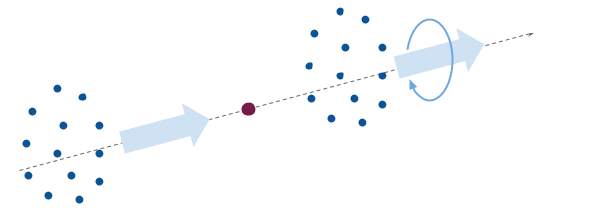
Рис. 2. Облако зарядов налетает на неподвижный магнитный монополь. Докажите, что после пролета облако закручивается вокруг оси движения
Рассмотрим неподвижный магнитный монополь, на который издалека налетает «облако» из точечных электрических зарядов (рис. 2). Начальные скорости всех зарядов были равны и параллельны друг другу, так что облако двигалось как единое целое (электрическим взаимодействием между частицами этого облака пренебрегаем). Докажите, что после пролета сквозь монополь это облако, помимо прочего, начнет вращаться вокруг оси первоначального движения. Для простоты считайте, что угол отклонения каждого заряда в поле монополя мал.
Подсказка
Раз электрическим взаимодействием между зарядами предлагается пренебречь, то некий эффект должен проявляться для каждой частицы по отдельности, а уже потом он визуально сложится во вращение всего облака. Поэтому начните с упрощенной задачи: мимо монополя на некотором расстоянии пролетает одна заряженная частица. Выясните, какая сила на нее действует, куда эта сила направлена и как она повлияет на траекторию частицы. Затем представьте несколько частиц, двигающихся параллельными курсами, и проследите изменение траектории для каждой из них и уже после этого представьте себе совокупное поведение всего облака.
Решение
На заряженную частицу, двигающуюся в магнитном поле B, действует сила Лоренца:

Напряженность магнитного поля от монополя выражается формулой:
![]()
Здесь ![]() обозначает единичный вектор, направленный от монополя к заряду. Обе эти формулы записаны в естественной системе единиц СГС, которая удобна для описания электромагнитных явлений. Если вторую формулу подставить в первую, то получится сила, действующая на пролетающую частицу.
обозначает единичный вектор, направленный от монополя к заряду. Обе эти формулы записаны в естественной системе единиц СГС, которая удобна для описания электромагнитных явлений. Если вторую формулу подставить в первую, то получится сила, действующая на пролетающую частицу.

Рис. 3. Сила, действующая на заряд, пролетающий мимо магнитного монополя
В этой задаче нас интересуют не сами эти формулы, а то, куда направлена сила. Пусть частица пролетает так, как показано на рис. 3. Мы знаем по условию, что траектория отклонится не сильно, но не знаем, в какую именно сторону. Ответ на этот вопрос как раз и дают написанные выше формулы. Они говорят, что направление силы определяется векторным произведением скорости и единичного радиус-вектора. Если частица движется, как на рисунке 3, то оба этих вектора лежат в плоскости рисунка (и не параллельны друг другу), а значит, их векторное произведение направлено перпендикулярно плоскости рисунка. Для верхней траектории это направление от рисунка на нас, для нижней траектории — от нас вглубь рисунка. Этот вывод справедлив для любых точек траектории. Поэтому когда эти частицы пролетят мимо монополя, их траектории отклонятся в ту же сторону, т.е. они выйдут из плоскости рисунка, одна чуть выше, другая чуть ниже (рис. 4).

Рис. 4. Сила со стороны монополя разводит пару частиц в стороны, как бы закручивая ее вокруг оси движения
Аналогично действуем для любой другой частицы: надо лишь представить себе новую плоскость (она задается векторами скорости и ![]() ) и отклонить траекторию из этой плоскости. Траектория каждой частицы будет отклоняться в одну сторону, например вправо, по часовой стрелке, если смотреть с направления, откуда частицы прилетели (это направление определяется знаком зарядов). И поэтому совокупный эффект для всего облака в результате будет выглядеть, как на рис. 2.
) и отклонить траекторию из этой плоскости. Траектория каждой частицы будет отклоняться в одну сторону, например вправо, по часовой стрелке, если смотреть с направления, откуда частицы прилетели (это направление определяется знаком зарядов). И поэтому совокупный эффект для всего облака в результате будет выглядеть, как на рис. 2.
Подчеркнем, что облако после пролета мимо монополя, конечно, начнет не только вращаться, но и расширяться, поскольку траектории отдельных частиц больше не параллельны друг другу. Но такое расширение, вызванное силовым возмущением, будет и для электрических, и для гравитационных сил. Особенность же взаимодействия в паре «монополь + заряд» именно в новом эффекте, во вращении. Пока расширение облака не слишком заметно, можно сказать, что пролет сквозь монополь просто передал облаку некий механический вращательный момент. А возникает он именно потому, что в паре «заряд + монополь» силы действуют «вбок», в не «вдоль».
Послесловие
Задача о рассеянии заряда на магнитном монополе довольно богата. Ее можно рассматривать на разных уровнях строгости и каждый раз находить занятные эффекты. В этой задаче сделан только первый шаг — выяснена общая картина рассеяния. Следующий шаг, который читатель может сделать самостоятельно, — оценить по порядку величины угол отклонения каждой частицы, по-прежнему считая, что этот угол маленький. Можно также оценить величину приобретенного облаком вращательного момента импульса; ответ, кстати, окажется на удивление простым.

Рис. 5. Магнитное поле на конце длинного и тонкого обычного магнита напоминает поле от монополя, а значит, оно тоже способно закручивать пролетающие заряженные частицы. Физики уже смогли использовать это свойство для получения закрученных электронных волн. Изображение из статьи A. Béché et al., 2013. Magnetic monopole field exposed by electrons
Следующий шаг — это решение той же задачи, но без предположения о малых углах отклонения. Тут траектория может не только сильно отклоняться вбок, но и закручиваться в этакую спираль переменного шага. Более того, у такой сложной траектории есть одна особенность: она полностью лежит на поверхности некоторого конуса, в вершине которого находится монополь. Такое удивительное свойство тоже можно вывести из законов механики тел, которые взаимодействуют через силу Лоренца.
Это всё касалось рассеяния классических частиц. Но такую же задачу можно сформулировать и в рамках квантовой механики: скажем, как будет рассеиваться электронная волна, если она налетит на магнитный монополь? Тут возникает целый букет новых тонкостей, связанных с описанием как самого магнитного монополя, так и движения электрона в его поле. Но качественно результат будет примерно такой же, как и в нашей задаче: электронная волна после пролета закрутится.
Эта тенденция закручиваться после прохождения сквозь монополь уже экспериментально используется для создания закрученных электронов (рис. 5). Конечно монополь тут не настоящий, а приблизительный — просто магнитное поле вблизи конца длинного и тонкого обычного магнита выглядит очень похоже на поле монополя. Но метод всё равно работает. Аналогичный эффект физики уже давно используют в экспериментах по поиску природных монополей. Только в этом случае не электроны налетают на монополь, а сам монополь должен пролететь сквозь сверхпроводящее колечко. Тогда при своем пролете он «закрутит» электронную плотность в сверхпроводнике, то есть наведет в колечке незатухающий ток, который можно будет зарегистрировать. Такие эксперименты действительно ведутся, но до сих пор никакого достоверного сигнала физики не увидели.
Так что можно с полным правом сказать, что в нашей задаче на качественном уровне схвачен эффект, который уже используется в современной экспериментальной физике.
Последние задачи














Рис. 1. Магнитное поле от монополя напоминает электрическое поле от неподвижного электрического заряда: линии поля радиально расходятся от заряда, а его напряженность падает по закону обратных квадратов. Здесь q и qm — электрический и магнитный заряды соответственно