Северное сияние
Задача
Движение заряженных частиц в электромагнитных полях часто имеет очень сложный характер. Но в некоторых случаях, зная простые законы сохранения, его получается достаточно легко охарактеризовать.
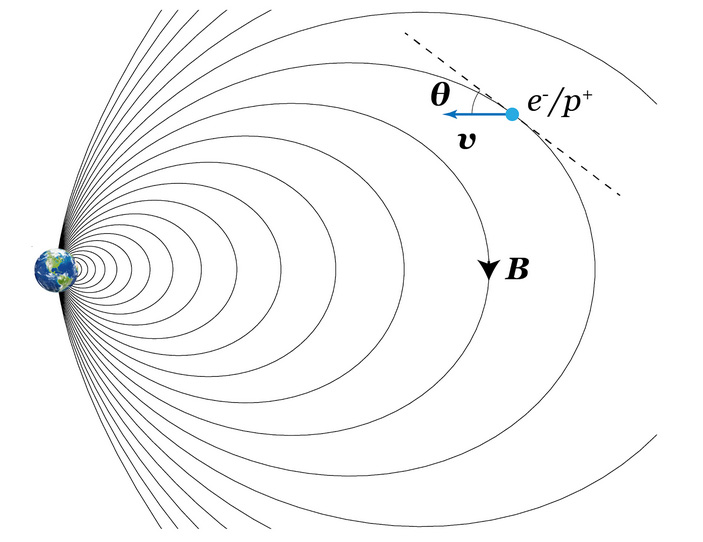
Представим заряженную частицу солнечного ветра — протон или электрон, — который каким-то образом проник в магнитосферу Земли. Для простоты будем считать, что магнитосфера Земли стационарна и имеет форму, показанную на рис. 1.
Величина магнитного поля на расстоянии r от центра Земли задается формулой
\[B(r) = B_0\left(\dfrac{r}{R_0}\right)^{-3},\]где \(R_0\) — радиус Земли, а \(B_0\) — величина напряженности магнитного поля на поверхности Земли (примерно 1 Гаусс).
Также для простоты будем считать, что кинетическая энергия частиц во много раз превосходит их потенциальную энергию в поле тяжести Земли (проверьте это, что это и правда так!).
Чтобы понять, как такая частица будет двигаться в магнитосфере Земли, достаточно знать один простой закон — закон сохранения так называемого первого адиабатического инварианта. Он утверждает, что в стационарном (или достаточно медленно меняющемся) магнитном поле сохраняется величина
\[\mu = \frac{v_{\perp}^2}{B}.\]Здесь \(v_{\perp}\) — компонента скорости частицы, перпендикулярная магнитному полю, a \(B\) — локальная напряженность магнитного поля, которое «чувствует» частица.
Вспомнив, как ведет себя заряженная частица в однородном магнитном поле (см., например, задачи Уровни Ландау и Куда дрейфуют частицы?), попытайтесь описать, что будет происходить с частицей в магнитосфере Земли.
При каком условии частица упадет на поверхность Земли? Заряженные частицы в магнитосфере Земли могут излучать фотоны — при достаточной мощности этого излучения мы видим северное сияние. Объясните, почему северное сияние наблюдается лишь в достаточно высоких широтах.
Подсказка 1
Помимо сохранения адиабатического инварианта \(\mu\) сохраняется и энергия частицы. Причем, так как кинетическая энергия во много раз превосходит потенциальную, последней можно пренебречь.
Подсказка 2
По мере приближения частицы к Земле, величина магнитного поля будет усиливаться. Что будет происходить с компонентами скорости, при условии, что и кинетическая энергия, и первый адиабатический инвариант сохраняются?
Решение
Во-первых, следует заметить, что характерная скорость частиц солнечного ветра, попадающих в магнитосферу Земли, имеет порядок сотен км/с. Это в 10 раз больше, чем первая или вторая космическая скорости Земли (космическая скорость как раз соответствует примерному равенству кинетической и гравитационной энергий). Следовательно, на довольно большом расстоянии от поверхности Земли, гравитационная потенциальная энергия этих частиц пренебрежимо мала по сравнению с кинетической. Это означает, что полная скорость частицы должна сохраняться, так как сохраняется полная энергия, примерно равная ее кинетической.
Выразим обе компоненты скорости (параллельную и перпендикулярную к магнитному полю) через угол \(\theta\) (см. рис. 1):
\[v_{||} = v \cos{\theta},~~\text{и}~v_{\perp} = v\sin{\theta}.\]Закон сохранения первого адиабатического инварианта, который также называется магнитным моментом частицы, запишется следующим образом:
\[\mu = \frac{v_{\perp}^2}{B} = v^2\frac{\sin^2{\theta}}{B}=\textrm{const},\]а следовательно, \(\sin^2{\theta}\propto B\) (так как \(v=\textrm{const}\)). То есть как бы сложно частица не двигалась в этом поле, законы сохранения энергии и магнитного момента требуют, чтобы квадрат синуса угла наклона к магнитному полю был пропорционален величине магнитного поля. Иными словами, если по мере движения частицы, величина магнитного поля увеличивается, то угол \(\theta\) также должен увеличиваться.
Чтобы лучше понять, как частица будет двигаться в таком поле, сначала разберем более простой пример: движение частицы в однородном магнитном поле. Как, возможно, вы помните из школьной физики, сила Лоренца, действующая со стороны магнитного поля на движущуюся заряженную частицу, всегда действует перпендикулярно скорости. Следовательно, если скорость частицы перпендикулярна полю (рис. 2, слева), сила Лоренца будет создавать центростремительное ускорение, а частица при этом будет вращаться по окружности (Ларморовская окружность). Если же у частицы есть компонента, параллельная полю (рис. 2, справа), то частица будет по-прежнему вращаться по Ларморовской окружности, но еще и двигаясь с постоянной скоростью вдоль поля, описывая винтовую траекторию.

Рис. 2. Движение частицы в однородном магнитном поле: слева — скорость частицы направлена перпендикулярно полю, справа — скорость имеет компоненту, параллельную полю
В магнитном поле Земли движение частицы устроено похоже, с той лишь разницей, что по мере движения вдоль поля величина магнитного поля усиливается. Как мы выяснили выше, \(\sin^2{\theta}\propto B\), и из-за усиливающегося магнитного поля, синус угла (а значит — и сам угол) должен расти. Получается, что по мере движения, частица будет вращаться (благодаря составляющей скорости \(v_\perp = v \sin{\theta}\)) и двигаться вдоль поля (благодаря составляющей \(v_{||} = v \cos{\theta}\)). Угол между направлением движения и силовыми линиями поля при этом будет расти, а скорость вдоль поля, \(v_{||}\), падать. Но \(\sin{\theta}\) имеет максимум при \(\theta = 90^\circ\). Когда угол вырастет до этого значения, скорость вдоль поля у частицы станет равна нулю, и частица «отразится», улетев в противоположном направлении, как это показано на рис. 3.

Рис. 3. Отражение частицы в магнитосфере Земли (слева — при большом \(\theta_1\), справа — при малом)
Чтобы найти на каком расстоянии от поверхности происходит это отражение, достаточно учесть, что в момент отражения \(\sin{\theta'}=1\):
\[ \frac{\sin^2{\theta_1}}{B_1} = \frac{1}{B'},\]где \(\theta_1\) и \(B_1\) — угол и магнитное поле в момент начала движения, а \(B'\) — величина магнитного поля в момент отражения. Отсюда, зная, что \(B=B_0(r/R_0)^-3\), при заданных начальных \(\theta_1\) и \(B_1\) (или \(r_1\) — высоту с которой стартовала частица) можно найти \(r'\) — высоту, где произошло отражение:
\[r' = r_1 \sin^{2/3}{\theta_1}.\]Из этой формулы видно, что чем меньше \(\theta_1\), то есть чем «параллельнее» к полю движется частица вначале, тем ближе к Земле она может проникнуть. В предельном случае, конечно, когда \(r' = R_0\) (то есть когда высота сравнима с радиусом Земли), можно считать, что частица солнечного ветра достигла Земли. При этом есть критический угол \(\theta_{\rm кр}\): если угол между скоростью частиц и магнитным полем изначально больше критического, то частицы отразятся раньше, чем достигнут поверхность Земли (см. рис. 4).
Послесловие
Давайте представим упрощенную ситуацию, когда вместо поверхности Земли есть некоторая плоская поверхность с петлеобразным магнитным полем (как показано на рис. 4). В таком случае, по аналогии с нашей задачей, частицы, которые стартуют с самого центра петли под углом \(\theta\) к магнитному полю, будут долетать до поверхности, только если \(\theta < \theta_{\rm кр}\). Частицы с большим углом наклона будут вечно болтаться в таком магнитном поле, отражаясь на некоторой высоте и никогда не достигая поверхности.
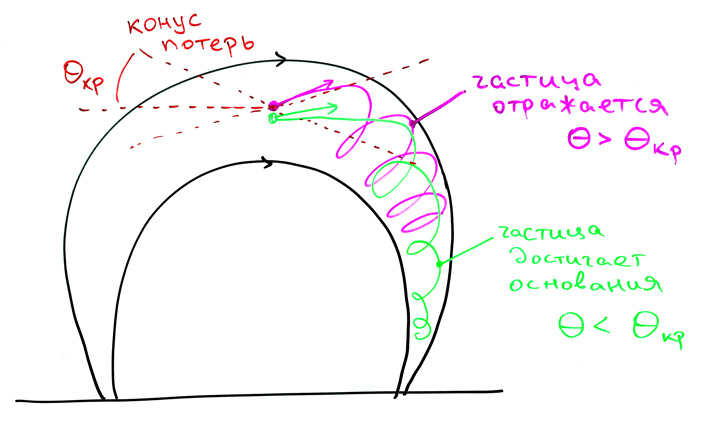
Рис 4. Конус потерь в упрощенной конфигурации магнитного поля
Область углов \(\theta < \theta_{\rm кр}\) называется в физике плазмы конусом потерь: все частицы, скорость которых находится в этом конусе, будут «утекать» из системы.

Рис. 5. «Магнитное зеркало» для плазмы. Рисунок с сайта farside.ph.utexas.edu
Понятие конуса потерь — принципиальная концепция в теории магнитного удержания плазмы. В середине прошлого века с помощью таких «магнитных зеркал» инженеры пытались добиться удержания сверхгорячей плазмы для получения стабильного термоядерного синтеза. Однако, именно из-за наличия конуса потерь, то есть из-за наличия частиц, которые «убегают» из такой ловушки под определенным углом, задача оказалась гораздо сложнее. От такой линейной конфигурации вскоре отказались, заменив ее на тороидальные токамаки.
Вернемся, однако, к магнитосфере Земли и северному сиянию. Во-первых, давайте поймем, каким образом частицы солнечного ветра проникают в нашу магнитосферу и почему, собственно, происходит северное сияние. Частицы солнечного ветра — в основном электроны и протоны — летят вдоль силовых линий магнитного поля Солнца к нам со скоростями в несколько сотен км/с. При этом напрямую проникнуть в магнитосферу Земли они не способны: вспомните, что частица в магнитном поле движется по окружности с некоторым радиусом, который в данном случае мал по сравнению с размерами системы. То есть частицы «не любят» пересекать магнитные силовые линии — они могут свободно двигаться только вдоль; иногда говорят даже о «вмороженности» плазмы в магнитные силовые линии.
При столкновении солнечного ветра с магнитосферой Земли противоположно направленные магнитные поля пересоединяются (рис. 6, кадр 2), после чего магнитные силовые линии замыкаются обратно с противоположной стороны Земли (рис. 6, кадры 3 и 4). С обратной стороны силовые линии уже земной магнитосферы, которые несут с собой энергичные частицы солнечного ветра, снова пересоединяются, замкнувшись обратно. Теперь заряженные частицы солнечного ветра, вмороженные в магнитные линии уже «официально» находятся внутри земной магнитосферы.
Двигаясь вдоль силовых линий, энергичные частицы могут ионизировать молекулы и атомы газов в верхних слоях атмосферы, которые в результате излучают. На самом деле, сияние бывает и в южном полушарии (рис. 7), но по историческим причинам в русском языке оно называется именно «северным». При этом широта определяется тем, с какой именно силовой линии частицы прилетели в атмосферу (рис. 6, кадры 5 и 6). Магнитная силовая линия Земли, которая соединилась с силовыми линиями солнечного ветра, исходила не прямо с магнитного полюса, а чуть ближе к экватору. Из-за этого сияние чаще всего видно на самых северных или самых южных широтах. При этом, если сила солнечного ветра достаточно большая, то пересоединиться могут более «глубокие» силовые линии магнитного поля Земли, из-за чего северное сияние можно будет наблюдать на более низких широтах.
-
Всегда смущали эти линии...
Думал, они условность, поле едино, однородно, плавно усиливается, уплотняется к центру.
А тут не только линии, но они еще и рвутся именно как слои, как шкурка слазит с банана.
поле ведет себя не как однородная, неслоистая, вроде капли масла в воде, штука...
Не, никогда мне этого не понять.
Последние задачи



















Рис. 1. Заряженная частица, движущаяся в магнитосфере Земли