Куда дрейфуют частицы?

Начните с частицы, которая влетает в такое поле где-то в верхней его половине со скоростью, направленной вдоль оси x. Раз поле направлено на нас, траектория будет заворачивать вниз, к разделительной линии. Но там поле ослабевает, и траектория там будет поворачиваться менее круто. Интуитивно понятно, что дальнейшая судьба траектории зависит от того, пересечет частица разделительную линию или нет, — ведь в поле, направленном от нас, она будет поворачиваться в другую сторону. Попробуйте нарисовать разные варианты траектории в зависимости от того, пересекла траектория среднюю линию или нет. Не упустите из виду и зеркальную симметрию этой задачи.

Если вам трудно рисовать плавно распрямляющуюся траекторию, начните с варианта попроще, как на рис. 3. Здесь тоже есть разделительная линия, выше которой поле направлено на нас, а ниже — от нас, но только в каждой половине поле однородно. Поведение частицы в однородном поле мы знаем, поэтому будет нетрудно нарисовать траекторию частицы таком поле.

Рис. 3. Упрощенная задача с двумя областями однородного поля

Этот прием можно использовать и для случая, когда частица не пересекает разделительную линию. Надо лишь нарисовать две области, в которых поле направлено на нас, но имеет разную напряженность.

Если траектория частицы не пересекает разделительную линию, то траектории частиц, запущенных в разных точках, выглядят, как на рис. 4. Метод их рисования прост: траектория закручивается сильнее там, где сильнее поле. Обратите внимание на две вещи. Во-первых, во всех вариантах частица с положительным зарядом дрейфует налево. Это справедливо и выше, и ниже разделительной линии из-за симметрии задачи. Во-вторых, чем дальше частица от разделительной линии, тем медленнее она дрейфует. Далеко от средней линии поле очень сильно, поэтому радиус окружности маленький, а значит, частица не улетает далеко и «прощупывает» области с практически одинаковым полем. Ее траектория — почти что замкнутая окружность, и она лишь чуть-чуть смещается вбок на каждом обороте. Напротив, если траектория проходит близко к средней линии, то радиус кривизны велик, и частица то улетает достаточно далеко, то приближается очень близко к середине. Ее траектория сильно отличается от окружности, поэтому на каждом цикле она сдвигается вбок очень сильно.

Рис. 4. Движение частицы с положительным зарядом в том случае, если ее траектория не пересекает разделительную линию

В случае, когда траектория пересекает среднюю линию, появляется новая возможность: частица может дрейфовать как налево, так и направо (рис. 5). Всё зависит от того, в каком именно месте пересекается средняя линия относительно верхней точки траектории.

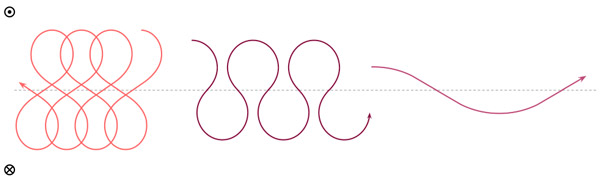
Рис. 5. Варианты движения частицы, когда ее траектория пересекает разделительную линию

Описанный в задаче вариант дрейфа частицы в неоднородном магнитном поле называется градиентным дрейфом. Для случая, когда траектория не сильно отличается от окружности (как на рис. 4 вдали от линии), формула для скорости этого дрейфа имеет простой вид:

Здесь  — это градиент модуля магнитного поля, то есть вектор, направленный в ту сторону, в которую поле усиливается. В нашем примере он направлен вверх и вниз прочь от разделительной линии. Видно, что чем больше поле, тем сильнее оно «зажимает» частицу и тем медленнее получается дрейф.

Градиентный дрейф — это лишь одно из множества дрейфовых явлений, которые возникают при движении заряженной частицы в сложных полях. Магнитное поле с искривленными силовыми линиями, скрещенные электрические и магнитные поля, сила тяжести, поля, меняющиеся во времени, — всё это тоже вызывает соответствующий дрейф заряженных частиц. Ну а когда эти эффекты присутствуют одновременно, картина движения частиц может оказаться очень нетривиальной, что придает этой задаче богатство и глубину. Некоторое введение в эту тему можно найти в лекции Движение частиц в магнитном поле, которая читается на кафедре физики плазмы в НГУ.

Чтобы не казалось, будто бы это чисто академическая задача, приведем два реальных физических примера, где эти вопросы играют важнейшую роль. Во-первых, это поведение плазмы в токамаке и других магнитных ловушках, предназначенных для термоядерной энергетики. В них плазму — газ заряженных частиц — запускают в сложное внешнее магнитное поле. Плазма движется, текут токи, они искажают внешнее магнитное поле и, в виде обратной связи, влияют на собственное движение. Разобраться с дрейфом частиц, а значит, и с поведением плазмы в этой ситуации — одна из сложнейших задач, которую предстоит решить на пути к успешной термоядерной энергетике.

Второй пример — космический. Космос — как далекий, так и близкий — наполнен магнитными полями и заряженными частицами. Можно сказать, что природа постоянно ставит многочисленные эксперименты по поведению заряженных частиц в магнитных полях самых разных конфигураций. Магнитные поля с дрейфующими в них частицами присутствуют и вблизи Земли. Радиационные пояса ван Аллена, опоясывающие планету, — это надолго застрявшие в дрейфе заряженные частицы. Они создают токи вокруг Земли, порождают полярные сияния, а также создают проблемы для пилотируемой космонавтики.