На всю катушку

Жизнь станет проще, если вспомнить (или сообразить), что такое мгновенная ось вращения. Хотя вообще у задачи множество вариантов решения.

Сначала пара слов в продолжение подсказки. Скорость нити U мы определяем относительно неподвижных объектов. В нашем случае такой объект только один — это поверхность, по которой катится катушка. И относительно этой поверхности у катушки всегда есть одна точка, скорость которой равна нулю: точка С — место ее сцепления с поверхностью. Да, эти точки каждый раз разные, но в любой момент времени (если, скажем, сфотографировать) такая точка одна. При условии, конечно, что и катушка, и стол абсолютно твердые, то есть не подвержены деформации. Эту точку и называют мгновенной осью вращения, МОВ (или мгновенным центром скоростей, МЦС).

Вернемся к задаче. Разных решений тут действительно множество и чуть ниже мы некоторые из них разберем, но начнем с применения идеи мгновенной оси вращения.

Разберемся сначала со случаем, в котором нить горизонтальна.

Введем обозначения: V — скорость оси катушки, ɑ — угол нити к горизонту, U — скорость нити, R и r — радиусы внешней и внутренней части катушки, соответственно.

Итак, как мы сказали, точка С — единственная неподвижная точка катушки относительно поверхности в произвольный момент времени. Если при этом тянуть связанную с катушкой нить, это, очевидно, будет вызывать вращение катушки вокруг этой точки как вокруг оси — ведь других неподвижных точек нет. Поэтому ее движение в каждый момент времени хорошо описывается, как вращение вокруг этой мгновенной оси (в «следующий» момент катушка «немного» поворачивается, эта точка чуть-чуть смещается по ее ободу и т. д.). А значит, у катушки есть своя угловая скорость. Обозначим ее, как водится, ω (рис. 3).

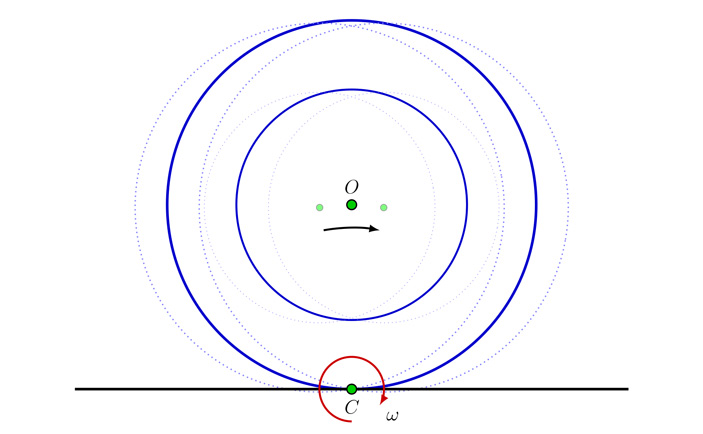
Рис. 3.

Условие, что движение происходит без проскальзывания, позволяет воспользоваться уравнением связи между угловой и линейной скоростью:

где \(V_x\) — линейная скорость произвольной точки X на катушке, а \(R_x\) — расстояние от оси вращения С до этой точки (рис. 4).

Рис. 4.

Если обозначить буквой A самую верхнюю точку обода катушки, то для точек, лежащих на отрезке АС, значение линейной скорости будет меняться от \(V_A=\omega\cdot2R\) до нуля для мгновенного центра скоростей С (рис. 5).

Рис. 5.

Кстати, если мысленно продолжить отрезок AC ниже поверхности (за точку C), то окажется, что векторы скоростей поменяют направление (рис. 6). Это означает, что если, например, вместо катушки у нас катящийся по направляющим шар (часть которого оказывается ниже направляющих) или колеса поезда (на которых имеются выступающие части, удерживающие поезд на рельсах — так называемые реборды), то в них в каждый момент времени будут области, которые движутся «навстречу» самому объекту (относительно направляющих/рельсов). Именно точки на ребордах — это ответ на популярный шуточный вопрос о наличии в поезде частей, которые едут в обратном направлении.

Рис. 6.

Вернемся к задаче.

Ось катушки О находится на расстоянии R от мгновенной оси вращения С, поэтому ее линейная скорость равна \(V_O=\omega R\). Скорость точки B (она расположена на внутренней части катушки в месте отрыва нити) будет, в силу нерастяжимости нити, равна U, что дает равенство \(U=\omega(R-r)\), из которого выражается угловая скорость катушки:

Значит, линейную скорость оси O можно записать так:

Мы рассчитали значение скорости оси катушки относительно земли. Но расчет делался для одного мгновения, в которое данная точка С была неподвижна и могла послужить осью вращения. Будет ли этот результат справедлив для постоянного движения? Как мы уже говорили, такая ось С в каждый момент времени новая. Но она ничем не отличается от предыдущей. Для любой из мгновенных осей С, взятых подряд, мы можем рассчитать значение линейной скорости оси О и получить тот же ответ. Это означает, что \(V_O\) постоянна в любой точке траектории и в течение всего качения, и соответствует реальному движению (и это подтверждается другими способами решения и — главное — экспериментами, практикой).

Итак, мы получили ответ на первый вопрос. Давайте посмотрим на него внимательнее и предупредим мышей о возможных последствиях такого результата.

R, очевидно, больше, чем \((R-r)\), а значит, дробь \(\frac{R}{R-r}\) всегда больше единицы. Следовательно, скорость \(V_O\), с которой катится катушка по полу, всегда больше скорости U, с которой ее тянут за нитку. То есть катушка всегда нагоняет того, кто тянет нить!

Чем больше внутренний радиус r (то есть чем ближе он по значению к R), тем больше будет скорость катушки и тем быстрее она будет нагонять волшебного мула! И для того, чтобы не ушибить редкое и чувствительное животное, мышкам надо бы хорошо рассчитать длину свободного конца нитки, чтобы правосудие в лице катушки не настигло их прежде, чем они достигнут места назначения.

Когда катушка делает один полный оборот, она проезжает по земле расстояние, равное длине ее окружности, то есть \(2\pi R\). За это же время барабан, сделавший, очевидно, также один оборот, намотает участок нити длины \(2\pi r\). То есть расстояние между катушкой и мулом сокращается на величину \(2\pi r\) за каждый участок пути длиной \(2\pi R\), и это не зависит от скорости мула. Если расстояние до мышиного цирка принять за L, то число оборотов, которое совершит катушка по пути до своего нового места жительства, будет равно \(\frac{L}{2\pi R}\), а длина нити, намотанная за время пути на барабан, — \(\frac{L}{2\pi R}\cdot2\pi r=L\frac rR\) (при условии, конечно, что цирк не очень далеко и радиус r не успеет измениться из-за наматывания нити). Следовательно, для безопасной транспортировки понадобится нитка, равная \(\frac rR\) расстояния до цирка.

Теперь посмотрим, что будет, когда нить тянут под углом α к горизонту.

Нужно выбрать точку, движение которой удобно для отыскания угловой скорости. Точка В здесь, очевидно, — не слишком удачный выбор, так как направление ее движения будет перпендикулярно отрезку СВ (ее радиусу относительно мгновенной оси вращения) и сложно поддается описанию. А вот точка D, лежащая на «продолжении» нити и такая, что угол CDB прямой (другими словами — проекция точки C на линию нити), то ее скорость вокруг МОВ будет совпадать с U и по модулю, и по направлению (рис. 7). Следовательно, скорость точки D как линейная при круговом движении вокруг оси С равна \(V_D=\omega\cdot CD=U\).

Рис. 7.

Теперь немного геометрии. Отрезок ОВ, равный радиусу r, перпендикулярен нити (как радиус к касательной окружности). Достроим на сторонах DС и ВD прямоугольник BECD. Заметим, что углы COE и α равны (как углы со взаимно перпендикулярными сторонами). Из треугольника ОCE следует, что \(OE=OC\cdot\cos\alpha=R\cdot\cos\alpha\), а \(BE=OE-OB=R\cdot\cos\alpha-r\). Далее, \(DC=BE\), как противоположные стороны прямоугольника, а линейная скорость точки D, как мы помним, равна U.

Откуда легко найти, что угловая скорость катушки вокруг МОВ равна \(\omega=\frac{U}{R\cdot\cos\alpha-r}\), а искомая скорость оси —

Заметим, что знак скорости будет меняться в зависимости от значения угла α — когда его косинус станет меньше отношения радиусов (это произойдет при достаточно большом угле), катушка начнет катиться в сторону, противоположную движению нити (речь о диапазоне значений α от 0 до 90° — при углах, больших 90°, задача переходит в другую, где нить выходит сверху барабана; в этом случае скорость оси всегда будет сонаправлена горизонтальной составляющей скорости нити).

Какой же вывод следует для мышек из всех этих замечательных открытий?

Чтобы катушка покатилась за ними к цирку, им следует тянуть ее за нить либо горизонтально, либо под углом, для которого верно неравенство \(\cos\alpha<\frac rR\). Как определить его на глаз, мы поговорим в послесловии.

Для начала давайте для горизонтальной нити получим значение скорости оси \(V_O\), как и обещали, другим способом — через сложение скоростей.

Заметим, что найти скорость оси можно, рассматривая качение катушки как сумму двух независимых движений: поступательного и вращательного, но уже вокруг оси катушки О.

Поступательное движение охарактеризуем скоростью \(V_p\), она будет одинаковой для всех точек катушки, а вращательное — угловой скоростью \(\omega_O\). Тогда скорость произвольной точки X катушки складывается из линейной составляющей ее вращательного движения \(V_X=\omega_OR_X\) и поступательного движения всей катушки со скоростью \(V_p\).

Рис. 8.

В частности, скорость точки С равна \(V_C=\omega_OR\), а поскольку точка C покоится относительно поверхности верно равенство \(V_C+V_p=0\). То есть эти скорости противоположно направлены и равны по модулю, откуда находим, что \(\omega_O=\frac{V_p}{R}\).

Скорость точки В складывается из противоположно направленных \(V_p\) и \(\omega_Or\), в сумме дающих скорость нити U: \(U=V_p-\omega_Or\).

Скорость оси О не зависит от вращательного движения и равна только скорости поступательного, которую можно выразить из двух предыдущих соотношений: \(V_O=\frac{UR}{R-r}\). Этот же результат в решении мы получили, используя мгновенную ось вращения. Надо заметить, что эта формула — частный случай ответа для ситуации, когда нить направлена под углом α к горизонту: ведь здесь \(\alpha=0^\circ\), а значит, \(\cos\alpha=1\), — поэтому, в принципе, эти две ситуации не обязательно разделять.

Мы решали задачу средствами кинематики, то есть без учета причин, вызвавших движение. Понятно, что в реальной жизни нить вытягивается с определенной силой F, а катушка обладает собственной массой m и, следовательно, моментом инерции \(I=\gamma mR^2\), где γ — некий числовой коэффициент. Однако решение и при этих условиях дало бы нам тот же самый угол направления нити, под которым происходит смена направления ускорения: угол, под которым продолжение нити проходит через мгновенную ось вращения (как раз этому условию отвечает равенство \(\cos\alpha=\frac rR\)).

Рис. 9.

Если учесть все действующие на катушку силы, то уравнение ее движения в проекции на горизонтальную ось будет таким:

Уравнение вращательного движения: \(I\beta=-Fr+ F_{\mathrm{тр}}R\), где \(\beta\) — угловое ускорение, которое в силу того, что катушка движется без проскальзывания, связано с ее линейным ускорением равенством \(a=\beta R\).

Откуда линейное ускорение оси катушки получается таким:

Обратите внимание, что знак ускорения меняется при том же самом значении угла.

На самом деле, этот факт легко установить и безо всяких вычислений, если вновь обратиться к мгновенной оси вращения, а также вспомнить про момент силы (который равен векторному произведению радиус-вектора, идущего от центра вращения к точке приложения силы, и самой силы). Как видно из рис. 10, направление момента силы (которое напомним, определяется по правилу буравчика) разное для случаев \(\cos\alpha>\frac rR\) и \(\cos\alpha<\frac rR\), поскольку в первом случае поворот от радиус-вектора \(\vec R_D\) к вектору силы \(\vec F_D\) идет в одном направлении (по часовой стрелке), а во втором случае — в противоположном.

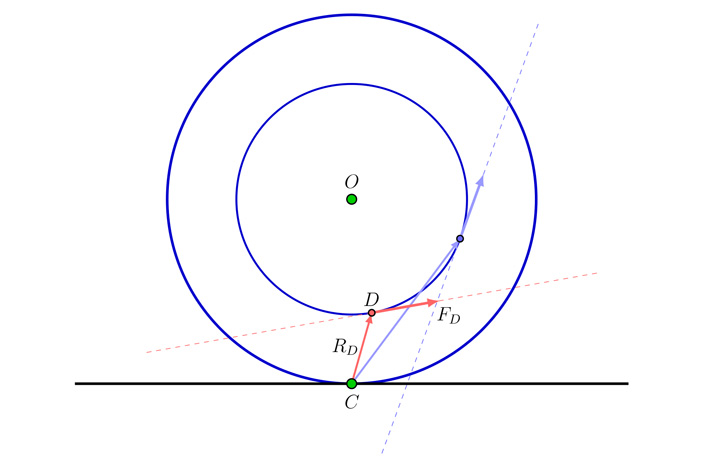
Рис. 10.

Если волшебный мул принялся бы тянуть нитку именно под этим «критическим» углом α, для которого \(\cos\alpha=\frac rR\), его усилия пропали бы втуне: катушка не сдвинулась бы с места. Впрочем, если бы он был достаточно силен, чтобы нарушить условие «движение происходит без проскальзывания», то смог бы добиться того, что катушка вращалась бы на одном месте. Но эта дорога не ведет к цирку. То есть катушку нужно тянуть так, чтобы продолжение нити проходило над точкой С — местом соприкосновения катушки и поверхности. И тогда она точно покатится в цирк.

После всего вышесказанного можно сходу ответить, например, на такой вопрос: «как лучше вытаскивать застрявшую телегу: толкая саму телегу или верхнюю часть колеса?»

Рис. 11.

Телега связана с колесами через оси, так что, толкая ее, мы создаем момент силы относительно мгновенной оси вращения (которая точно так же находится в месте касания колесом земли), равный \(M_1=[\vec r\times \vec F]\), а проворачивая верхнюю часть обода — \(M_2=[\vec R\times \vec F]\), что, очевидно, в два раза больше. Другими словами, можно сказать, что вдвое больше плечо силы (или рычаг). А значит, толкать лучше верхнюю часть обода (правда, остается еще вопрос удобства этого процесса).

Концепция мгновенной оси вращения хороша не только для быстрого решения бытовых вопросов вроде катушки или телеги (если у кого-то в быту возникают проблемы с телегами), но и для расчетов кривошипно-шатунных механизмов в механике, нагрузки на суставы в биофизике, движения планет и спутников в небесной механике и т. д., везде значительно упрощая модель и облегчая расчеты.

В заключение предлагаем посмотреть на эксперимент с катушкой, проведенный в программе «Галилео» неподражаемым Александром Пушным.