Точка Торричелли и сети Штейнера (окончание)

Владимир Протасов
«Квантик» №12, 2021

Начало — в «Квантике» №10 и №11, 2022.

Для построения нам понадобится одно несложное, но очень важное утверждение. Пусть мы соединили города допустимой сетью дорог. Город будем называть тупиковым или просто тупиком, если из него выходит только одна дорога. Заметим, что тупиковых перекрёстков не бывает.

Вспомогательный факт: в любой допустимой сети найдётся либо город, из которого идёт дорога в  тупик, либо перекрёсток, из которого выходят две дороги к тупикам. (При этом, конечно, как из города, так и из перекрёстка могут выходить и другие дороги.)

Доказательство простое. Среди всех путей в сети выберем путь, в котором наибольшее число дорог. Он не замкнутый (таких не бывает), поэтому у него есть два конца. Возьмём любой конец. Это тупиковый город. Он соединён единственной дорогой с некоторой вершиной A. Если A — город, то из него выходит дорога в тупиковый город. Если же A — перекрёсток, то из него выходит ещё одна дорога в тупиковый город, иначе можно сделать путь из большего числа дорог.

Построение кратчайших сетей

Сеть Штейнера будем строить так: найдем все допустимые сети, а из них выберем кратчайшую. Она и  будет сетью Штейнера. Построение допустимой сети для k городов мы сведём к построению для k − 1 городов. Так, постепенно спускаясь, дойдём до k = 2. А для двух городов допустимая сеть состоит из одной дороги — отрезка между двумя городами.

Идея построения. Пусть допустимая сеть для k городов уже построена.

Если в ней есть город, из которого выходит дорога в тупик, то уберём эту дорогу вместе с тупиковым городом. Оставшаяся сеть тоже будет допустимой сетью, но уже для k − 1 городов.

Рис. 11

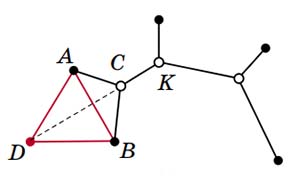
Если же в нашей сети есть перекрёсток (обозначим его C), из которого выходят две дороги к тупиковым городам (A и B), то поступим так. Построим на стороне AB треугольника ABC во внешнюю сторону равносторонний треугольник ABD. Теперь уберём города A и B (вместе с дорогами, которые к  ним ведут), заменив их одним новым городом  D. Уберём вершину C и соединим два отрезка CD и CK в одну дорогу KD (рис. 11). Почему так можно сделать? Потому что QACB = 120°, и по теореме 1 угол DCA равен 60°. Поэтому отрезки CD и CK лежат на одной прямой. Эти отрезки составляют новую дорогу от точки K до тупикового города D. Мы снова получим допустимую сеть для k − 1 городов (k − 2 оставшихся городов плюс город D). Причём длина допустимой сети останется прежней, потому что CD = CA + CB (теорема 1), то есть новая дорога CD компенсирует две убранные (CD = CA + CB).

Так, уменьшая шаг за шагом число городов, придём к двум городам, а для них допустимая сеть — отрезок. Двигаясь обратно, мы можем, начиная с двух городов, восстановить всю сеть.

Теперь начинаем построение сетей. Будем строить их двумя способами, и в результате получим все допустимые сети, связывающие k городов

• Перебираем все наши города по одному, и для каждого города делаем такую процедуру. Обозначим очередной город через А. Уберём его, и построим допустимую сеть, связывающую оставшиеся k − 1 городов. А теперь соединяем A новой дорогой с любым другим городом B. Проверяем, что AB образует со второй дорогой, выходящей из B, угол, не меньший 120°. Если это так, мы получили допустимую сеть для всех k городов. А если этот угол меньше 120°, надо выбрать другой город вместо B. Так нам нужно перебрать все допустимые сети, связывающие наши k − 1 городов, и для каждой сети — все возможные города В.

• Берём любую пару городов A, B и строим равносторонний треугольник ABD (их два, берём любой). Заменяем A, B одним городом D. Строим допустимую сеть для нового множества из k − 1 городов, для которой город D тупиковый. На единственной дороге, выходящей из города D, найдём точку C, для которой QACB = 120°, и делаем в ней новый перекрёсток. Заменяем дорогу DC двумя дорогами CA и CB. Мы получили допустимую сеть для наших k городов. И так нам нужно перебрать все пары городов A и B. Для каждой пары рассматриваем обе возможности для точки D и в каждом случае перебираем все допустимые сети, для которых город D тупиковый.

Заметим, что точку C найти просто: в силу теоремы 1, угол ACD будет равен 60°. Построим такую точку C на прямой, содержащей дорогу из точки D. И если С попала на саму дорогу, а не на её продолжение — получаем допустимую сеть.

Так мы построим все допустимые сети, и кратчайшая из них — сеть Штейнера.

Примеры сетей Штейнера

Треугольник. После примера с квадратом, когда вроде бы очевидный ответ оказался неверным, мы можем ожидать сюрпризов и от треугольника. Правда ли, что кратчайшая сеть дорог, связывающих три города, — это либо три дороги к единственному перекрёстку (точке Торричелли), либо две стороны, образующие угол не меньше 120° (когда таковой есть)? Применяем наш алгоритм построения сети Штейнера:

Случай 1. Убираем один город (скажем, A). Строим сеть Штейнера двух оставшихся городов — отрезок BC. Теперь возвращаем город A и соединяем его либо с B, либо с C. Пробуем B. Если угол ABC не меньше 120°, то сеть Штейнера найдена — она состоит из дорог AB и BC (рис. 12а). Если нет, то пробуем C. Если угол ACB не меньше 120°, то сеть Штейнера состоит из дорог AC и BC. Если же и это неверно, то переходим ко второму случаю.

Рис. 12

Случай 2. Берём два любых города, скажем A и B. Строим на стороне AB равносторонний треугольник ABD. Убираем A и B и заменяем их городом D. Получили два города: C и D. Их сеть Штейнера  — отрезок  CD. Возвращаем A и B и находим на отрезке CD точку T, для которой QATB = 120°. Получаем точку Торричелли T и сеть Штейнера: дороги TA, TB, TC.

Итак, точка Торpичелли определяет кратчайшую сеть для трёх городов. Здесь обошлось без сенсаций.

Квадрат. Какова кратчайшая система дорог для вершин квадрата? Пока можно точно сказать, что это не две диагонали. Во-первых, есть более короткая сеть (рис. 1). Во-вторых, в перекрёстке не могут сходиться четыре дороги. Будет ли сеть Штейнера иметь два перекрёстка или больше, сейчас узнаем.

Рис. 13

Случай 1. Убираем один город. Из симметрии — неважно какой (пусть снова A). У оставшегося треугольника BCD углы меньше 120°, поэтому у него есть точка Торpичелли T, а его сеть Штейнера состоит из отрезков TB, TC, TD (рис. 13). Теперь мы должны вернуть город A и соединить его с одним из трёх городов, чтобы угол между дорогами получился не меньше 120°. Таких городов нет. Значит, этот случай невозможен.

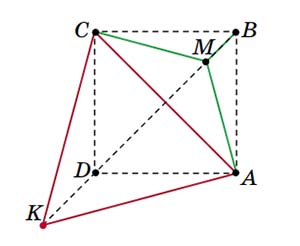
Рис. 14

Случай 2. Убираем два города. Это либо соседние вершины квадрата, либо противоположные. Начнём со второго случая — убрали вершины A и C. Строим равносторонний треугольник ACK и заменяем города A и C городом K. Получились три города на одной прямой: K, B и D. Их сеть Штейнера — дороги BD и DK. Теперь возвращаем точки A и C и делаем на отрезке DB перекрёсток M, для которого QAMC = 120° (рис. 14). Тогда в этом перекрёстке будут сходиться 4 дороги, чего не может быть.

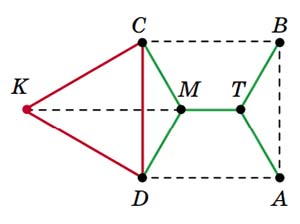
Рис. 15

А теперь предположим, что убрали две соседние вершины квадрата, пусть С и D. Строим равносторонний треугольник CDK и  заменяем C и D городом K. Сеть Штейнера треугольника KАВ — три дороги, соединяющие его вершины с его точкой Торричелли T. Теперь возвращаем С и D и находим на отрезке KТ точку M, для которой QCMD = 120°. Всё, сеть Штейнера построена. У  неё два перекрёстка — в точках T и M (рис. 15). Мы связали вершины квадрата кратчайшей системой дорог. Если сторона квадрата равна 100 км, то длина сети равна 100(\(\sqrt{3}\)+1)=273,2... км. Другие примеры сетей Штейнера — в упражнениях 7–11.

А что в пространстве?

Если есть несколько точек в пространстве и паучок хочет связать их паутиной кратчайшей длины, мы снова получим задачу о кратчайшей системе «дорог». Интересно, что пространственная сеть Штейнера тоже будет обладать свойствами 1, 2, 3. Убедитесь сами, что доказательства мало чем отличаются. Например, если 4 точки расположены в вершинах правильного тетраэдра (то есть в вершинах пирамидки на одном и том же расстоянии друг от друга), то какова будет сеть Штейнера? Кажется, что нужно просто соединить 4 точки с центром тетраэдра. По  аналогии с  равносторонним треугольником: соединяем вершины с центром и получаем сеть Штейнера. Но нет, теперь так не получится. В перекрёстке не могут сходиться четыре дороги! А какая же будет сеть в этом случае? Об этом — упражнение 12.

Напоследок — о мыльных плёнках

Возьмём две параллельные прозрачные доски (например, сделанные из оргстекла), соединённые стержнями. Между досками должен быть зазор. Опустим эту конструкцию в мыльный раствор. А  потом вытащим. Между стержнями образуются плёночные перегородки. Какую фигуру они образуют? Поскольку, как мы знаем, физическая система стремится уменьшить свою потенциальную энергию, общая длина перегородок должна быть минимальна. Естественно предположить, что перегородки образуют сеть Штейнера для «городов» — стержней. Однако, проделав этот эксперимент несколько раз, мы убедимся, что фигуры получатся разные. Как же так? На самом деле, всегда будут получаться допустимые сети (обладающие свойствами 1, 2, 3). Среди них, конечно, будет и сеть Штейнера, но могут получиться и другие. Дело в том, что мыльные плёнки примут положение, как скажут математики, локального минимума длины. Не будем углубляться в этот вопрос, скажем только, что допустимым сетям как раз соответствуют локальные минимумы. Для трёх точек допустимая сеть только одна, поэтому и мыльные плёнки всегда будут принимать одну и ту же форму. То же  (с точностью до симметрии) — для квадрата (рис. 16).

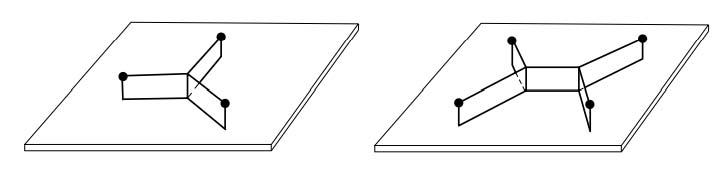
Рис. 16

Упражнение 6. Какие из сетей на рисунке 17 допустимые?

Рис. 17

Упражнение 7. Четыре точки расположены в вершинах трапеции. Придумайте такую трапецию, чтобы сеть Штейнера состояла из трёх отрезков.

Упражнение 8. Постройте сеть Штейнера для четырёх вершин прямоугольника 3×4.

Упражнение 9. Даны 6 точек: вершины прямоугольника 1×2 и середины двух его больших сторон. Постройте несколько допустимых сетей для этих точек. Чем больше — тем лучше.

Упражнение 10. Как может выглядеть сеть Штейнера для вершин правильного пятиугольника? Предложите несколько вариантов. Указание. Можете провести эксперимент с мыльными плёнками, но можно и без этого.

Упражнение 11. Две деревни расположены с одной стороны от прямолинейной дороги на расстоянии 10 км друг от друга и на равном расстоянии 5 км от реки. Где нужно поставить магазин, чтобы сумма расстояний от него до деревень и до дороги была наименьшей? Указание. Может помочь симметрия относительно дороги.

Упражнение 12. Как вы думаете, как выглядит сеть Штейнера для вершин правильного тетраэдра?

Художник Алексей Вайнер