Правильный двенадцатиугольник и его диагонали

Николай Авилов
«Квантик» №2, 2025

Художник Татьяна Долгая

Австрийцы высоко чтут память композитора Йозефа Хауэра потому, что он разработал свою 12-тоновую систему создания музыкальных композиций. Именно поэтому на австрийской почтовой марке 1983 года, выпущенной к столетию со дня рождения композитора, изображён его портрет на фоне правильного двенадцатиугольника с проведёнными диагоналями.

Хауэр к математике имеет косвенное отношение, а вот двенадцатиугольник с его диагоналями (рис. 1) — любопытный объект для интересующихся математикой¹.

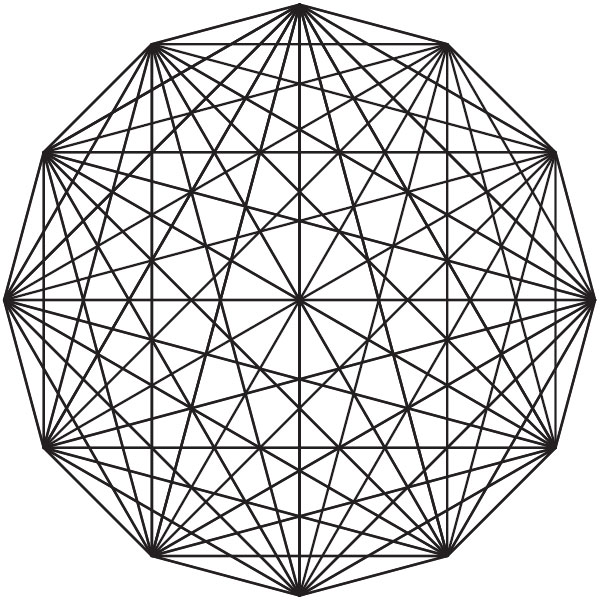
Рис. 1

Как же построить правильный двенадцатиугольник, используя классические инструменты: циркуль и линейку? Существует несколько приёмов, но мы рассмотрим, пожалуй, самый короткий.

Вначале построим две взаимно перпендикулярные прямые, пересекающиеся в точке О, затем с центром в этой точке построим окружность произвольного радиуса (рис. 2).

Рис. 2

Точки пересечения А₁, А₄, А₇ и А₁₀ окружности с прямыми — это четыре вершины двенадцати угольника. Построим четыре окружности того же радиуса с центрами в точках А₁, А₄, А₇ и А₁₀ и найдём ещё восемь вершин двенадцатиугольника (рис. 3).

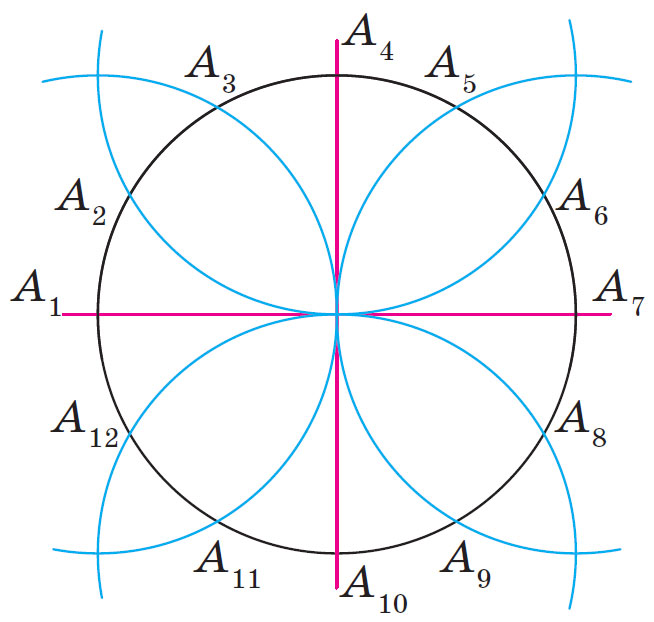
Рис. 3

Осталось соединить вершины по порядку и провести диагонали полученного правильного двенадцатиугольника А₁... А₁₂ (рис. 4).

Рис. 4

Сразу возникает вопрос: а сколько у него диагоналей? Учитывая, что из каждой из 12 вершин выходит девять диагоналей, получаем ответ: (12 · 9)/2 = 54 диагонали. Подумайте, почему произведение уменьшено в 2 раза.

Диагонали многоугольника, пересекаясь словно нитки искусной мастерицы, образуют симпатичную кружевную салфетку. Все внутренние узлы этой салфетки, кроме центрального, образованы пересечениями двух, трёх или четырёх отрезков (а в центре пересекаются шесть диагоналей). Например, убедитесь, что диагонали А₁А₄, А₂А₅ и А₃А₉ пересекаются в одной точке. Все диагонали двенадцатиугольника разбивают его только на треугольные и четырёхугольные части.

В скольких точках пересекаются диагонали двенадцатиугольника? Уточним, что вершины тоже являются точками пересечения диагоналей. Как решить эту, прямо скажем, скучную задачу? Но математику приходится иногда это делать. Чтобы облегчить себе жизнь, можно, например, подсчитать точки пересечения в одном из двенадцати секторов (рис. 5) с таким расчётом, чтобы точки не повторялись при поворотах, и добавить ещё одну центральную точку. Получим 12 · 26 + 1 = 313 точек.

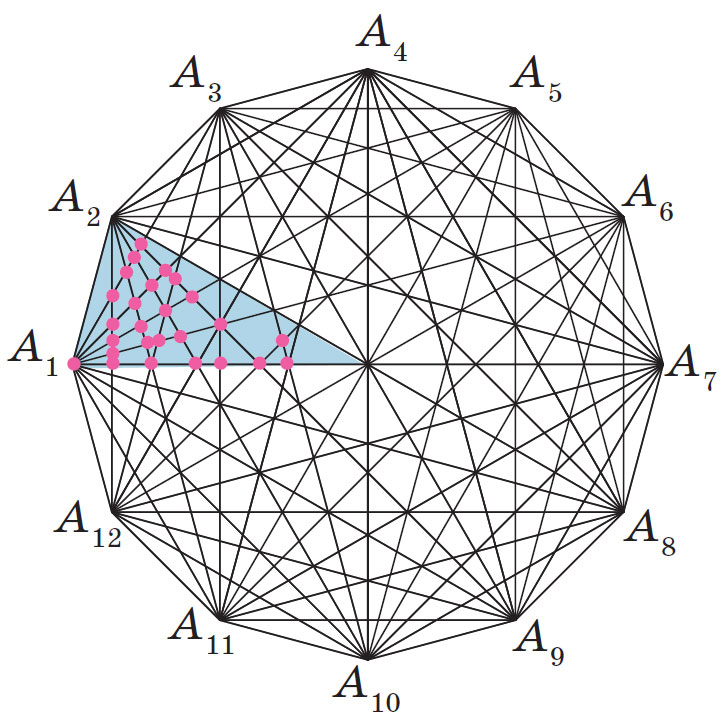
Рис. 5

Применяя такой же приём, подсчитаем, на сколько частей делят двенадцатиугольник его диагонали. Рассмотрим тот же сектор, в котором 20 синих и 17 белых частей, поэтому всего 12(20 + 17) = 444 части, из которых 276 — треугольники и 168 — четырёхугольники (рис. 6).

Рис. 6

Стороны двенадцати угольника и его диагонали образуют большое количество многоугольников, все вершины которых являются вершинами данного двенадцатиугольника. На рисунке 7 изображены два из них — пятиугольник и семиугольник. Сравните число таких пятиугольников с числом семиугольников.

Рис. 7

Считать не обязательно! Можно заметить, что каждому семиугольнику соответствует только один пятиугольник, вершинами которого являются те вершины двенадцатиугольника, которые не являются вершинами семиугольника. То есть между пятиугольниками и семиугольниками существует взаимно однозначное соответствие, поэтому их поровну.

Среди точек пересечения диагоналей можно выделить подмножества, принадлежащие одной окружности. Если раскрасить вот такой «павлиний хвост», как на рисунке 8, то «зелёные» точки лежат на «зелёных» окружностях, а «жёлтые» точки — на «жёлтых» окружностях. Почему? Всё становится понятным, если вспомнить, что угол с вершиной внутри окружности измеряется полусуммой двух дуг этой окружности, одна из которых заключена между его сторонами, а другая — между их продолжениями.

Рис. 8

Если двенадцатиугольную «салфетку» раскрасить как на рисунке 9, то можно заметить, что двенадцатиугольник состоит из 6 квадратов, 6 равносторонних треугольников и одного шестиугольника в центре. Но этот правильный шестиугольник состоит ещё из 6 равносторонних треугольников. Поэтому площадь правильного двенадцатиугольника со стороной a равна сумме площадей 6 квадратов со стороной a и 12 равносторонних треугольников со стороной a.

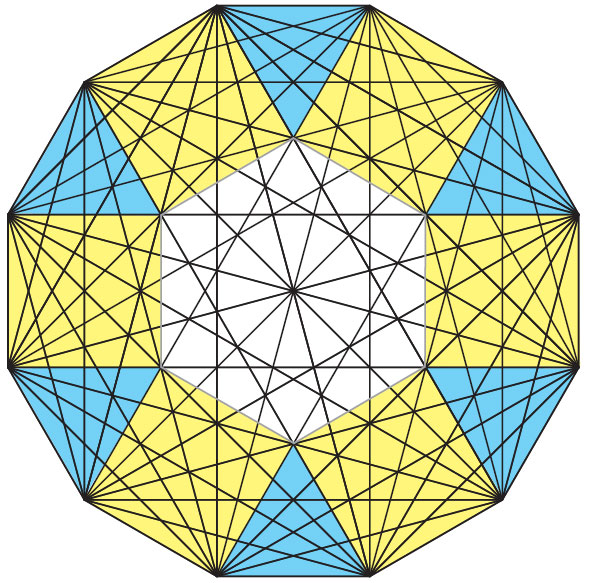
Рис. 9

И в заключение — два интересных непростых факта, замаскированных в «дебрях» диагоналей двенадцатиугольника. Оказывается, следующие тройки точек образуют правильные треугольники: середина стороны A₁A₂, середина диагонали A₃A₇, середина диагонали A₉A₁₂ (рис. 10), а также вершина A₃, точка пересечения диагоналей A₄A₈ и A₆A₁₀, точка пересечения диагоналей A₁A₁₁ и А₈А₁₂ (рис. 11).

Рис. 10

Рис. 11

¹ См. также статью «Знакомьтесь: двенадцатиугольник» по материалам кружка Д. Калинина в «Квантике» №7 за 2014 год.