Мозаика Робинсона
Хайдар Нурлигареев
«Квантик» №10, 2020

Эта статья из «Квантика» — переработанная версия одноименной картинки дня на «Элементах». Поскольку журнал «Квантик» в первую очередь предназначен для школьников, то основные изменения были направлены в сторону упрощения текста: больше внимания уделено описанию конструкции мозаики, несколько меньше — обсуждению ее свойств и объяснению идей доказательств, при этом тексты сильно пересекаются. Если вы не боитесь математических сложностей, то рекомендуем также прочитать картинку дня «Мозаика Робинсона».
Пусть имеется конечный набор многоугольников и есть возможность изготовить сколько угодно копий каждого из них. Цель — замостить всю плоскость, используя лишь такие копии (будем называть их плитками). Бывает, что замощение получается только периодическое. Например, если в наборе лишь один правильный шестиугольник, или же лишь одна фигурка крест-пентамино (рис. 1). А иногда можно замостить и периодически, и непериодически. Скажем, если в наборе только квадрат или только правильный треугольник (рис. 2).


Рис. 2
Кстати, а что такое «периодическое» замощение? Первое, что приходит в голову, — это замощение можно сдвинуть на какое-то расстояние в каком-то направлении, и оно идеально наложится само на себя. Но тогда и правое замощение на рисунке 2 периодическое. Мы же имеем в виду картинки, похожие на рисунок 1. Поэтому правильное определение такое: замощение периодическое, если можно сделать два каких-то сдвига в непараллельных направлениях так, что замощение совместится само с собой.
Удивительнее всего, что бывают наборы фигур, копиями которых можно замостить плоскость только непериодически. До середины XX века считалось, что их не существует, пока в 1966 году Роберт Бергер не сконструировал первый такой набор, состоящий аж из 20 426 различных плиток. Немного позже сам же Бергер уменьшил число различных многоугольников до 104, а в течение следующего десятилетия усилиями ряда учёных удалось понизить его до 2 — искомый пример доставляют знаменитые мозаики Пенроуза. Существует ли набор из единственного многоугольника, копиями которого можно замостить плоскость лишь непериодически, неизвестно до сих пор.
Мы расскажем о таком наборе из 6 многоугольников, который предложил Рафаэль Робинсон в 1971 году (рис. 3). Выступы и пазы на этих плитках организованы так, чтобы рисунок на прикладываемых друг к другу плитках был согласован: синие линии на одной плитке продолжаются на соседних плитках синими линиями, а красные с фиолетовым краем — красными с фиолетовым краем (причём фиолетовые края стыкуются). Кроме того, плитка A отличается от остальных плиток формой углов: у неё это квадратные выступы, тогда как углы остальных плиток обрезаны.

Рис. 3
Мы наметим доказательство, почему такими плитками можно замостить плоскость, но только непериодически. Часто, чтобы убедиться в справедливости очередного утверждения, надо будет перебрать несколько вариантов — будьте к этому готовы.

Рис. 4
Пусть мы замостили плоскость, используя лишь копии этих 6 плиток (будем обозначать их соответствующими буквами, как на рисунке 3). Хоть одна плитка A обязательно встретится в замощении (почему? — обратите внимание на выступы по углам); для определённости будем считать, что красные выступы этой плитки A торчат вправо и вверх. Ясно, что среди её соседей нет плитки A (рис. 4). Что стоит на месте вопросительных знаков? Если и там, и там не плитка A, то правый сосед у верхнего знака вопроса и верхний сосед у правого знака вопроса — две плитки A, и они перекрываются (убедитесь в этом). Значит, один из знаков вопроса — плитка A.
Будем считать, что A — клетка справа от исходной. Тогда клетка между ними — С или Е, а красные выступы второй клетки A торчат влево и вверх (рис. 5). В любом случае у плитки посередине на верхней стороне есть паз.
Заметим, что выступы плиток, стоящих над нашими двумя плитками A, не могут смотреть «друг на друга», то есть в сторону плитки между ними. Значит, между ними может находиться только плитка В (рис. 6). Но плитки A и В не могут стоять рядом. Следовательно, над плиткой В стоит не А. В двух ещё не заполненных углах квадрата 3 × 3 стоят плитки A, потому что к уголку из трёх плиток «не А» должна примыкать плитка A. Нетрудно понять, что красные выступы четырёх плиток A смотрят друг на друга. У нас есть возможность выбрать одну из четырёх ориентаций плитки В, но как только мы её зафиксируем, оставшиеся четыре позиции квадрата 3 × 3 заполняются однозначно (рис. 7).
Оказывается, сконструированные подобным образом квадраты 3 × 3 — так называемые макроплитки — ведут себя точно так же, как и плитки A. Именно, единственная возможность соединить их между собой — расположить их по углам квадрата 7 × 7; выходящие при этом из середин сторон макроплиток красные линии должны смотреть друг на друга. Снова по центру должна располагаться плитка В, а зафиксировав одну из четырёх её ориентаций, мы однозначно заполняем оставшиеся промежутки и получаем супермакроплитку (рис. 8).
Можно доказать, что этот процесс укрупнения продолжается и дальше. Так возникает иерархия квадратов размера 1 × 1, 3 × 3, 7 × 7, 15 × 15, 31 × 31, ... , (2n − 1) × (2n − 1), ... , каждый из которых наделён узором: какие-то две из выходящих по центру его сторон линии — красные, две другие — синие. Когда мы объединяем макроплитки в супермакроплитки, красные линии сливаются в квадрат, благодаря чему образуется иерархия красных квадратов размера 2 × 2, 4 × 4, 8 × 8, 16 × 16, 32 × 32, ..., 2n × 2n, ... соответственно. Эти красные квадраты объясняют удивительные свойства замощений плитками Робинсона.
Например, любое замощение плоскости плитками Робинсона — непериодическое. Иначе можно было бы переместить все плитки замощения на одинаковое расстояние так, что мы бы не увидели разницы. В частности, красные квадраты должны были бы перейти в такие же красные квадраты. Но так как в любом замощении плитками Робинсона найдутся сколь угодно большие красные квадраты, а квадраты одного размера не пересекаются между собой, это невозможно. Ведь на какое бы конечное расстояние мы ни сдвинулись, найдётся настолько большой квадрат, что за его пределы мы не выйдем. А значит, этот квадрат наложится сам на себя.

Рис. 9
А как тогда устроены замощения плитками Робинсона и почему они вообще существуют? Чтобы понять это, поглядим более внимательно на процесс укрупнения, благодаря которому удаётся перейти от отдельных плиток к замощению всей плоскости в целом. Рассмотрим какую-нибудь плитку A. Она входит в макроплитку размера 3 × 3 в одном из четырёх положений, которые мы обозначим цифрами 1, 2, 3 и 4 (рис. 9). Аналогично, макроплитка входит в супермакроплитку в одном из четырёх положений, и т. д. Таким образом, если нам дано некоторое замощение плоскости, то каждой плитке мы можем сопоставить бесконечную последовательность из цифр 1, 2, 3 и 4. Например, пусть дано замощение, изображённое на рисунке 10, и мы стартуем с зелёной плитки. Тогда первый элемент последовательности равен 3, поскольку зелёная плитка входит в оранжевую макроплитку в третьем положении. Затем, второй элемент — 1, так как оранжевая макроплитка входит в бежевую супермакроплитку в первом положении. Аналогично, третий элемент — 2, четвёртый — 4, и т. д. То есть зелёной плитке сопоставляется последовательность 3124...
Верно и обратное, то есть любой последовательности из цифр 1, 2, 3 и 4 мы можем сопоставить некоторое замощение. Правда, некоторым последовательностям будет соответствовать замощение не всей плоскости, а только её части. Например, если мы возьмём последовательность 222222..., то получим замощение четверти плоскости, а если 131313... — то полуплоскости. Подобные куски можно «склеить» между собой, так что возникнет замощение всей плоскости с исключительными линиями — прямыми или лучами (рис. 11).
Но замощения, в которых есть исключительные полосы, — редкость, их доля исчезающе мала. Ведь наличие исключительной полосы означает, что в последовательность, соответствующую какой-либо плитке такого замощения, с какого-то момента входит не больше двух чисел из четырёх. Такого почти не бывает: это как если бы мы подбрасывали «честную» монетку, и вдруг с какого-то момента всегда стала выпадать решка. Так что подавляющее большинство замощений плитками Робинсона выглядят примерно как на рисунке 10.
Ещё из интересных свойств: в замощениях плитками Робинсона любой «типичный» фрагмент встречается бесконечно много раз: чтобы убедиться в этом, достаточно найти красный квадрат, содержащий этот фрагмент. Раз квадратов одного и того же размера бесконечно много, то и фрагментов заданного вида внутри них — тоже.
В замощениях, как на рисунке 11, есть фрагменты (бежевые), не содержащиеся ни в одном из красных квадратов, — они примыкают к исключительным линиям или пересекают их. Несмотря на это, они всё равно встречаются в замощении бесконечно много раз. Правда, часть из них можно найти только при движении вдоль исключительной полосы.
Художник Алексей Вайнер
Мозаики и замощения
-
 28.01.2026Памяти Сергея Валерьевича Маркелова (17.02.1976–11.12.2024)Александр Буфетов • Библиотека • «Троицкий вариант» №25(444), 2025
28.01.2026Памяти Сергея Валерьевича Маркелова (17.02.1976–11.12.2024)Александр Буфетов • Библиотека • «Троицкий вариант» №25(444), 2025 -
 28.04.2023Замощение Соколара — ТейлорМихаил Грунтов, Хайдар Нурлигареев • Картинки дня
28.04.2023Замощение Соколара — ТейлорМихаил Грунтов, Хайдар Нурлигареев • Картинки дня
-
 28.04.2023Решена «задача Эйнштейна» о замощении плоскостиХайдар Нурлигареев • Новости науки
28.04.2023Решена «задача Эйнштейна» о замощении плоскостиХайдар Нурлигареев • Новости науки
-
 29.08.2021Теорема Наполеона, замощения плоскости и параллельникиГригорий Мерзон • Библиотека • «Квантик» №12, 2020
29.08.2021Теорема Наполеона, замощения плоскости и параллельникиГригорий Мерзон • Библиотека • «Квантик» №12, 2020
-
 21.07.2021Замощения параллелоэдрамиАлексей Гарбер • Библиотека • «Квант» №1, 2019
21.07.2021Замощения параллелоэдрамиАлексей Гарбер • Библиотека • «Квант» №1, 2019
-
 03.06.2021Мозаика РобинсонаХайдар Нурлигареев • Библиотека • «Квантик» №10, 2020
03.06.2021Мозаика РобинсонаХайдар Нурлигареев • Библиотека • «Квантик» №10, 2020
-
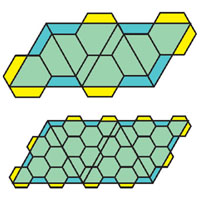 30.05.2021Оклейка тетраэдра шестиугольникамиНиколай Авилов • Библиотека • «Квант» №10, 2018
30.05.2021Оклейка тетраэдра шестиугольникамиНиколай Авилов • Библиотека • «Квант» №10, 2018
-
 06.12.2020Как разрезать верблюда?Григорий Мерзон • Библиотека • «Квантик» №5, 2020
06.12.2020Как разрезать верблюда?Григорий Мерзон • Библиотека • «Квантик» №5, 2020
-
 03.06.2020Плитки и числа ХеешаХайдар Нурлигареев • Библиотека • «Квантик» №10, 2019
03.06.2020Плитки и числа ХеешаХайдар Нурлигареев • Библиотека • «Квантик» №10, 2019
-
 09.08.2019Ковер СерпинскогоХайдар Нурлигареев • Картинки дня
09.08.2019Ковер СерпинскогоХайдар Нурлигареев • Картинки дня



















Рис. 1