Игры Конвея, рисунки Эйлера и прочие проблемы

Григорий Мерзон
«Квантик» №11, 2020

1. Игра Конвея. В «Квантике» № 10 за 2020 год предлагалась следующая «игра в ростки» Дж. Конвея.

Рис. 1

На плоскости нарисовано N крестиков. Двое ходят по очереди. За ход нужно соединить два свободных конца (в начале у каждого крестика по 4 свободных конца) линией, не пересекающей уже проведённые, и поставить на ней засечку (при этом образуется два новых свободных конца; на рисунке 1 пример положения после двух ходов для N = 2). Тот, кто не может сделать ход, проигрывает. Кто — начинающий или второй игрок — может выиграть, как бы ни играл соперник?

Задумаемся над тем, почему партия вообще заканчивается.

Игроки делят плоскость на грани (регионы). Партия закончится, когда каждый из 4N свободных концов — их количество не меняется в ходе игры! — окажется в отдельной грани.

Подумаем теперь, как появляются новые грани. Каждая новая линия либо соединяет две компоненты связности (части) рисунка — и тогда новых граней не появляется («ход первого типа», рис. 2, а), либо соединяет два конца в одной компоненте связности — и тогда одна грань разделяется на две («ход второго типа», рис. 2, б).

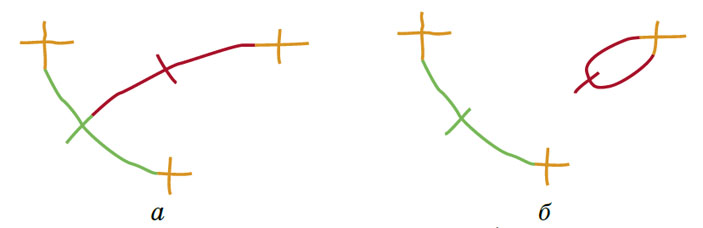
Рис. 2. Два типа ходов: а) минус одна компонента связности; б) плюс одна грань

Заметим, что в каждой грани обязательно остаётся хотя бы один свободный конец, поэтому граней не может стать больше, чем концов.

Итак, в начале партии у рисунка N компонент связности, в конце — одна, поэтому всего будет N − 1 ходов первого типа. В начале партии грань одна, а в конце — столько же, сколько свободных концов, 4N, поэтому всего будет 4N − 1 ходов второго типа.

То есть всего будет сделано N − 1 + 4N − 1 = 5N − 2 ходов. Получается, что «игра в ростки» — это игра-шутка: что бы ни делали игроки, если число 5N − 2 нечётно, то делает последний ход и выигрывает первый, если чётно — второй.

2. Формула Эйлера. Каждый знает, что у многоугольника столько же вершин, сколько сторон. А какой аналог этого утверждения для многогранников? У многогранника можно сосчитать количество вершин (V), рёбер (E), граней (F). Но, зная только одну из этих величин, нельзя определить другие — см. таблицу.

И всё же между этими тремя величинами, как мы увидим, есть связь!

Перейдём, во-первых, к изображениям многогранников на плоскости, причём таким, на которых рёбра не пересекаются. Например, можно подойти к одной из граней и сфотографировать многогранник сквозь неё, используя сверхширокоугольный объектив, — получатся картинки типа изображённых на рисунке 3.

Рис. 3

Действуем примерно как в предыдущем разделе: на чистом листе бумаги отметим сначала V вершин, а дальше будем проводить рёбра по одному.

Каждое новое ребро — это линия, которая либо соединяет две компоненты связности (рис. 4, а), не меняя числа регионов, либо (если ребро соединяет две вершины в одной компоненте связности) делит один из имеющихся регионов на два (рис. 4, б).

Рис. 4. Два типа ходов: а) минус одна компонента связности; б) плюс одна грань

В начале компонент связности V, в конце — одна; в начале вся плоскость представляет собой один регион, в конце будет F регионов (граней). Поэтому из E проведённых рёбер было V − 1 первого типа и F − 1 второго типа. Значит, E = (V − 1) + (F − 1). Мы получили следующую формулу Эйлера.

Если у многогранника V вершин, E рёбер, F граней, то V − E + F = 2.

На плоскости можно нарисовать правильный N-угольник для любого N. А вот правильных многогранников существует всего пять! И это можно доказать при помощи формулы Эйлера.

Но сначала нужно дать определение правильного многогранника (как ни странно, это не так просто). Мы примем такое: выпуклый многогранник называется правильным, если все его грани — правильные многоугольники, а в каждой вершине сходится одно и то же количество граней.

Задача 2. а) Выведите из формулы Эйлера, что если у многогранника все грани — n-угольники, а в каждой вершине сходится по k граней, то

б) Докажите, что все правильные многогранники изображены на рисунке 5 (то есть n = 3, k = 3, или n = 3, k = 4, или n =4, k = 3, или n = 3, k = 5, или n = 5, k = 3).

Рис. 5

3. Доказательства и опровержения. Существует ли многогранник, все грани которого — шестиугольники?

Пусть у такого многогранника F граней. В каждой грани 6 рёбер, а каждое ребро входит ровно в 2 грани — значит, 2E = 6F. В каждой грани 6 вершин, в каждой вершине сходится не меньше 3 граней — значит, 3V ≤ 6F. Итак, E = 3F, V ≤ 2F. Но тогда V − E + F ≤ 2F − 3F + F = 0. А по формуле Эйлера эта сумма должна быть равна 2. Значит, таких многогранников не бывает.

По аналогичным причинам не бывает многогранника, все грани которого семиугольники (и т. д.). Но примеры таких многогранников приведены в «Квантике» № 4 за 2020 год! (Заметка «Многогранник из семиугольников?».)

Мораль тут такая: хотя приведённое рассуждение «по сути правильное», полным доказательством его считать не стоит, а опираться на «примерно понятные» рассуждения — дело опасное...

Закончим цитатой из одноимённой с этим разделом книги И. Лакатоша, которая вся состоит из обсуждения доказательств формулы Эйлера и возникающих при этом вопросов:

Сигма. Но ведь ничего не установлено. Мы не можем остановиться теперь.

Учитель. Сочувствую вам. Эта последняя стадия даст важные источники пищи для нашей дискуссии. Но научное исследование «начинается и кончается проблемами». (Покидает классную комнату.)

Бета. Но вначале у меня не было проблем! А теперь у меня нет ничего, кроме проблем!

Художник Мария Усеинова