Точка Торричелли и сети Штейнера (продолжение)

Владимир Протасов
«Квантик» №11, 2021

Начало — в «Квантике» №10, 2022.

Иногда полезно по-разному доказать один и тот же факт. Это позволяет посмотреть на него с разных сторон. Чтобы ощутить красоту скульптуры — надо обойти её вокруг! Теорема о точке Торричелли (из которой каждая сторона треугольника видна под углом 120°) — не исключение. Вот, например, как доказать её с помощью площадей.

Площади и теорема о трёх расстояниях

Начнём с такого замечательного факта:

Теорема 5 (о трёх расстояниях). Сумма расстояний от любой точки внутри равностороннего треугольника до его сторон равна высоте треугольника.

Рис. 7

Значит, для любой точки M внутри треугольника эта сумма одна и та же. Чтобы доказать это, обозначим сторону и высоту исходного треугольника через a и h и соединим M c вершинами. Исходный треугольник разобьётся на три меньших. А теперь вспомним, что площадь треугольника — это половина произведения его стороны на высоту, проведённую к этой стороне. Высоты меньших треугольников — это как раз расстояния до сторон исходного треугольника, и опущены они на стороны одной и той же длины a. Поэтому сумма этих расстояний, умноженная на a, равна удвоенной площади исходного треугольника, то есть равна произведению ah. Сокращая на a, получаем требуемое.

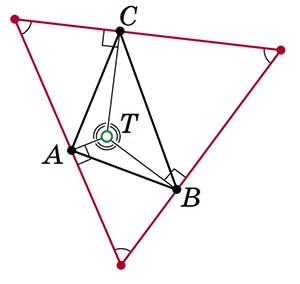
Рис. 8

Ну и какая тут связь с точкой, сумма расстояний от которой до сторон наименьшая (задача  3 из прошлого номера)? Возьмём произвольный треугольник ABC и  его точку Торричелли T (предполагаем, что она есть). Проведём через вершину A прямую, перпендикулярную отрезку TA. Так же сделаем с двумя другими вершинами (рис. 8). Три получившиеся прямые образуют треугольник. Он равносторонний: все его углы равны 60° (почему?). Сумма расстояний от точки T до сторон равностороннего треугольника (она же — сумма расстояний от T до вершин треугольника ABC) равна его высоте. И сумма расстояний от любой другой точки M до его сторон тоже равна высоте. Но теперь эта сумма будет меньше, чем сумма расстояний от M до вершин ABC, ведь расстояние до каждой вершины больше расстояния до стороны (наклонная больше перпендикуляра). Получается, что сумма расстояний от M до вершин треугольника ABC больше, чем сумма расстояний от точки T.

Немного физики

Как мы упоминали, сам Торричелли, по-видимому, вывел свою теорему из физических соображений. Мы не знаем, каких именно, но тоже попробуем получить физическое доказательство. Хотя нам понадобятся понятие потенциальной энергии и закон сложения сил, рассуждение будет интуитивно понятным.

Рис. 9

Представим, что треугольник ABC нарисован на столе. Просверлим три дырки в вершинах A, B и C и  пропустим в них по верёвке. Все три верёвки свяжем узлом над столом, а под столом к каждой верёвке привесим груз в 1 кг. Отпустим верёвки и грузы. Вся система после колебаний придёт в равновесие (рис.  9). Мы утверждаем, что в положении равновесия узел попадёт ровно в точку Торричелли треугольника ABC. Это следует из такого физического принципа: механическая система достигает равновесия, когда её потенциальная энергия минимальна. Иными словами, любая система стремится уменьшить свою потенциальную энергию. И  останавливается, когда уменьшать уже некуда. Мы наблюдаем это каждый день повсюду: если отпустить растянутую пружину, она снова сожмётся; брошенный вверх камень упадёт вниз и т. п.

У каждого груза потенциальная энергия пропорциональна его высоте над полом. Поэтому грузы стремятся уменьшить суммарную высоту, то есть вытянуть вниз как можно больше верёвки. Тем самым равновесие придёт, когда станет минимальной суммарная длина MA+MB+MC верёвок на столе.

На точку M действуют три силы, равные весам грузов. Грузы равны, поэтому и силы равны. А в положении равновесия точка M не движется, поэтому сумма сил равна нулю. Сумма равных по величине сил равна нулю, когда все углы между ними равны по 120°. В  самом деле, сложив силы, получаем, что они должны образовать треугольник, и он будет равносторонним. Поэтому силы образуют между собою равные углы. Следовательно, M — точка Торричелли.

Сети Штейнера

Ну, а теперь примемся за построение кратчайших систем дорог для любого числа городов — сетей Штейнера. Мы считаем известным, что кратчайшая система существует (это не так очевидно, как может показаться). Города нам даны, мы не можем менять их расположение. Но проводить дороги и ставить перекрёстки можем как хотим. Город и перекрёсток будем называть одним словом — вершина. Каждая дорога соединяет какие-нибудь две вершины. Ясно, что у кратчайшей системы все дороги прямые. Любой путь по дорогам от одной вершины до другой будем просто называть путём. Значит, все дороги — отрезки, а пути  — ломаные. Найдём несколько обязательных свойств, которыми обладает кратчайшая система.

Свойство 1. Каждые две вершины связывает единственный путь, а замкнутых путей нет.

Это просто: если есть замкнутый путь, то его можно «разорвать», убрав любую дорогу. Общая длина дорог уменьшится, но из любого города по-прежнему можно проехать в любой другой. А если бы существовало два пути из одной вершины в другую, то они образовали бы замкнутый путь (для этого нужно один из путей проехать в обратном направлении).

Для следующего свойства нам понадобится вспомогательный факт: Любые две дороги, исходящие из одной вершины, образуют угол, не меньший 120°.

Предположим обратное: дороги MA и MB образуют угол, меньший 120°. Если два других угла треугольника AMB тоже меньше 120°, то у него есть точка Торричелли T. Поставим в ней новый перекрёсток, уберём дороги MA и MB, а вместо них сделаем три дороги, TA, TB и TМ. Сумма длин всех дорог от этого уменьшится, потому что сумма длин трёх новых дорог меньше, чем двух старых (сумма расстояний до вершин треугольника АМВ от точки Торричелли T меньше, чем от точки M). Значит, мы уменьшили общую длину дорог.

Если же один из двух других углов треугольника AMB, скажем, угол A, не меньше 120°, то уберём дорогу MB, а вместо неё сделаем новую дорогу MA. Заметим, что MB длиннее MA, поскольку лежит на против наибольшего угла треугольника. Значит, мы убрали длинную дорогу, заменив её короткой, то есть вновь уменьшили общую длину дорог.

Свойство 2. Из каждого города выходит либо одна дорога, либо две, угол между которыми не меньше 120°, либо три под углами 120°.

Четырёх быть не может, иначе среди них найдутся две дороги, образующие угол, меньший 120°. Если выходят три дороги, то все углы между ними равны по 120°, иначе опять-таки нашлись бы две дороги с углом меньше 120°.

Свойство 3. Из каждого перекрёстка исходят ровно три дороги под углами 120° друг к другу.

Из перекрёстка не может выходить одна дорога, иначе эту дорогу вместе с перекрёстком можно убрать. Также не может выходить две дороги. Иначе можно убрать эти дороги вместе с перекрёстком, а их концы соединить напрямую. Так что из каждого перекрёстка исходит ровно три дороги, и они образуют углы в 120°.

Подведём итоги. Сеть Штейнера обязана обладать свойствами 1, 2, 3: у неё нет замкнутых путей, в каждом перекрёстке сходятся три дороги под углами 120°, а в каждом городе либо сходятся три дороги под углами 120°, либо две дороги под углом не менее 120°, либо только одна дорога.

Дорожную сеть, обладающую свойствами 1, 2, 3, мы будем называть допустимой. Сеть Штейнера всегда допустима. А наоборот? Любая ли допустимая дорожная сеть является сетью Штейнера? Вообще говоря, нет. На рисунке 10 — три допустимые сети для одного и того же набора городов, и все они имеют разную длину. И тем не менее, свойств 1, 2, 3 хватит для построения сети Штейнера.

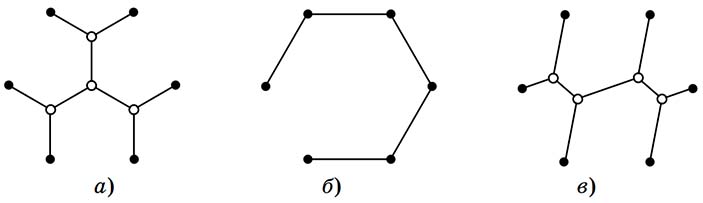
Рис. 10

В следующем номере мы научимся строить сети Штейнера

Окончание следует

Художник Алексей Вайнер