Калейдоскопы
Эрнест Винберг
«Квант» №6, 2020
В мае 2020 года ушел из жизни выдающийся математик, профессор Московского государственного университета имени М. В. Ломоносова и Независимого Московского университета Э. Б. Винберг. Эрнест Борисович — автор большого числа книг и учебников для студентов и школьников, многие годы он был главным редактором сборника «Математическое просвещение».
В предисловии к своему замечательному учебнику «Курс алгебры» Э. Б. Винберг пишет: «В соответствии со своим взглядом на математику я стремился заменить выкладки и сложные рассуждения идеями. Кому-то это может показаться трудным, но усилия, потраченные на освоение идей, окупятся возможностью самостоятельно решать задачи, не рассматриваемые в учебнике». Эрнест Борисович придерживался этого принципа на протяжении всех лет занятий математикой и преподавания. Это одна из причин, по которой работы Винберга написаны столь ясно, а лекции и выступления на семинарах так хорошо структурированы и увлекательны.
Предлагаем вашему вниманию статью Э. Б. Винберга, опубликованную в «Соросовском образовательном журнале» (1997, №2)
Калейдоскоп (что в переводе с греческого означает ‘смотрю красивый вид’) — это детская игрушка, в которой разноцветные кусочки стекла, многократно отражаясь в трех зеркалах, создают красивый узор. Зеркала эти расположены как боковые грани правильной треугольной призмы, образуя между собой углы, равные π/3. Если бы эти углы были другими, то отражения накладывались бы друг на друга и не создавали симметричного узора. Однако имеются исключительные случаи, когда этого не происходит. Все они могут быть легко найдены, что и будет сделано в разделе 2.
Описанный выше обычный калейдоскоп по существу двумерен, так как мы видим в нем плоский узор. Можно представить себе трехмерный калейдоскоп как многогранную камеру с зеркальными стенками. Наблюдатель, помещенный в нее, увидит многократные отражения всех находящихся в ней предметов. Как правило, эти отражения будут перекрываться, но есть несколько случаев (мы их опишем в разделе 4), когда отражения не перекрываются и создают симметричный трехмерный узор.
Если отбросить в сторону возможность практической реализации, то можно говорить и о многомерных калейдоскопах, а также о неевклидовых калейдоскопах, а именно о калейдоскопах на сфере и в пространстве Лобачевского. Калейдоскопы в евклидовом пространстве и на сфере любой размерности были исчерпывающим образом описаны английским математиком Г. С. М. Кокстером в 1934 году. На обложке его переведенной на русский язык популярной книги [1] изображен один из калейдоскопов на обычной (двумерной) сфере (см. рис. 4). Сферические калейдоскопы тесно связаны с правильными многогранниками (см. раздел 3).
Калейдоскопы на плоскости Лобачевского использовались еще в конце прошлого века А. Пуанкаре и Ф. Клейном в их исследованиях по теории автоморфных функций комплексного переменного. В 1958–1960 годах голландский художник М. К. Эшер создал несколько оригинальных картин-узоров на базе этих калейдоскопов (таких, как на рисунке 5).
Калейдоскопы в пространстве Лобачевского стали объектом интенсивных исследований начиная с 1965 года в связи с некоторыми проблемами теории групп. Их полное описание в любой размерности еще далеко от завершения. Имеется удивительный результат (принадлежащий автору статьи) о том, что при n ≥ 30 в n-мерном пространстве Лобачевского вообще не существует калейдоскопов. Примеры таких калейдоскопов известны лишь при n ≤ 8.
Помимо уже упоминавшихся приложений калейдоскопов в геометрии (правильные многогранники), теории функций комплексного переменного и теории групп имеются не менее важные их приложения в теории чисел, теории алгебр Ли, алгебраической геометрии и других разделах математики. Следует, впрочем, сказать, что в серьезной математической литературе термин «калейдоскоп» не употребляется. Вместо этого говорят «дискретная группа, порожденная отражениями».
В статье мы не имеем возможности говорить о приложениях калейдоскопов (за исключением связи сферических калейдоскопов с правильными многогранниками). Однако изучение калейдоскопов самих по себе составляет яркую страницу геометрии. Более полные сведения о калейдоскопах можно найти в обзорной статье [2].
1. Основное свойство калейдоскопов
Рассмотрим простейшую ситуацию — два зеркала, расположенные под некоторым углом α одно к другому. Если угол α не является целой частью π, то, как показано на рисунке 1, а, изображения предмета, помещенного между зеркалами, будут перекрываться, так что в одной точке мы будем видеть изображения двух разных точек. (На самом деле мы сможем увидеть в одной точке изображения двух разных точек не одновременно, а только перемещая точку зрения, но это не имеет отношения к нашему теоретическому обсуждению.) Если же угол α является целой частью π, как, например, на рисунке 1, б, то этого не происходит.

Так как изображения каждой точки не выходят за пределы плоскости, перпендикулярной общей оси наших зеркал (именно такая плоскость и изображена на рисунке 1), то обнаруженное нами явление по существу двумерно. Можно говорить о зеркальном отражении плоских фигур относительно прямых, и рисунок 1 демонстрирует, что изображения, полученные многократными отражениями относительно сторон угла, не перекрываются тогда и только тогда, когда величина α этого угла является целой частью π. Более точно, если α = π/k, где k ≥ 2 — натуральное число, то вся плоскость оказывается разбитой на 2k равных углов с общей вершиной, в каждом из которых получается одно изображение внутренности исходного угла. В половине из этих углов изображения являются зеркально обращенными, в другой половине, включающей сам исходный угол, — необращенными.
Представим себе теперь выпуклый многоугольник, образованный зеркалами. В каком случае изображения, получаемые многократными отражениями внутренности многоугольника относительно его сторон, не будут перекрываться? Из предыдущего следует, что для этого необходимо, чтобы все углы многоугольника были целыми частями π. Можно показать, что это условие является и достаточным. Если оно выполнено, то вся плоскость оказывается разбитой на многоугольники, равные исходному, таким образом, что любые два многоугольника, имеющие общую сторону, симметричны относительно этой стороны. В каждом из многоугольников этого разбиения получается одно изображение внутренности исходного многоугольника. На рисунке 2 показано разбиение плоскости, получаемое из равностороннего треугольника. Именно это разбиение мы видим, глядя в обычный калейдоскоп.

Рис. 2. Обычный калейдоскоп
Точно так же изображения, получаемые многократными отражениями внутренности выпуклого многогранника относительно его граней, не перекрываются тогда и только тогда, когда все двугранные углы многогранника являются целыми частями π. Эта теорема справедлива и для неевклидовых многоугольников и многогранников.
Многоугольник (многогранник), все (двугранные) углы которого являются целыми частями π, называется многоугольником (многогранником) Кокстера. Таким образом, описание теоретически возможных калейдоскопов равносильно описанию многоугольников и многогранников Кокстера.
2. Двумерные калейдоскопы
Нетрудно найти все многоугольники Кокстера на евклидовой плоскости. Как известно, сумма углов евклидова n-угольника равна π(n − 2), так что среднее арифметическое его углов равно π(1 − 2/n), что при n = 4 составляет π/2. Но все углы многоугольника Кокстера, как явствует из определения, не больше π/2. Поэтому единственным четырехугольником Кокстера является прямоугольник, а многоугольников Кокстера с большим числом сторон вообще не существует.
Далее, так как сумма углов треугольника равна π, то для треугольника Кокстера с углами π/k, π/l, π/m мы получаем диофантово уравнение
С точностью до перестановки чисел k, l, m оно имеет три решения:
(3, 3, 3), (2, 4, 4), (2, 3, 6).
Таким образом, имеется ровно три треугольника Кокстера: равносторонний, равнобедренный прямоугольный и прямоугольный с острыми углами π/3 и π/6. Соответствующие разбиения плоскости изображены на рисунке 3. Вместе с прямоугольником это дает четыре типа двумерных евклидовых калейдоскопов.

Рис. 3. Двумерные евклидовы калейдоскопы
Аналогичным образом можно найти все двумерные сферические калейдоскопы. Сумма углов сферического n-угольника больше π(n − 2) (простое доказательство этого см., например, в [3]). Поэтому в отношении сферических многоугольников Кокстера наши выводы о числе сторон только усугубляются, а именно, не существует сферических многоугольников Кокстера, отличных от треугольника. Для сферического треугольника Кокстера уравнение (1) заменяется на неравенство
имеющее следующие решения:
(2, 2, m), (2, 3, 3), (2, 3, 4), (2, 3, 5).

Рис. 4. Сферический калейдоскоп
Первому из этих решений отвечает разбиение сферы на 4m «бипрямоугольных» треугольников, осуществляемое экватором и 2m равноотстоящими друг от друга меридианами. Решению (2, 3, 5) отвечает разбиение, изображенное на рисунке 4. В разделе 3 мы еще вернемся к сферическим калейдоскопам в связи с правильными многогранниками.
Что касается калейдоскопов на плоскости Лобачевского, то их гораздо больше. Все, что не может быть реализовано на евклидовой плоскости или сфере, реализуется на плоскости Лобачевского. А именно: сумма углов n-угольника на плоскости Лобачевского меньше π(n − 2), и для любых натуральных чисел k1, k2, ..., kn ≥ 2, удовлетворяющих неравенству
на плоскости Лобачевского имеется многоугольник Кокстера с углами π/k1, π/k2, ..., π/kn.
Предыдущее неравенство автоматически выполняется при n > 4, а также при n = 4, если только (k1, k2, k3, k4) ≠ (2, 2, 2, 2). При n = 3 мы получаем следующее неравенство для треугольника Кокстера с углами π/k, π/l, π/m:
Его решениями являются все тройки (k, l, m), кроме перечисленных выше решений уравнения (1) и неравенства (2).
Например, на плоскости Лобачевского имеется треугольный калейдоскоп с углами π/2, π/4, π/6. Соответствующее разбиение изображено на рисунке 5, а. При этом использована модель Пуанкаре, в которой плоскость Лобачевского изображается в виде открытого круга, ее прямые — в виде диаметров круга, а углы совпадают с евклидовыми. При приближении к границе круга евклидовы размеры треугольников разбиения стремятся к нулю, но их размеры в смысле геометрии Лобачевского, естественно, остаются постоянными. Рисунок 5, б представляет картину-узор Эшера, основанный на этом разбиении.

Рис. 5. Калейдоскоп на плоскости Лобачевского
3. Сферические калейдоскопы и правильные многогранники

Рис. 6. Фундаментальный конус куба
С каждым правильным многогранником можно связать сферический калейдоскоп. Пусть М — правильный многогранник с центром в точке О. Пусть А — центр какой либо его грани, В — середина какой-либо стороны этой грани и С — какая-либо из двух вершин, принадлежащих этой стороне. Трехгранный конус K с вершиной в точке О, ребра которого проходят через точки А, В, С соответственно, назовем фундаментальным конусом многогранника М (на рисунке 6 в качестве М взят куб).
За счет различного выбора грани, ее стороны и вершины, принадлежащей этой стороне, можно построить много разных фундаментальных конусов данного многогранника. Они не перекрываются и в совокупности покрывают все пространство. Их число N может быть подсчитано по любой из следующих формул:
где приняты следующие обозначения: Г — число граней многогранника М, Р — число его ребер, В — число его вершин, р — число сторон (каждой) грани, q — число ребер, выходящих из (каждой) вершины. Так, в случае куба
Г = 6, Р = 12, В = 8, р = 4, q = 3, N = 48.
Плоскость любой грани фундаментального конуса является плоскостью симметрии многогранника М, и любые два фундаментальных конуса, имеющие общую грань, симметричны относительно плоскости этой грани. Например, в случае куба плоскость ОАС есть плоскость симметрии, проходящая через два противоположных ребра; конус K′, симметричный конусу K относительно этой плоскости, есть фундаментальный конус, ребра которого проходят через точки А, С, B′ (см. рис. 6).
Ребро OA конуса K является общим ребром 2р фундаментальных конусов, имеющих при этом ребре один и тот же двугранный угол. Следовательно, двугранный угол конуса K при ребре OA равен π/p. Аналогично устанавливается, что двугранный угол при ребре ОВ равен π/2, а при ребре ОС равен π/q. Отсюда мы заключаем, что пересечение любого фундаментального конуса со сферой, концентрической многограннику М, есть прямоугольный сферический треугольник с острыми углами π/p и π/q. Любые два из этих треугольников, имеющие общую сторону, симметричны относительно нее. Тем самым мы получили сферический калейдоскоп.
При переходе от правильного многогранника к сферическому калейдоскопу теряется информация о том, какое из ребер OA и ОС фундаментального конуса проходило через центр грани, а какое — через вершину многогранника М. Если мы рассмотрим правильный многогранник M′, вершинами которого служат центры граней многогранника М, то ему будет соответствовать тот же сферический калейдоскоп. Такие правильные многогранники М и M′ называют двойственными друг другу. Так, например, куб двойствен октаэдру. Тетраэдр двойствен сам себе (точнее, правильному многограннику, который также является тетраэдром). При переходе от М к M′ числа p и q, а также Г и В меняются ролями.
Каждому из сферических калейдоскопов, определяемых решениями
(2, 3, 3), (2, 3, 4), (2, 3, 5)
неравенства (2), отвечает пара двойственных правильных многогранников. Эти пары суть {тетраэдр, тетраэдр}, {куб, октаэдр}, {додекаэдр, икосаэдр} соответственно. Решению (2, 2, m) не отвечает никакой правильный многогранник, так как по смыслу должно быть р, q ≥ 3.
Известно, что площадь сферического треугольника1 равна его угловому избытку, т.е. сумме его углов минус π. В частности, площадь прямоугольного сферического треугольника с острыми углами π/p и π/q равна (1/p + 1/q − 1/2)π. Так как площадь всей сферы равна 4π, то отсюда получается еще одна формула для числа N (cp. (4)):
Аналогичная связь существует между n-мерными правильными многогранниками и калейдоскопами на (n − 1)-мерной сфере. Интересно, что, в то время как в трехмерном пространстве существует пять правильных многогранников, в четырехмерном пространстве их шесть, а в n-мерном при n > 4 всего три (аналоги тетраэдра, куба и октаэдра).
4. Трехмерные калейдоскопы
Нахождение многогранников Кокстера затрудняется тем, что соотношения между двугранными углами многогранника не столь просты, как соотношение между углами многоугольника. При пересечении выпуклого многогранника М с маленькой сферой с центром в какой-либо его вершине С образуется выпуклый сферический многоугольник, углы которого равны двугранным углам многогранника М при соответствующих ребрах. Поэтому если, скажем, из вершины С выходит q ребер, то сумма двугранных углов при этих ребрах больше π(q − 2). Отсюда следует, что если все двугранные углы многогранника М не превосходят π/2 (например, если он является многогранником Кокстера), то из каждой его вершины выходят только три ребра. Многогранники, обладающие этим последним свойством, называются простыми. Так, тетраэдр и куб являются простыми многогранниками, а октаэдр — нет.
Этими простыми неравенствами, однако, не исчерпываются соотношения между двугранными углами выпуклого многогранника. Рассмотрим простейший случай, когда М — треугольная пирамида. Занумеруем как-либо ее грани и обозначим через αij = αji угол между i-й и j-й гранями. Средствами линейной алгебры легко доказывается, что двугранные углы евклидовой треугольной пирамиды связаны соотношением

Определитель, стоящий в левой части, есть определитель Грама единичных нормальных векторов к граням пирамиды. Его равенство нулю вытекает из линейной зависимости этих векторов2.
Заметим, что точно так же доказывается, что углы α, β, γ евклидова треугольника связаны соотношением

однако это соотношение при условии, что сумма любых двух из углов α, β, γ меньше π, оказывается равносильным тому, что α + β + γ = π. (Попробуйте это доказать!) Что касается соотношения (6), то оно, к сожалению, не приводится к такому простому виду.
Соотношение (6) вместе с выведенными перед этим неравенствами является необходимым и достаточным условием для того, чтобы в евклидовом пространстве существовала треугольная пирамида с двугранными углами αij. Пользуясь этим, можно найти все евклидовы треугольные пирамиды, двугранные углы которых являются целыми частями π. Их оказывается три. Они изображены на рисунке 7, где принято следующее соглашение: двугранные углы при непомеченных ребрах равны π/2, а при ребрах, перечеркнутых одной или двумя чертами, π/3 или π/4 соответственно. Нетрудно заметить, что первая из пирамид, изображенных на рисунке 7, плоскостью симметрии разрезается на две пирамиды, подобные второй, и так же третья пирамида получается из второй.
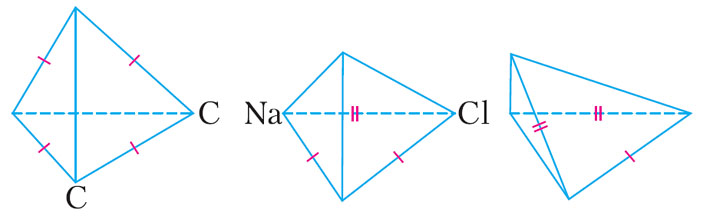
Рис. 7. Евклидовы треугольные пирамиды Кокстера
Кроме этих трех калейдоскопов в трехмерном евклидовом пространстве имеется еще только четыре калейдоскопа, которые в определенном смысле сводятся к двумерным. Это прямые призмы, в основании которых лежит двумерный калейдоскоп.
Трехмерные евклидовы калейдоскопы имеют непосредственное отношение к кристаллографии. Некоторые кристаллические решетки могут быть получены, если поместить определенным образом в такой калейдоскоп несколько атомов и рассмотреть все их изображения, получаемые многократными отражениями относительно стенок калейдоскопа. Так, кристаллическая решетка алмаза получается с помощью первого из калейдоскопов, изображенных на рисунке 7, если поместить в двух его вершинах, указанных на рисунке, атомы углерода С, а кристаллическая решетка поваренной соли получается с помощью второго калейдоскопа, если поместить в указанных на рисунке вершинах атомы натрия Na и хлора Cl.
Нетрудно также найти все калейдоскопы на трехмерной сфере. Все они представляют собой (сферические) треугольные пирамиды. Знак равенства в (6) заменяется в этом случае знаком «больше», подобно тому как при переходе от евклидовой плоскости к сфере сумма углов треугольника становится больше π.
5. Теорема Андреева
В пространстве Лобачевского знак равенства в (6) заменяется на знак «меньше». Нетрудно найти все многогранники Кокстера в пространстве Лобачевского, являющиеся треугольными пирамидами. Однако в этом случае они составляют лишь ничтожную часть всех многогранников Кокстера. Подобно тому как на плоскости Лобачевского существуют многоугольники Кокстера со сколь угодно большим (на самом деле любым) числом сторон, в пространстве Лобачевского существуют многогранники Кокстера со сколь угодно большим числом граней. Но в отличие от многоугольников они могут иметь весьма сложное комбинаторное строение. Поэтому получить их полное описание непросто.
В той степени, в какой это вообще представляется возможным, это было сделано Е. М. Андреевым в 1970 году. Он доказал общую теорему, относящуюся не только к многогранникам Кокстера, но и ко всем выпуклым многогранникам, двугранные углы которых не превосходят π/2. Такие многогранники называются остроугольными (хотя они могут иметь и прямые двугранные углы). Как мы доказали в разделе 4 (доказательство не изменяется в случае пространства Лобачевского), всякий остроугольный многогранник является простым.
Теорема Андреева дает необходимые и достаточные условия существования в пространстве Лобачевского остроугольного многогранника заданного комбинаторного строения, отличного от треугольной пирамиды, с заданными двугранными углами. Эти условия суть следующие:
- если какие-либо три грани сходятся в одной вершине, то сумма углов между ними больше π (необходимость этого условия была доказана в разделе 4);
- если какие-либо три грани попарно смежны, но не сходятся в одной вершине, то сумма углов между ними меньше π;
- если какие-либо четыре грани смежны «по кругу» (как боковые грани четырехугольной призмы), то не все углы между ними равны π/2;
- если многогранник является треугольной призмой, то не все углы, образуемые основаниями с боковыми гранями, равны π/2.
Теорема Андреева в некотором смысле аналогична знаменитой теореме А. Д. Александрова о существовании евклидова многогранника с данной разверткой. Однако ее точного аналога в евклидовой геометрии нет (и не может быть). Это одна из специфических теорем геометрии Лобачевского, подобно признаку равенства треугольников по трем углам.
С помощью теоремы Андреева нетрудно, например, доказать существование в пространстве Лобачевского «прямоугольных» многогранников (т.е. многогранников, все двугранные углы которых прямые) со сколь угодно большим числом граней. (Читатель вполне может сделать это самостоятельно.) Тем самым получим много разнообразных прямоугольных калейдоскопов в пространстве Лобачевского. Не имея возможности обсуждать это подробнее, заметим только, что начиная с конца прошлого века калейдоскопы в пространстве Лобачевского применялись к арифметике квадратичных форм, а в последние 15 лет они получили применение в трехмерной топологии.
Литература
1. Г. С. М. Кокстер. Введение в геометрию. М.: Наука, 1966.
2. Э. Б. Винберг, О. В. Шварцман. Дискретные группы движений пространств постоянной кривизны // Итоги науки и техники. Современные проблемы математики. Фундаментальные направления. М.: ВИНИТИ, 1988, т. 29.
3. Э. Б. Винберг. О неевклидовой геометрии // Соросовский образовательный журнал, 1996, № 3.
1 На сфере единичного радиуса. (Прим. ред.)
2 Матрица Грама семейства векторов образована их попарными скалярными произведениями. Если векторы линейно зависимы, то определитель матрицы Грама равен нулю. Подробнее о матрицах и определителях см., например, в учебнике Э. Б. Винберга «Курс алгебры» (М.: Факториал Пресс, 2001). (Прим. ред.)






























Рис. 1. Система из двух зеркал