Лев Шуткин,
кандидат технических наук
«Химия и жизнь» №3, 2006
- Паттерны — предшественники модулей
- Построение образующих
- Плетение модульных сетей
- Модульная химия
- Мир модулей
- Леонард Эйлер. Задача о кенигсбергских мостах
Плетение модульных сетей
В переносном смысле образующие — это логические узелки, которые позволяют сплести модульную сеть; при этом связи образующих попарно соединяются в сетевые связки. Такой способ соответствует широко распространенному в природе и обществе принципу попарного соединения выходов и входов модулей, из которых составляются модульные системы. Например, в нейросетях мозга этот принцип реализуется в синаптических соединениях типа «аксон-дендрит», в каждом из которых, как известно, участвует одно из многих аксонных окончаний одного нейрона и единственное дендритное начало другого. Шесть основных типов образующих в комбинации с другими типами порождают огромное множество модульных сетей, у которых возникают границы, где разворачиваются всяческие интересные события. Не секрет, что их описание служит источником головной боли для представителей самых разных наук; вспомним хотя бы афоризм Макса Планка: «поверхность придумал дьявол». Наглядно показать границы сетей и дать механизм рассмотрения этих событий — одна из задач теории модулей.
Сеть из двух линейных образующих
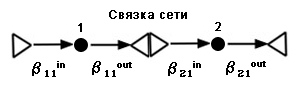
Простейшая ориентированная модульная сеть состоит из двух линейных образующих. При этом выходная связь первой образующей и входная связь второй соединены в связку; на схеме ее изображают двумя стрелками и ромбом, разделенным линией на два треугольника. Такая сеть может служить, например, моделью двух смежных блоков некоей компьютерной программы. Тогда две входные связи образующих представят данные на входах программных модулей, а две выходные связи — данные на их выходах.
Каждой связи образующей нужно сопоставить ее переменную. На рисунке они обозначены как β11in и β21in для входных связей и β11out и β21out для выходных связей. Если значения, присвоенные этим переменным, удовлетворяют условию соединения, то связка будет замкнута. В противном случае она разомкнётся.
Ребро графа, которое нельзя разорвать
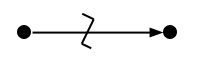
Модульную сеть можно преобразовать в графовую: для этого нужно свернуть ее связки по определенному правилу в графовые ребра и уничтожить внешние связи, если они есть. Если же внешние связи сохранить, то из модульной сети получится модульно-графовая. Более того, теория модулей обеспечивает единый математический аппарат описания модульных, графовых и табличных моделей данных. Особый интерес представляет применение модульно-графовых сетей к моделированию объектно-ориентированных и аспектно-ориентированных компьютерных программ.
10
Показать комментарии (10)
Свернуть комментарии (10)
-
Чесно говоря, абсолютно непонятно, чем предложеный подход отличается, например, от UNL или просто блок-схем в программировании. Тоесть эти принципы появились вместе со структурным программированием и получили развитие в объектно-ориентированых языках.
Правда, другое дело, что не всем абстрактное мышление привычно.-
1. Замечание Vego несомненно полезно, поскольку ставит вопрос о перспективах применения модульных сетей к компьютерному программированию.
2. Нельзя согласиться с утверждением Vego, что модульные сети и парадигма модульного мышления не представляют интереса, поскольку существуют UNL , стуктурное и объектно-ориентированное программирование. Обратите внимание, что сам Vego опровергает это утверждение своей последней фразой..
3. Замечание Vego, что структурное и объектно-ориентированное программирование исключают потребность в модульных сетях и парадигме модульного мышления спорно. Дело в том, что структурное и объектно-ориентированное программирование являются важными, но уже пройденными этапами развития технологий программирования. Сегодня быстро набирает силу новая технология аспектно-ориентированного программирования. Она основана на модульном подходе к проектированию программ. Для математического описания и наглядного представления аспектно-ориентированных программ могут быть применены модульные сети. Об аспектно-ориентированном программировании вы можете узнать на сайте www.javable.com/columns/aop.
4. Вопрос о соотношении языка UNL (Unified Network Language), упомянутого в замечании Vego, с языком теории модулей, позволяющим математически описывать модульные системы, требует специального исследования. UNL - это язык, предназначенный для отображения естественного английского языка в искусственный язык, понятный компьютеру. Язык UNL относится к области лингвистики. Теория паттернов Гренандера и связанные с ней теория модулей и модульные сети могут быть применены к решению задач математической лингвистики. Об использовании теории паттернов в лингвистике вы можете узнать из работ Ульфа Гренандера.
5. Оценивая практическую и теоретическую пользу модульных сетей и основанной на них парадигмы модульного мышления следует учитывать, что они имеют очень широкую сферу применений. Исследования показали, что модульные сети описывают структуры и содержания компьютерных гипертекстов и веб сайтов более детально чем графы. Они помогают проектировать учебные веб курсы и обучать студентов основам построения математических и визуальных моделей информационных систем и компьютерных программ. Теория модулей и парадигма модульного мышления позволяют совершенствовать терминологию в области информационных технологий. Модульные сети можно использовать в целях проектирования бюджетных систем, создания метода модульной декомпозиции сложных информационных систем, дополнения языка UML (Unified Modeling Language) модульными диаграммами и в ряде других областей знаний. Например, в статье Шуткина Л.В., помещенной на сайте www.elementy.ru, модульные сети описывают химические молекулы, как модульные системы с попарно сцеплеными валентностями атомов. В заметке Комарова С.М., дополняющей статью Шуткина, показано, что с помощью модульных сетей, описывающих помимо валентных и электрические сцепления атомов (силы Ван-дер-Ваальса) в молекулах изящно решается задача окисления угарного газа на кластере золота при участии воды. Важно подчеркнуть, что Комаров решил задачу используя лишь наглядные рисунки модульных сетей не прибегая к их математическому представлению. Предварительный анализ показал, что модульные сети можно применить к описанию влияния на работу головного мозга человека различных химических медиаторов. Значительный интерес представляет применение модульных сетей к инженерному проектированию развивающихся информационных систем министерств, агенств и субъектов Российской Федерации.
В заключение привожу перечень статей о теории модулей, модульных сетях и парадигме модульного мышления, намеченых к последовательному размещению на сайте www.morepc.ru в разделе 'Моделирование информационных систем и процессов' - http://www.morepc.ru/informatisation/articles.html?cat=89 :
1. 'Анализ теории модулей с помощью метафоры Холтона'.
2. 'Математическое единство модульных, графовых и табличных
моделей данных'
3. 'Кому и зачем нужны модульные сети'
4. 'Сходство и различие модульных и графовых сетей'
5. ' Математические и визуальные модели информационных систем'
6. ' Модульный взгляд на химию мозга'
7. ' Модульная декомпозиция развивающихся информационных
систем'.
8. ' Модульный взгляд на бюджетные системы'
9. 'Понятие информационная технология в законодательных актах и
бюджетных системах'
10. ' Классификация и кодирование информационных технологий в
бюджетных системах'.
Помощь в применения модульных сетей к практике вы можете получить у Шуткина Льва Владимировича, E-mail: shutkin@pvti.ru, тел. 490 44 35.
-
"...Модулем называется объект реального мира, который его наблюдатель счел целесообразным представить в виде образующей и использовать ее в качестве модели этого объекта."
Кто-нибудь может ответить, чем объект отличается от модуля? Зачем вводится еще одна сущность? Если есть объект и есть модель объекта.
Кто-нибудь может ответить, чем объект отличается от модуля? Зачем вводится еще одна сущность? Если есть объект и есть модель объекта.
-
Когда вы имеете дело с термином и его определением (понятием), то всегда должны помнить, что данное определение справедливо только в рамках некоторого контекста. За его пределами это определение обычно неверно. Например, определение термина 'вершина' в рамках теории графов означает точку, произвольно расположенную на плоскости или в ином пространстве. А в географии термин 'вершина' означает верхнюю часть горы.
В рамках теории модулей понятие 'объект' является более общим, чем понятие 'модуль', определяемое 'наблюдателем' в виде модели, называемой 'образующая'. В рамках теории модулей образующую, наряду с определением, приведенным в статье 'Парадигма модульного мышления' и повторенного в комментарии 'КАК', можно также определить, как объект, имеющий входы и/или выходы.
Например, наблюдатель рассматривая срез ткани мозга, окрашенный по методу У. Науты видит входные и выходные волокна тела нейрона, и может описать нейрон с помощью образующей, имеющей входы и выходы. Рассматривая окно рабочего стола системы Windows наблюдатель видит окно в целом и расположенные в нем пиктограммы (иконки). Хотя наблюдатель непосредственно не видит вход в окно и его выходы, связывающие пиктограммы с их функциональными окнами, он может мысленно представить вход и выходы окна и представить функциональный стол в виде образующей, имеющей один вход и несколько выходов, число которых равно числу пиктограмм. В результате такого подхода удалось построить модульные модели, представляющие компьютерные гипертексты более детально чем графовые сети. В виде образующей (модуля) можно представить организацию, обменивающуюся информацией с другими организациями. Такое модульное представление организаций позволяет решать задачи стандартизации их внешних электронных профилей. Ваш домашний телефон с помощью образующей может быть представлен, как модуль, потенциально соединенный мировой телефонной сетью со всеми другими телефонами мира.
О наблюдателях теории модулей, а также об ее идеях, принципах и языке вы можете узнать в статье 'Анализ теории модулей с помощью метафоры Холтона', которая будет помещена на сайте www.morepc.ru примерно через месяц в соответствующем подразделе 'Моделирование информационных систем и процессов' раздела 'Проблемы информатизации' - http://www.morepc.ru/informatisation/
Кстати, там же можно ознакомиться и с различными представлениями терминологии в сфере ИТ.-
Для Lev:
Я попробовал разобраться с приведенной Вами терминологией (толковый словарь), но, к сожалению, наткнулся на ряд трудностей в части терминов:
- данные это информация;
- информация это сведения или знания;
- сведения это события;
- событие это одномоментное идентифицируемое изменение состояния некоторой системы;
- знания, система, изменение, модуль - не определены;
- идентификация это присвоение субъектам или объектам доступа идентификатора и (или) сравнение предъявляемого идентификатора с перечнем присвоенных идентификаторов;
- объект это общий термин, которым обозначается любая индивидуально выделяемая сущность. Предмет или явление, которому можно присвоить название
Из этого набора получается, что данные = информация = сведения = события, при этом не указано, кто идентифицирует и в какой системе происходит изменения, в идентифицируемой или идентифицирующей? Кроме того, цепочка обрывается, так как нет определения некоторых терминов (знания, система, изменение.)
-
"теория модулей" - Новая парадигма Нового мировоззрения Нового тысячелетия - Древняя Философия Вечных Цивилизаций - ДФ ВЦ. (Гуглим)
"модульные сети" - вечная и бесконечная Паутина из так называемых вечных цивилизаций, которые могут породить и отремонтировать эту Паутину. Развитие цивилизации есть развитие феномена сознания. Предел развития всех цивилизаций есть Осознающий Бог.
"модульные сети" - вечная и бесконечная Паутина из так называемых вечных цивилизаций, которые могут породить и отремонтировать эту Паутину. Развитие цивилизации есть развитие феномена сознания. Предел развития всех цивилизаций есть Осознающий Бог.
Газета «Все для учителя», №7, март 2001 г., Украина
Замкнутые линии
…Когда я учился в институте, на одном из занятий заметил, что мой сосед занимается интересным делом — он вместо того, чтобы внимательно слушать преподавателя, настойчиво что-то вырисовывал. В тетради был нарисован прямоугольник, разделенный, на пять более малых (рис.1). Он поставил перед собой задачу провести непрерывную черту так, чтобы она проходила не более одного раза через все отрезки, которые соединяют вершины прямоугольников. Повторил несколько раз, и его попытки остались напрасными. Попробовал и я, иногда казалось — все, решение есть, и при проверке находился отрезок, который не был пересечен, или линия его пересекала дважды. Проходило время. Иногда вспоминалась задача, снова пытался решить, но результата не было.
Решил упростить рисунок, отбросил один отрезок, второй, нарисовал несколько различных фигур. Заметил, что в некоторых случаях непрерывную линию можно замкнуть саму на себя, в некоторых — нет, можно провести не одну замкнутую черту, а несколько (рис.2).
Со временем возникла закономерность.
Задача имеет решение в двух случаях:
1. При обведении отрезков фигуры замкнутыми линиями, все линии будут замкнутыми.
2. При обведении, одна линия останется незамкнутой (то есть ее невозможно замкнуть, не нарушая условия задачи).
Задача не имеет решения, если остается более, чем одна незамкнутая линия.
После такого вывода, замкнутые линии представляются как части непрерывной линии, а концы незамкнутой — как ее концы. Потому, когда появляются две незамкнутых линии, выходит, что мы прервали непрерывную линию, что противоречит условию задачи.
В литературе и в периодических изданиях, где предлагаются задачи на смекалку, встречается много задач данного типа (задачи на прохождение комнат, на обхождение территорий соединенных мостами, рисования фигур одним росчерком). Любую задачу вы можете решить, используя предложенный метод.
Первым, кто к подобным задачам применил математическое обоснование, был великий немецкий ученый Леонардо Эйлер. В 1736 г. он задумался над любопытной задачей: «На реке Прегель, где стоит город Кенигсберг, остров, правый берег, левый и территории соединенные семью мостами. Можно ли пройти по всем семи мостам, не ступив ни на один из них дважды», Эйлер решил задачу, ответ вышел отрицательным.
Докажем возможность использования метода замкнутых линий на выше упомянутой задаче. Для облегчения размышлений введем такие условные обозначения. Пусть A, B, C и D (рис.3) будут различные части суши, разделенные рукавами реки. Переход с места A в место B мы будем помечать через AB — все равно, по какому бы мосту мы не шли, по а или b. Если потом с B мы перейдем в D, то этот путь мы обозначим через ABD, так что здесь B однозначно означает и место пребывание и место отправления.
Перейдем с места A в место B по мосту а, затем вернемся с B в A по мосту b, прошли путь ABA, то есть вернулись в место, с которого начинали. За условием задачи: мосты пересекать разрешено только один раз, следовательно дальше пользоваться ими запрещено, вообразим, что они отсутствуют. Таким же подобным образом поступим с мостами c и d. По какому б из путей ABACA, ACABA, CABAC, BACAB мы не перемещались, во всех случаях возвращаемся на место с которого начинали, образовывая замкнутую линию.
Дальше продолжать движение можно с любого места A, B или C, нужно для этого начинать обход мостов а, b, c, d. (Замкнутой линией можно обвести по два моста а, b и с, d или все четыре). При обходе мостов а, b, c, d путь обозначался, пятью буквами. То есть, если мосты обходить по одному разу, то путь должен обозначатся (n+1), где n — количество пройденных мостов (при прохождении мостов а, b, c — путь обозначался ABAC). Местность D сообщается с местностями C, A, B соответственно мостами g, e, f. Начнем обход с A, то есть запишем ADB, но для обхода моста g, нужно запись дополнить DC, в целом — ADBDC. В записи появляется дополнительная буква, что противоречит условиям, при которых делался обход мостов. То есть, для прохождения моста g, один из мостов (e или f) пересекался дважды, или перешли реку (по воде), что запрещено условием задачи. Следовательно, невозможно пройти по всем семи мостам, не ступив ни на один из них дважды.
Негативный результат получим также при доказывании задачи по рис.1.
При использовании замкнутых линий, получаем не только ответ на вопрос, а наглядно видим очерки будущего пути. Пользуясь данным методом, не нужно блуждать по мостам и комнатам, не нужно знать понятие «графа» и разницу между четными и нечетными числами, нужно понимать условие задачи и хорошо держать в руке карандаш. То есть, младшие школьники смогут не только найти решение задачи и его обосновать, но и составлять их сами, над которыми будут долго думать взрослые.
В.Д. Жила, г. Овруч, Житомирская обл.
Замкнутые линии
…Когда я учился в институте, на одном из занятий заметил, что мой сосед занимается интересным делом — он вместо того, чтобы внимательно слушать преподавателя, настойчиво что-то вырисовывал. В тетради был нарисован прямоугольник, разделенный, на пять более малых (рис.1). Он поставил перед собой задачу провести непрерывную черту так, чтобы она проходила не более одного раза через все отрезки, которые соединяют вершины прямоугольников. Повторил несколько раз, и его попытки остались напрасными. Попробовал и я, иногда казалось — все, решение есть, и при проверке находился отрезок, который не был пересечен, или линия его пересекала дважды. Проходило время. Иногда вспоминалась задача, снова пытался решить, но результата не было.
Решил упростить рисунок, отбросил один отрезок, второй, нарисовал несколько различных фигур. Заметил, что в некоторых случаях непрерывную линию можно замкнуть саму на себя, в некоторых — нет, можно провести не одну замкнутую черту, а несколько (рис.2).
Со временем возникла закономерность.
Задача имеет решение в двух случаях:
1. При обведении отрезков фигуры замкнутыми линиями, все линии будут замкнутыми.
2. При обведении, одна линия останется незамкнутой (то есть ее невозможно замкнуть, не нарушая условия задачи).
Задача не имеет решения, если остается более, чем одна незамкнутая линия.
После такого вывода, замкнутые линии представляются как части непрерывной линии, а концы незамкнутой — как ее концы. Потому, когда появляются две незамкнутых линии, выходит, что мы прервали непрерывную линию, что противоречит условию задачи.
В литературе и в периодических изданиях, где предлагаются задачи на смекалку, встречается много задач данного типа (задачи на прохождение комнат, на обхождение территорий соединенных мостами, рисования фигур одним росчерком). Любую задачу вы можете решить, используя предложенный метод.
Первым, кто к подобным задачам применил математическое обоснование, был великий немецкий ученый Леонардо Эйлер. В 1736 г. он задумался над любопытной задачей: «На реке Прегель, где стоит город Кенигсберг, остров, правый берег, левый и территории соединенные семью мостами. Можно ли пройти по всем семи мостам, не ступив ни на один из них дважды», Эйлер решил задачу, ответ вышел отрицательным.
Докажем возможность использования метода замкнутых линий на выше упомянутой задаче. Для облегчения размышлений введем такие условные обозначения. Пусть A, B, C и D (рис.3) будут различные части суши, разделенные рукавами реки. Переход с места A в место B мы будем помечать через AB — все равно, по какому бы мосту мы не шли, по а или b. Если потом с B мы перейдем в D, то этот путь мы обозначим через ABD, так что здесь B однозначно означает и место пребывание и место отправления.
Перейдем с места A в место B по мосту а, затем вернемся с B в A по мосту b, прошли путь ABA, то есть вернулись в место, с которого начинали. За условием задачи: мосты пересекать разрешено только один раз, следовательно дальше пользоваться ими запрещено, вообразим, что они отсутствуют. Таким же подобным образом поступим с мостами c и d. По какому б из путей ABACA, ACABA, CABAC, BACAB мы не перемещались, во всех случаях возвращаемся на место с которого начинали, образовывая замкнутую линию.
Дальше продолжать движение можно с любого места A, B или C, нужно для этого начинать обход мостов а, b, c, d. (Замкнутой линией можно обвести по два моста а, b и с, d или все четыре). При обходе мостов а, b, c, d путь обозначался, пятью буквами. То есть, если мосты обходить по одному разу, то путь должен обозначатся (n+1), где n — количество пройденных мостов (при прохождении мостов а, b, c — путь обозначался ABAC). Местность D сообщается с местностями C, A, B соответственно мостами g, e, f. Начнем обход с A, то есть запишем ADB, но для обхода моста g, нужно запись дополнить DC, в целом — ADBDC. В записи появляется дополнительная буква, что противоречит условиям, при которых делался обход мостов. То есть, для прохождения моста g, один из мостов (e или f) пересекался дважды, или перешли реку (по воде), что запрещено условием задачи. Следовательно, невозможно пройти по всем семи мостам, не ступив ни на один из них дважды.
Негативный результат получим также при доказывании задачи по рис.1.
При использовании замкнутых линий, получаем не только ответ на вопрос, а наглядно видим очерки будущего пути. Пользуясь данным методом, не нужно блуждать по мостам и комнатам, не нужно знать понятие «графа» и разницу между четными и нечетными числами, нужно понимать условие задачи и хорошо держать в руке карандаш. То есть, младшие школьники смогут не только найти решение задачи и его обосновать, но и составлять их сами, над которыми будут долго думать взрослые.
В.Д. Жила, г. Овруч, Житомирская обл.
Написать комментарий
