Оловянные солдатики

Сначала оцените число передвигаемых солдатиков, докажите, что меньше нельзя, а затем придумайте пример передвижения солдатиков, удовлетворяющего условию задач.

Оценим число передвигаемых солдатиков. Заметим, что из любых двух солдатиков, которые в исходном каре стоят рядом друг с другом в одной «шеренге» или в одной «колонне», по крайней мере один при переходе к новому каре должен быть передвинут, поскольку расстояние между этими солдатиками должно увеличиться. А так как в исходном каре легко указать 40 попарно непересекающихся пар солдатиков-соседей (пример разбиения на пары показан на рис. 2), то передвинуть придется не менее 40 солдатиков.

Рис. 2.

Покажем, что построение большего каре можно выполнить перестановкой ровно 40 солдатиков. Для этого раскрасим точки в шахматном порядке в черный и красный цвета (рис. 3, слева). Переставлять будем красные точки (их 40), черные точки останутся на месте (их 41). Диагоналями квадрата разделим все красные точки на четыре множества (рис. 3, справа).

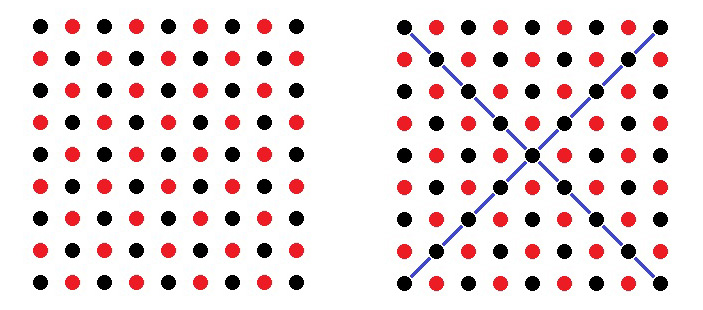
Рис. 3.

На рис. 4 слева черным кружочком выделено одно из четырех множеств, это нижняя четверть исходного каре — 10 красных точек. Стрелками указано направления для перемещения каждой из этих точек. Справа на рис. 4 показан результат этого перемещения. В результате передвижения красные точки опять «становятся» черными, то есть попадают на диагональные ряда из точек.

Рис. 4.

Если такие же перемещения проделать для других трех множеств, то получим новое каре. Оно квадратное, повернуто на 45°, и его размеры больше исходного в \(\sqrt2\) раз (рис. 5). При этом расположение поменяли ровно 4×10 = 40 солдатиков.

Рис. 5.

Как говорится, «всё начинается с малого!». Вот и эта задача появилась, как продолжение задачи, опубликованной в журнале Квантик (в №2 за 2016 год):

Задача. Шесть кузнечиков сидят в вершинах двух квадратов с общей стороной, как показано на рисунке. Три кузнечика прыгнули каждый на новое место, все прыжки были одинаковой длины. Могли ли после этого все шестеро кузнечиков вновь оказаться в вершинах двух квадратов с общей стороной другого размера?

Рис. 6.

Обозначая кузнечиков точками, приходим к решетчатым прямоугольникам. Исследуя в этом направлении точечные прямоугольники, в которых m и n точек на сторонах, обнаружены красивые перестроения точек в точечных квадратах с нечетным количеством точек на стороне. Оказалось, что квадратное каре, в котором \((2n+1)^2\) солдатиков можно «разредить», передвинув при этом ровно n солдатиков. Так появилась наша задача, приведенное решение для каре из 9² солдатиков обобщается для квадратного каре, в котором \((2n+1)^2\) солдатиков, потому что при любом натуральном n все шаги решения задачи можно повторить без ограничений.

В случае с каре, на сторонах которого четное число 2n солдатиков, задача решается передвижением ровно половины солдатиков. Чтобы это показать, снова раскрасим их в шахматном порядке. Понятно, что черных и белых солдатиков будет поровну (рис. 7). При перестановке черные солдатики останутся на своем месте, а все белые поменяют свое положение. Двумя синими отрезками множество, состоящее только из белых солдатиков, можно разбить на четыре блока треугольной формы. На рис. 7 они выделены треугольниками с закругленными углами. Остается только передвинуть эти блоки на новые места и перекрасить белые точки в черный цвет — при этом получится квадратное каре размером 2n×2n, в котором расстояние между соседними солдатами увеличилось в \(\sqrt2\) раз.

Рис. 7.

Перестроения прямоугольных каре тоже интересны, но общего подхода в этом случае найти не удалось — только для некоторых классов точечных прямоугольников удалось установить минимальное количество передвигаемых солдатиков-точек. Например, в прямоугольных каре размером \(n\times(n+1)\) наименьшим числом передвигаемых солдатиков тоже является n. Опять, если точки исходного черного прямоугольника \(n\times(n+1)\) раскрасить в шахматном порядке в черные и серые цвета, и наложить его на синий точечный прямоугольник, в котором расстояние между соседними точками в \(\sqrt2\) раз больше, то все точки исходного прямоугольника окажутся в синем прямоугольнике, кроме одной серой точки (рис. 8). Это происходит потому, что квадрат со стороной n полностью помещается в квадрате со стороной \(n\sqrt2\), а в этом случае одна сторона исходного прямоугольника на 1 больше.

Рис. 8.

Понятно, что исходное прямоугольное каре \(m\times n\), у которого длина \(m\) значительно больше ширины \(n\) (насколько больше, выясним чуть позже) могут иметь с каре, размеры которого в \(\sqrt2\) раз больше максимум \(n^2\) общих точек (черные на рис. 9), которые не передвигаются при построении. Это значит, что в этом случае придется передвигать \(mn-n^2\) серых точек-солдатиков.

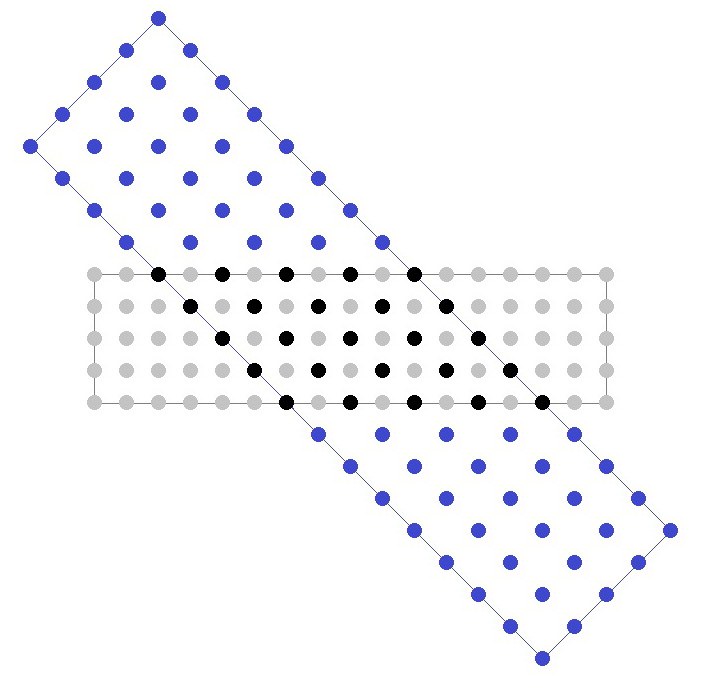
Рис. 9.

Каковы пределы размеров прямоугольного каре для случая «большой длины»? Самая маленькая длина, когда в пересечении черного и синего каре получается \(n^2\) общих точек, будет в том случае, когда две вершинные точки окажутся на сторонах синего прямоугольника (рис. 10). Если ширина черного прямоугольника в точках равна \(n\), то длина \(m=(2n-1)+(n-1)=3n-2\). В этом случае каре содержит \(n(3n-2)\) точек-солдатиков, а передвигать придется на \(n^2\) солдатиков меньше, то есть всего \(2n(n-1)\) штук.

Это значит, что если ширина исходного каре равна \(n\) в точках, а длина \(m\) больше, чем \(3n-2\), то при построении нового каре придется передвигать \(mn-n^2\) точек-солдатиков.

Промежуточные значения длины \(n+1<m<3n-2\) в общем случаи остались не изученными. Буду рад общению по этому вопросу, чтобы закрыть его.

Рис. 10.

И еще один интересный пример. Рассмотрим задачу для нахождения формулы «возвратной» суммы \(S_n\) первых нечетных чисел \(S_n=1+3+\ldots+(2n-1)+\ldots+3+1\). На первый взгляд, она никак не связана с нашей задачей и решать ее можно многими способами. Оказывается, использование рассмотренных выше приемов с «прореживанием» решетки, позволяет найти эту формулу буквально просто взглянув на картинку (рис. 11).

Рис. 11.

Во-первых, нетрудно убедиться, что число точек в таком «каре» как раз равно \(S_n\) потому что, если посчитать число точек косыми рядами, параллельными одной из диагоналей квадратного каре, то как раз и получим эту сумму. На рис. 11, показан пример для \(n=8\).

Во-вторых, число точек в таком «каре» можно посчитать иначе, если снова закрасить точки в шахматном порядке и вывести из каре синие точки, то получим два новых точечных квадрата, в которых \(n^2\) и \((n-1)^2\) точек соответственно (рис. 12). Значит, \(S_n= n^2 + (n-1)^2\).

Рис. 12.