Последовательности на спирали
Задача
Рассмотрим бесконечную клетчатую плоскость, в каждую клетку которой вписано натуральное число, — по порядку, начиная с 1, следуя по спирали (рис. 1). Спираль для определенности будем считать завивающейся по часовой стрелке.

Введем прямоугольную систему координат с началом в центре клетки с 1 и осями, параллельными сторонам клеток. Нарисуем параболу \(y=x^2\) и рассмотрим на ней точки с целыми координатами. Каждая такая точка определяет клетку плоскости и, как следствие, — написанное в ней число (см. рис. 1). Например, вершине параболы (0; 0) соответствует число 1, точке (1; 1) — число 9, а точке (2; 4) — число 79. Пусть \(a_n\) — число, соответствующее точке \((n;\,n^2)\) параболы; тогда \(a_0=1\), \(a_1=9\), \(a_2=79\), ... Найдите а) 4-й, б) 10-й, в) \(n\)-й члены последовательности \((a_n)\).
Подсказка
Представьте квадратную спираль как объединение вложенных друг в друга квадратных рамок. Выясните, какие числа спирали расположены в правом верхнем углу каждой рамки, а какие — в левом верхнем углу? Так можно добраться до чисел спирали, лежащих на оси \(y\), а там уж рукой подать до чисел спирали, расположенных в целочисленных точках правой ветви параболы.
Решение
Отрезки чисел натурального ряда [2; 9], [10; 25], [26; 49], ... образуют витки спирали, располагаясь в квадратных рамках. На рис. 2 белым и синим цветом выделены первые шесть рамок.

Рис. 2.
Рассмотрим один из витков спирали, например отрезок натурального ряда от 50 до 81, в котором находится второй член последовательности \(a_2=79\) (рис. 3). Как получить \(a_2=79\) не «графически», а «вычислительно»?
Поскольку это второй член последовательности и его определяет целочисленная точка (2; 4) параболы, то он находится в четвертой рамке, выделенной на рис. 3 зеленым цветом. Понятно, что эта квадратная рамка имеет размер 9×9 и в правом верхнем ее углу расположено число 81, а в левом верхнем углу расположено число \(73=81-(9-1)\). Тогда на пересечении этой стороны квадратной рамки с осью \(Oy\) расположено число 77, равное среднему арифметическому угловых чисел 81 и 73. Чтобы получить искомый член 79 остается к 77 прибавить 2 — номер этого члена последовательности.
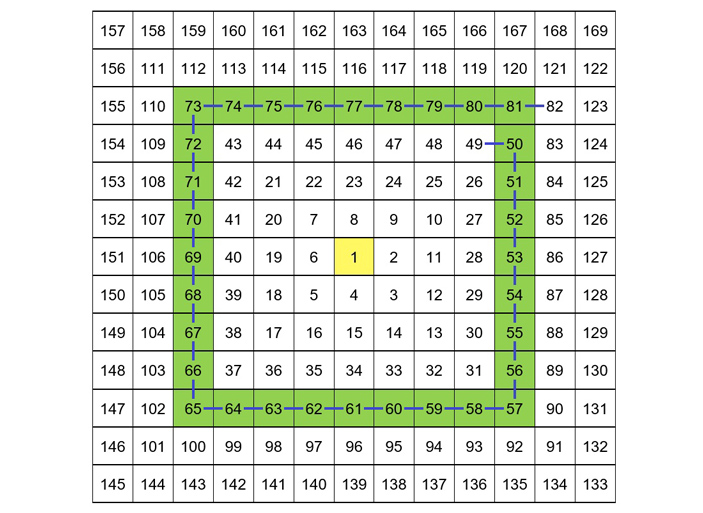
Рис. 3.
а) Чтобы найти четвертый член последовательности, поступим так же. Раз это четвертый член, то он определяется целочисленной точкой (4; 16), поэтому он расположен в 16-й квадратной рамке размером \(2\cdot16+1=33\). Значит, в правом верхнем углу рамки расположено число \(33^2=1089\), а в левом верхнем углу расположено число \(1089-(33-1)=1057\). В средней клетке верхней стороны рамки записано число \((1089+1057):2=1073\), поэтому \(a_4=1073+4=1077\).
б) и в) Далее можно обобщить этот прием и найти формулу n-го члена последовательности, и по ней вычислить \(a_{10}\). Проделаем это.
Число \(a_n\) определяется точкой \((n;\,n^2)\) параболы. Поэтому оно расположено в квадратной рамке с номером \(n^2\), размер которой равен \((2n^2+1)\times(2n^2+1)\). В правом верхнем углу этой рамки расположено число \((2n^2+1)^2\), а в левом верхнем углу расположено число \((2n^2+1)^2-2n^2\). В средней клетке верхней стороны рамки записано число, равное среднему арифметическому чисел, записанных на концах этой стороны, то есть \((2n^2+1)^2-n^2\). Чтобы найти \(n\)-й член последовательности, нужно серединное число увеличить на \(n\), получим \(a_n=(2n^2+1)^2-n^2+n\) или, если раскрыть скобки, \(a_n=4n^4+3n^2+n+1\).
Подставляя \(n=10\), получим \(a_{10}=40311\).
Послесловие
Имея формулу \(n\)-го члена последовательности, можно вычислить несколько ее первых членов: 1, 9, 79, 355, 1077, 2581, 5299, 9759, 16585, 26497, 40311, ... Оказалось, что этой последовательности не было в Онлайн-энциклопедии целочисленных последовательностей (OEIS) Нила Слоуна, хотя там хранится описание более 350 тысяч последовательностей.
Всех авторов, отправляющих свои последовательности на рассмотрение, предупреждают, что если они не хотят, чтобы страницу с их последовательностью многократно перекраивали, зачеркивали и добавляли фрагменты, то лучше не отправлять их в базу. Тем не менее, я добавил эту последовательность в OEIS. В течение месяца описание последовательности претерпело многократные изменения, которые вносили эксперты энциклопедии или я по их просьбе, но по прошествии периода редактирования последовательность одобрили и сейчас ее можно там найти под номером A357281. Мне особенно приятно, что заключительное одобрение сделал сам Нил Слоун.
Последовательность из нашей задачи определялась целочисленными точками правой ветви параболы \(y=n^2\), но целочисленные точки имеются и на левой ветви этой же параболы. Эти точки определяют новую последовательность, начало которой 1, 7, 75, 349, ... (рис. 4).

Рис. 4.
Формулу \(n\)-го члена второй последовательности легко найти. Для этого нужно повторить все шаги поиска формулы \(n\)-го члена первой последовательности, кроме последнего. Если в первой последовательности серединное число увеличивали на \(n\), то во второй последовательности серединное число нужно уменьшать на \(n\). В итоге получим: \(b_n=(2n^2+1)^2-n^2-n\) или \(b_n=4n^4+3n^2-n+1\). Вот 10 ее первых членов: 1, 7, 75, 349, 1069, 2571, 5287, 9745, 16569, 26479.
Но параболу с коэффициентом 1 можно разместить по-другому: ветвями вниз, влево и вправо. И в этих случаях целочисленные точки каждой полупараболы (коих всего восемь) будут определять еще шесть новых последовательностей (рис. 5).

Рис. 5.
Формулы n-х членов двух последовательностей уже найдены. Чтобы найти формулы остальных, вспомним задачу Две таблицы. Как вы заметили, в поиске формулы n-го члена первых двух последовательностей важную роль сыграло серединное число. А в этой задаче для каждой стороны k-й квадратной рамки серединные числа уже были найдены (рис. 6).
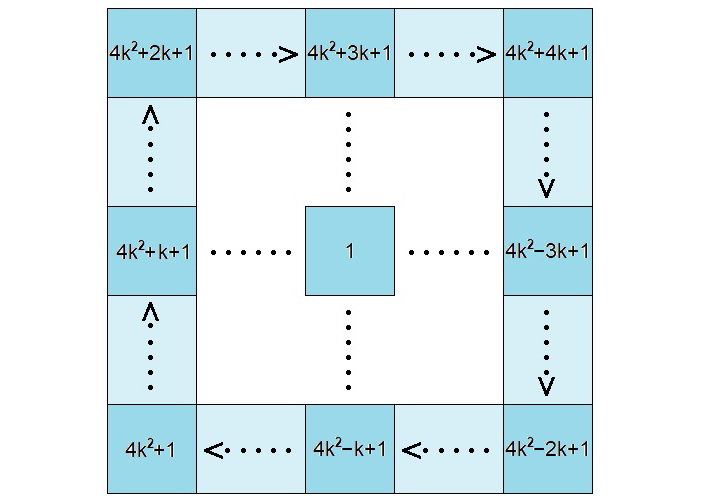
Рис. 6.
Учитывая, что в нашей задаче при поиске формулы n-го члена последовательностей речь идет о рамке с номером \(n^2\), нужно во всех формулах на рис. 6 число \(k\) заменить на \(n^2\), и прибавить или отнять число \(n\).
Проделаем это подробней для последовательностей (3) и (4) (см. рис. 5). Серединное число для этих полупарабол равно \(4n^4+n^2+1\). Числа спирали на этой стороне квадратной рамки возрастают сверху вниз, поэтому чтобы получить формулу n-го члена последовательности (3), нужно к этому серединному числу прибавить \(n\). Получим: \(a_n=4n^4+n^2+n+1\) (3). Вот десять первых ее членов: 1, 7, 71, 337, 1045, 2531, 5227, 9661, 16457, 26335, ....
Чтобы получить формулу n-го члена последовательности (4), нужно из серединного числа вычесть \(n\). Получим: \(a_n=4n^4+n^2-n+1\) (4). Вот десять первых ее членов: 1, 5, 67, 331, 1037, 2521, 5215, 9647, 16441, 26317, ....
Формулы n-го члена остальных четырех последовательностей находятся аналогично, просто приведем их и 10 первых членов этих последовательностей:
\(a_n=4n^4-n^2+n+1\), (5): 1, 5, 63, 319, 1013, 2481, 5155, 9563, 16329, 26173;
\(a_n=4n^4-n^2-n+1\), (6): 1, 3, 59, 313, 1005, 2471, 5143, 9549, 16313, 26155;
\(a_n=4n^4-3n^2+n+1\), (7): 1, 3, 55, 301, 981, 2431, 5083, 9465, 16201, 26011;
\(a_n=4n^4-3n^2-n+1\), (8): 1, 9, 51, 295, 973, 2421, 5071, 9451, 16185, 25993.
Любопытный момент: в последовательности (8) формула выдает все члены верно, кроме второго (соответствующего \(n=1\)): должно быть 9, а по формуле получается 1. Сможет ли кто-то из читателей объяснить этот эффект?
Последние задачи













Рис. 1.