Две таблицы

Начните с таблиц небольшого размера. Убедитесь, что утверждение задачи выполнено для таблиц 5×5, но не выполняется в таблицах 7×7. Попытайтесь выяснить, почему так происходит и для каких еще таблиц выполняется утверждение задачи.

Сначала посмотрим, какие клетки закрашены в первой таблице. Поскольку в каждой ее строке расположены последовательные натуральные числа, то закрашенные клетки — те, которые имеют номера, дающие при делении на 4 остаток 1, — отстоят друг от друга на три незакрашенные клетки. В первой строке, очевидно, закрашены 1-я, 5-я, 9-я, и так далее вплоть до последней клетки, которая тоже закрашена, потому что \(2021=4\times505+1\). Из-за этого во второй строке первые три клетки не закрашены, а закрашены 4-я, 8-я, ..., предпоследняя клетки. То есть во второй строке по сравнению с первой закрашена со смещением влево на одну клетку. Ясно, что такое же смещение закрашенных клеток влево на одну будет происходить в каждой следующей строке. Значит, закрашенные клетки будут выстраиваться вдоль равноотстоящих параллельных диагоналей таблицы (рис. 2).

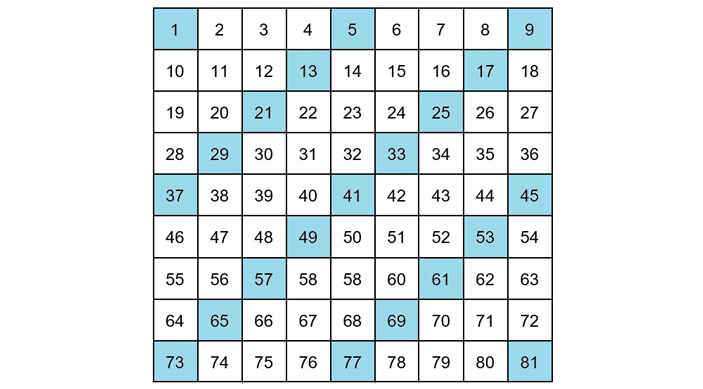
Рис. 2.

Теперь разберемся со второй таблицей, в которой клетки нумеруются по спирали, начиная с центральной. В ней можно выделить квадраты, центр которых совпадает с центром таблицы, а длина стороны нечетная. В таком квадрате со стороной \(2k+1\) находятся первые \((2k+1)^2\) натуральных числа (рис. 3, слева). Поэтому в правом верхнем углу каждого такого квадрата (там, где находится последнее из этих чисел) записаны квадраты нечетных чисел, дающие при делении на 4 остаток 1. В нижнем левом углу каждого квадрата записаны числа вида \(4k^2+1\), ведь чтобы «дойти» до него из правого верхнего угла, нужно «пройти» по верхней и левой стороне квадрата, посетив ровно \(4k\) клеток. Значит, мы уже знаем, что полностью закрашена главная диагональ таблицы (рис. 3, справа).

Рис. 3.

Теперь разобьем таблицу на квадратные рамки толщиной в одну клетку. Слева на рис. 4 они показаны белым и желтым. Мы уже знаем, что в каждой такой рамке правый верхний и левый нижний углы закрашены. А что с другой парой углов? Легко видеть, что у белых рамок, соответствующих четным \(k\), оба эти угла будут закрашены, поскольку в этом случае номера этих клеток тоже дают остаток 1 при делении на 4 (ведь от каждого из них до любого из первой пары углов ровно \(4k\) клеток по прямой). Аналогично показывается, что в желтых рамках правый нижний и левый верхний углы всегда не закрашены. Более того, в этих углах всегда находятся незакрашенные уголки из трех клеток (рис. 4, справа).

Рис. 4.

Раз углы всех белых рамок устроены одинаково и углы всех желтых рамок устроены одинаково, то при последовательном наращивании размера таблицы путем накладывания все более и более крупных рамок закрашенные клетки будут появляться единообразно: при добавлении очередной белой рамки в дело будет вступать очередная диагональ, которая по мере увеличения размера рамок будет закрашиваться. Все такие закрашенные диагонали отстоят друг от друга на три клетки, как и в первой таблице, а закраски совпадают (рис. 5).

Рис. 5.

Приведенное рассуждение, хоть и наглядное, не совсем строгое. Ниже — второе решение, лишенное этого недостатка.

Пусть \(n_{ij}\) — номер клетки, находящейся на пересечении \(i\)—й строки и \(j\)-го столбца (\(1\le i,\ j\le 2021\), строки нумеруются сверху вниз, а столбцы — слева направо). По условию в каждой из таблиц закрашены клетки, для которых \(n_{ij}\equiv1\ (\mathrm{mod}\ 4)\).

В первой таблице для \(1\le i,\ j\le 2021\) выполнены соотношения \(n_{ij}=2021(i-1)+j\equiv i-1+j\ (\mathrm{mod}\ 4)\), а потому условие закраски переписывается в виде \(i+j\equiv2\ (\mathrm{mod}\ 4)\).

Рассмотрим теперь вторую таблицу. Центральная клетка (\(i=j=1011\)), в которой записано число 1, закрашена, и для нее выполнено условие \(i+j\equiv2\ (\mathrm{mod}\ 4)\). Двигаясь по спирали, мы каждые четыре хода будем попадать в очередную закрашенную клетку (ходом называем переход из клетки с номером \(n\) в клетку с номером \(n+1\)). Докажем, что для каждой такой клетки будет выполняться указанное условие.

В самом деле, при движении слева направо или сверху вниз значение суммы \(i+j\) увеличивается с каждым ходом на 1, а при движении справа налево или снизу вверх — уменьшается на 1. Заметим также, что каждые два соседних звена спирали, при движении по которым происходит увеличение значение суммы \(i+j\), имеют равные длины, а отсюда следует, что длина каждого из промежутков возрастания этой суммы четна. Точно такой же вывод будет верным и в отношении промежутков убывания значения суммы \(i+j\). Поэтому номера всех клеток, являющихся концами промежутков монотонности, нечетны. А тогда для любой пары клеток с нечетными номерами, отличающимися на 2, значения суммы \(i+j\) также будут отличаться на 2.

Отсюда получаем, что для любой пары клеток с нечетными номерами, отличающимися на 4, значения суммы \(i+j\) либо будут равны, либо отличаются друг от друга на 4. Это и значит, что \(i+j\equiv2\ (\mathrm{mod}\ 4)\), если \(n_{ij}\equiv1\ (\mathrm{mod}\ 4)\).

Утверждение задачи справедливо для всех квадратов \(n\times n\), где \(n=4k+1\). Это легко показать с помощью математической индукции. Число 2021, очевидно, тоже относится к числам такого вида — для него \(k=505\).

Как ориентироваться в этих больших таблицах? Например, как определить местонахождение конкретного числа? На пересечении каких по счету горизонталей и вертикалей находится число, скажем, \(a=123456\)?

Для первой таблицы счет вертикалей удобно вести слева на право от 1 до 2021, а нумерацию горизонталей — сверху вниз от 1 до 2021. Учитывая принцип построения первой таблицы, для определения местонахождения этого числа в этой таблице достаточно число 123456 разделить на 2021 с остатком (рис. 6).

Рис. 6.

Неполное частное 61 указывает, что число 123456 находится на 62-й горизонтали, а остаток 175 показывает, что число 123456 находится на 175-й вертикали. И в общем виде: если натуральное число \(n\) из промежутка от 1 до 2021² представимо в виде \(n=2021k+r\), то в первой таблице оно находится на пересечении \((k+1)\)-й горизонтали и \(r\)-й вертикали. И обратно: на пересечении \(k\)-й горизонтали и \(r\)-й вертикали находится число \(2021(k-1)+r\).

Для определения местоположения чисел во второй таблице-спирали размером 2021×2021 полезно рассмотреть концентрические квадратные рамки (как в решении) и пронумеровать их числами от 1 до 1010. В рамке с номером \(k\) в клетке правого верхнего угла записано число \((2k+1)^2\), в диагонально противоположной от нее клетке — число \(4k^2+1\), в клетке левого верхнего угла записано среднее арифметическое этих двух чисел, равное \(4k^2+2k+1\). Поскольку числа в угловых клетках рамки образуют арифметическую прогрессию, то в клетке нижнего правого угла записано число \(2(4k^2+1)-(4k^2+2k+1)=4k^2-2k+1\).

Можно найти числа, записанные в средних клетках на каждой стороне рамки, — получится убывающая арифметическая прогрессия из восьми чисел: \(4k^2+4k+1\), \(4k^2+3k+1\), ... \(4k^2-3k+1\), где каждое следующее число на \(k\) меньше предыдущего (рис. 7, слева).

Рис. 7.

В этой таблице вертикали и горизонтали удобно нумеровать целыми числами. Будем считать, что начальная клетка с числом 1 является пересечением вертикали с номером 0 и горизонтали с номером 0, номера вертикалей возрастают слева направо, а номера горизонталей — снизу вверх. Тогда клетки таблицы будут иметь координаты как в обычной декартовой системе координат, — будем записывать их в виде пары чисел, причем указывать сначала номер вертикали, а затем номер горизонтали. Например, клетка с числом 44 будет иметь координаты (−2; 3), то есть она лежит на пересечении второй вертикали влево и третьей горизонтали вверх от начала отсчета.

Теперь можно определить координаты числа 123456. Квадратный корень из этого числа \(\sqrt{123456}\approx351{,}36\), поэтому ближайший «сверху» нечетный квадрат равен \(353^2=124609\). Это число правого верхнего угла той квадратной рамки, в которой находится число 123456. Ее номер \(k=176\) найдем из уравнения \(2k+1=353\). Восемь чисел этой рамки, про которые мы уже точно знаем, где они расположены, приведены справа на рис. 7.

Число 123456 попадает в промежуток от 123377 до 123553, поэтому оно находится в вертикали с номером 176. Учитывая, что 123377 находится на нулевой горизонтали, число 123456 находится в горизонтали с номером \(123377-123456=-79\), то есть на 79-й по счету горизонтали вниз от нулевой.

Отсюда вытекает простой алгоритм нахождения координат произвольного числа \(n\) в таблице-спирали:
    1) Определить номер \(k\) рамки, в которой находится число \(n\). Для этого нужно найти ближайший нечетный квадрат \(K\), превосходящий \(n\), и решить уравнение \(2k+1=\sqrt{k}\).
    2) Вычислить номера остальных углов этой рамки, а также определить номера середин ее сторон. Определить, на какой из получившихся восьми промежутком попадает число \(n\).
    3) Вычислить координаты числа \(n\) с учетом из знака.

Еще одно простое наблюдение про рассматриваемые таблицы: если раскрасить четные числа черным, а нечетные числа — белым, то обе таблицы будут раскрашены (естественно) в шахматном порядке, причем совершенно одинаково (рис. 8).

Рис. 8.

Изучая расположение различных подмножеств натуральных чисел в этих таблицах, можно обнаружить интересные находки. Читателям, возможно, известна скатерть Улама, в которой в таблице-спирали выделено подмножество простых чисел (рис. 9). Оказывается, что они имеют тенденцию выстраиваться вдоль диагоналей таблицы в довольно длинные ряды. Это хорошо видно, если рассмотреть увеличенный вариант рис. 9. У скатерти Улама есть разные вариации и обобщения, в которых проявляются необычные визуальные закономерности разных числовых множества. Узнать о них можно по приведенной ссылке. Рекомендуем также прочитать статью Ю. В. Матиясевича Формулы для простых чисел. Еще об одной интересной визуальной закономерности в распределении простых чисел, возникающей, если отметить каждое число \(n\) натурального ряда в точке с полярными координатами \((n,\;n)\) на координатной плоскости, и об ее связи с рациональными приближениями числа пи можно узнать из этого замечательного видео (есть русский перевод).

Рис. 9. Скатерть Улама. Изображение с сайта ru.wikipedia.org

Но наши находки связаны с треугольными числами. Не обнаружив закономерностей в первой таблице, где треугольные числа расположены практически хаотично, я перешел к таблице-спирали. Закрасив клетки с треугольными числами в квадрате 9×9 и не обнаружив ничего интересного, я все же решил сделать это на большем квадрате 49×49. Здесь стали вырисовываться спирали. Они явно стали проявляться на больших квадратах 101×101 и 201×201 (рис. 10). Такую же спиралевидность расположения точек можно увидеть и в таблице размером 2021×2021. Интересно было бы объяснить этот визуальный эффект.

Рис. 10.

Отрезки, соединяющие клетки в которых записаны соседние треугольные числа, задают самопересекающиеся ломаные. Ломаные, закручиваясь спирально, образуют красивые звездчатые формы (рис. 11). Можно обнаружить семейства отрезков, проходящих через одну точку. Объяснить этот факт мне не удалось.

Рис. 11.

Еще одно наблюдение. Разобьем множество треугольных чисел на три подмножества таким образом: в первое подмножество включим треугольные числа с номерами вида \(3k+1\), во второе подмножество — треугольные числа с номерами вида \(3k+2\), в третье подмножество — треугольные числа с номерами вида \(3k\). Если в каждом подмножестве чисел, отмеченных в таблице, соседние числа соединить отрезком, причем в каждом множестве своим светом, то получим три вложенные друг в друга спирали. На рис. 12 приведены примеры таких спиралей для таблиц 101×101, 149×149, 202×201 и 1001×1001.

Рис. 12.

Благодарю моего ученика Сергея Прику за помощь с подготовкой рисунков.