Магия спирографа

Основную информацию для решения надо «выуживать» из картинок. В первую очередь нужно разобраться в движении подвижного диска и понять, какие виды вращения он совершает и сколько делает оборотов до возвращение в исходное положение.

Приведем общие рассуждения, работающие для всех трех случаев.

Пусть \(N\) — число зубьев на внутренней стороне отверстия, \(n\) — число зубьев на подвижном диске. Заметим, что по мере своего движения подвижный диск совершит несколько оборотов вокруг своего центра и вновь окажется в исходном положении, а вычерчиваемая при этом кривая замкнется. Здесь надо различать два вида оборотов. Во-первых, движение подвижного диска можно рассматривать как его перемещение по внутренней стороне отверстия. Число совершенных при этом оборотов обозначим \(K\). Во-вторых, движение диска можно рассматривать как его вращение относительно центра отверстия. Число совершенных при этом оборотов обозначим \(k\).

Очевидно, что, если диск после нескольких оборотов оказался в исходном положении, то выполняется соотношение: \(Nk =nK\).

Рассмотрим пример. Пусть \(N=96\), а \(n=32\) (рис. 3). Подвижный диск в начальном положении касается отверстия в точке A. Будем следить за траекторией этой точки диска. При перемещении диска по внутренней стороне отверстия (красная окружность на рис. 3) она описывает дугу \(AB\), потом дугу \(BC\), а затем дугу \(CA\). После этого она вернется в исходное положение. При этом диск совершил \(K=3\) оборота, катясь по красной окружности, но вокруг центра он сделал \(k=1\) оборот, то есть \(96\times1=32\times3\).

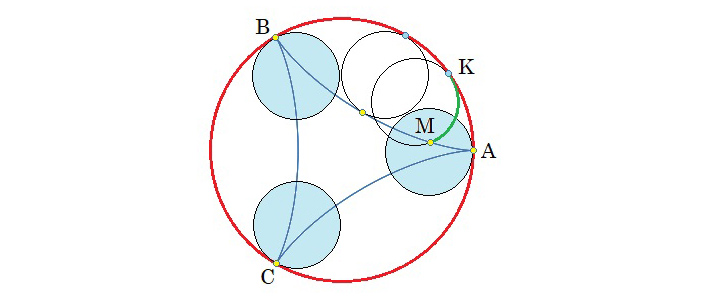
Рис. 3.

Как определять числа \(K\) и \(k\) по изображению гипотрохоиды? Нетрудно понять, что \(K\) равно количеству точек гипотрохоиды, максимально удаленных от ее центра. А чтобы определить число \(k\), можно из центра гипотрохоиды провести любой луч, — тогда \(k\) равно количеству точек пересечения этого луча с гипотрохоидой (важное замечание — нужно учитывать кратности точек пересечения, потому что луч может пройти через точку, в которой гипотрохоида пересекает сама себя).

Теперь перейдем к решению задач из условия. В каждой из них можно определить число \(n\), воспользовавшись равенством \(Nk =nK\).

а) На рис. 4 слева показано, что данная гипотрохоида имеет восемь максимально удаленных от ее центра точек, значит, \(K=8\). Эти точки занумерованы в порядке их появления при построении гипотрохоиды. Справа на рис. 4 показано, что произвольный луч, выходящий из центра гипотрохоиды пересекает ее трижды, то есть \(k=3\). Учитывая, что по условию \(N=96\), получаем, что на диске 36 зубьев.

Рис. 4.

б) Этот пункт решается аналогично. Как видно из рис. 5, гипотрохоида имеет 24 максимально удаленных точки, а значит, \(K=24\). Справа на рис. 5 показан луч, выходящий из центра гипотрохоиды и пересекающий ее в трех точках. Но две из них «двойные» — они являются точками самопересечения гипотрохоиды. Поэтому \(k=5\). В итоге получаем, что диск содержит \(n=\frac{Nk}{K}=\frac{96\cdot5}{24}=20\) зубьев.

Рис. 5.

в) Конечно, и в этом пункте задачу можно решить таким же способом. Но существует другой прием. Обсудим его.

Данная гипотрохоида на окружности с 96 зубьями имеет 24 «лепестка», поэтому между вершинами соседних лепестков помещается \(96:24=4\) зуба (рис. 6, слева). Проследовав по «красному» участку гипотрохоиды (рис. 6, справа) от вершины одного «лепестка» до вершины другого (это соответствует одному обороту диска по внутренней стороне окружности), найдем, что диск «прокатывается» по 11 таким промежуткам по 4 зубца в каждом. Значит, на нем \(11\times4=44\) зуба.

Рис. 6.

Какими формулами задаются эти красивые линии, которые рисует спирограф? Рассмотрим сначала частный случай, когда «рисующая» точка \(M\) подвижного диска находится на окружности этого диска (рис. 7, слева).

Рис. 7.

Количества зубцов на отверстии и на диске непосредственно связаны с длинами этих окружностей, а длины окружностей пропорциональны их радиусам, поэтому далее в качестве параметров окружностей будем использовать их радиусы \(R\) и \(r\).

В исходном положении точка \(M\) совпадает с точкой \(A\) оси \(Ox\). Положение подвижного диска можно определять его точкой касания с «красной» окружностью. В качестве параметра будем использовать угол \(t\), равный углу \(AOB\), выраженному в радианах. Если диск «прокатится» по внутренней стороне «красной» окружности из положения \(A\) в положение \(B\), то точка \(M\) нарисует дугу \(AM\) гипотрохоиды, причем дуги \(AB\) и \(BM\) окружностей равны. Но \(\overset{\LARGE{\frown}}{AB}=Rt\), \(\overset{\LARGE{\frown}}{BM}=\alpha r\), поэтому \(Rt=\alpha r\), значит, \(\alpha=\frac{Rt}{r}\).

Пусть точка \(M\) имеет координаты \(M(x;y)\), тогда \(x=OE+EK\). В прямоугольном треугольнике \(OEC\) найдем \(OE=OC\cos t=(R-r)\cos t\), в прямоугольном треугольнике \(CFM\) найдем \(FM=CM\sin\angle FCM\). Выразим \(\angle FCM\) через радиусы \(R\) и \(r\) и параметр \(t\): \(\angle FCM=\pi-\alpha-(\frac{\pi}{2}-t)=\frac{\pi}{2}-(\alpha-t)\). Учитывая, что \(\alpha=\frac{Rt}{r}\), получим \(\angle FCM=\frac{\pi}{2}-(\frac{Rt}{r}-t)\), но тогда \(FM=CM\sin\left(\frac{\pi}{2}-(\frac{Rt}{r}-t)\right)=r\cos(\frac{Rt}{r}-t)\). Значит, абсцисса текущей точки \(M\) равна \(x=(R-r)\cos t+r\cos(\frac{Rt}{r}-t)\).

Далее, \(t=MK=CE-CF\). В прямоугольном треугольнике \(OEC\) найдем \(CE=OC\sin t=(R-r)\sin t\), в прямоугольном треугольнике \(CFM\) найдем \(CF=CM\cos\angle FCM=r\cos\left(\frac{\pi}{2}-(\frac{Rt}{r}-t)\right)=-r\sin(\frac{Rt}{r}-t)\). Значит, ордината текущей точки \(M\) равна \(y=(R-r)\sin t-r\sin(\frac{Rt}{r}-t)\).

Таким образом, мы получили параметрическое уравнение гипотрохоиды в том случае, когда «рисующая» точка \(M\) подвижного диска находится на окружности этого диска:

Гипотрохоиду в этом случае называют гипоциклоидой. Например, в пункте б) данной задачи мы как раз имели дело с гипоциклоидой.

Рассмотрим теперь случай, когда «рисующая» точка \(M\) является внутренней точкой радиуса \(CN\) подвижного диска (рис. 7, справа). Пусть точка \(M\) находится от центра \(C\) этого диска на расстоянии \(d\). Пусть диск прокатился по дуге \(AB\), тогда точка \(M(x;y)\) опишет дугу \(DM\) гипотрохоиды. Проведя практически аналогичные рассуждения, можно показать, что координаты точки \(M\) таковы:

Итак, мы получили параметрическое уравнение гипотрохоиды в общем случае. Если сравнить параметрические формулы в обоих случаях, то с удивлением заметим, что уравнения почти идентичны: они отличаются лишь заменой радиуса \(r\) на расстояние \(d\). Но если немного задуматься, то ясно, что при \(d=r\) уравнения должны совпасть.

Как изменяется форма гипотрохоиды в зависимости от расстояния \(d\), показано на рис. 8. На нем приведено шесть гипотрохоид, нарисованных при помощи спирографа со следующими параметрами: на внутренней стороне отверстия 105 зубьев, на подвижном диске 75 зубьев. Расстояние \(d\) при рисовании изменялось от 0 до 75 с шагом 15. При \(d=0\) получилась окружность, при \(d=75\) — гипоциклоида.

Рис. 8.

Если все эти линии совместить так, чтобы их центры совпадали, не меняя при этом их ориентации, то получится красивая семиугольная розетка, в которой окружность постепенно трансформируется в гипоциклоиду по правилам спирографа (рис. 9).

Рис. 9.

Учитель физики из Иркутской области Наталья Менгали сконструировала прибор, который рисует гипотрохоиды лазером на экране. В основу которого положена обычная лазерная указка и два зеркала. Схема прибора изображена на рис. 10.

Рис. 10.

Луч лазера направляется на зеркало, которое прикреплено к оси вращения первого двигателя Д1. Отразившись от него, луч попадает на вращающееся зеркало второго двигателя Д2, а отразившись от него — на экран. Лазер и зеркала расположены так, что углы падения и отражения луча от зеркал близки к 45°. Если все эти углы будут в точности равны 45°, то луч будет отражаться в одну и ту же точку, — это неинтересный случай. Но если зеркала крепить к осям двигателя так, чтобы угол между осью двигателя и плоскостью зеркала отличался от прямого на 1–2 градуса, то при вращении зеркал они будут «вибрировать», и луч будет отображаться в разные точки экрана, рисуя на нем замысловатые кривые. Если менять скорости вращения зеркал, то можно получать кривые, похожие на гипотрохоиды, — получается лазерный спирограф. Инструкцию по сборке такого спирографа можно найти здесь.

Спирограф был изобретен в 1962 году английским инженером Денисом Фишером как прибор для черчения плавных линий. Инженерному сообществу спирограф не приглянулся, но понравился его детям. И Фишер организовал выпуск спирографа в качестве детской игрушки. Решение оказалось удачным — в 1967 году спирограф Фишера был назван игрушкой года в Великобритании. Действительно, это хорошая развивающая игрушка с интересным математическим содержанием. Как утверждают педагоги и психологи, спирограф развивает воображение, фантазию, творческое и логическое мышление, моторику рук. Надо сказать, что и взрослые используют спирограф — в том числе и для творчества: см., например, картины Мэри Вагнер.

Посмотрите на разнообразие гипотрохоид, которые задаются всего тремя параметрами \(R-r-d\). Именно в таком порядке они подписаны на рис. 11.

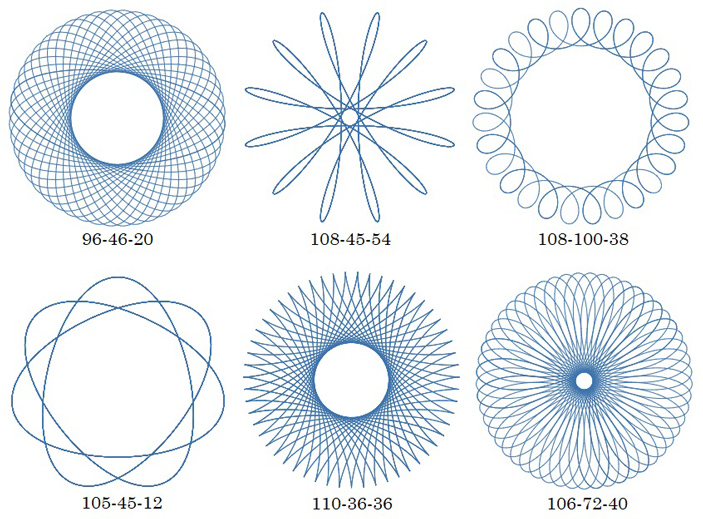
Рис. 11.

Автор благодарит Владимира Баталия, разработавшего графический редактор Spiro, при помощи которого были подготовлены рисунки.