Семь сот

Попробуйте сначала решить какую-нибудь одну из этих семи задач. На взгляд автора проще всего та, которая расположена в центре рисунка. Вам поможет свойство средней линии треугольника.

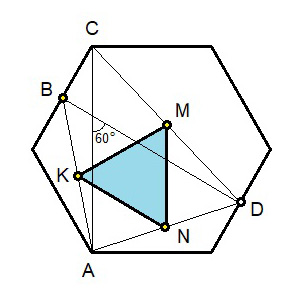
Рис. 2.

Сначала разберем самую простую из этих задач — на мой взгляд это центральный шестиугольник. Проведем отрезки AC и BD (рис. 2). Они равны, как расстояния между противоположными сторонами правильного шестиугольника, а угол между ними равен 60°. В треугольнике ABD отрезок KN является средней линией, а в треугольнике ACD средней линией является отрезок MN. Теперь можно воспользоваться свойством средней линии треугольника: она параллельна стороне треугольника, с которой не имеет общих точек, и равна ее половине. Отсюда следует, что KN = MN и угол между этими средними линиями равен 60°. Из этого вытекает, что треугольник MNK — равносторонний.

С одной задачей разобрались, но осталось еще шесть. Можно, конечно, каждую из них решать отдельно, но есть общий подход ко всем задачам сразу. Он основан на следующем факте.

Полезный факт. Равносторонние треугольники ОАВ и OCD имеют общую вершину О. Точки М и L — середины сторон АВ и CD, точки К и N — середины отрезков AD и ВС. Тогда треугольники MNK и KLN — равносторонние (рис. 3).

Рис. 3.

Идея доказательства такая же, как в разобранной выше задаче. Докажем, например, что треугольник MNK — равносторонний. Проведем отрезки АС и BD. Тогда треугольники АОС и BOD равны по двум сторонам и углу между ними (АО = ВО, СО = DO, ∠АОС = ∠AOD + 60°= ∠BOD). Из равенства этих треугольников следует, что АС = BD и что треугольник ОАС при повороте вокруг точки О на 60° совместится с треугольником OBD. При таком повороте отрезок АС совмещается с отрезком BD, а значит угол между этими отрезками равен 60°. Остается применить свойство средней линии треугольника к отрезкам MN и МК (они являются средними линиями в треугольниках ABC и ABD с равными основаниями АС и BD соответственно) и получить, что они равны друг другу, а угол между ними равен 60°. Отсюда следует, что треугольник KMN равносторонний. Для треугольника KLN доказательство аналогично.

Как же этот факт помогает решать предложенные задачи? Рассмотрим снова уже решенную задачу. На рис. 4 слева изображено условие этой задачи. Правее показан такой же шестиугольник, разбитый на треугольные ячейки, в котором закрашены желтым два треугольника с общей вершиной. Нетрудно убедиться, что оба этих треугольника — равносторонние. Наложение отрезков из условия задачи на эту сетку показывает, что в этой ситуации можно применить доказанный выше факт, из которого следует, что синий треугольник равносторонний.

Рис. 4.

Остальные задачи решаются аналогично: нужно в каждом шестиугольнике выделить два правильных треугольника с общей вершиной и отметить середины отрезков, соединяющие пары их вершин. Как это сделать, показано на рис. 5.

Рис. 5.

Доказанный нами полезный факт о свойстве двух правильных треугольников с общей вершиной не всегда выручает. Например, в правильном шестиугольнике, изображенном на рис. 6 слева, все отмеченные точки тоже являются серединами проведенных отрезков, а вот доказать, что закрашенный треугольник равносторонний этот факт не поможет: не удается закрасить два равносторонних треугольника с общей вершиной так, чтобы оставшиеся их вершины были концами заданных в условии отрезков.

Рис. 6.

Но зато удается найти три треугольника с общей вершиной. Соединив их соседние вершины отрезками, отметим середины этих отрезков и получим треугольник, с которого начинали (показанный слева на рис. 6). Почему он равносторонний?

Ответ на этот вопрос дает очень симпатичное свойство трех равносторонних треугольников с общей вершиной (рис. 7): если треугольники OAB, OCD и OEF равносторонние и направление обхода их вершин одинаково, то треугольник MNK, вершины которого совпадают с серединами отрезков FA, BC и DE — равносторонний.

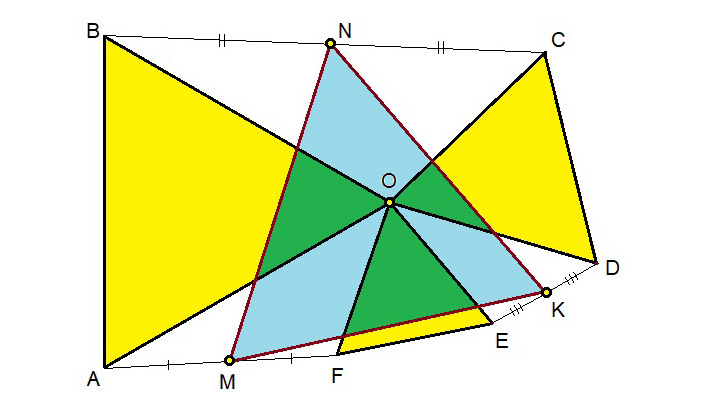
Рис. 7.

Эта красивая задача-изюминка «пришла» к нам с венгерской математической олимпиады школьников (ее можно найти в книге Венгерские математические олимпиады на с. 198). Из нее легко следует, что синий треугольник на рис. 6 равносторонний.

Можно пойти еще дальше. На одном из финалов Всероссийской математической олимпиады школьников член жюри и математик МФТИ Л. П. Купцов рассказал о еще одном обобщении этой задачи. Оказывается, если ко всем вершинам правильного треугольника O₁O₂O₃ шарнирно прикрепить вершинами равносторонние треугольники O₁AB, O₂CD и O₃EF (рис. 8), то треугольник, вершины которого совпадают с серединами отрезков FA, BC и DE — равносторонний.

Рис. 8.

Можно посмотреть на интерактивный чертеж этой задачи, который построил мой ученик Сергей Прика. На чертеже исходные треугольники можно перемещать («зажимая» их внутренность), а также можно изменять их размеры, перетягивая вершины B, D, F, O₁ и O₃ (они синего цвета). Посмотрев на это всё в динамике, можно убедиться, что как бы ни располагались крайние равносторонние треугольники, треугольник MNK всегда остается равносторонним (разумеется, это не доказательство — порешайте эту задачу самостоятельно). Удивительно красивые обобщения встречаются на бесконечных просторах планиметрии!

Оказывается, есть задачи, которые, хоть внешне и похожи на предложенные, не решаются только с помощью последнего обобщения. Пример — слева на рис. 9. Основные этапы решения также показаны на рис. 9.

Рис. 9.

Можно придумать и другие аналогичные конфигурации, для решения которых придется пользоваться последним обобщением.

Но все-таки, существует ли универсальный подход к решению подобных задач? Ответ положительный — он существует, причем очень наглядный и не требующий громоздких вычислений. Этот подход тоже основан на использовании треугольной сетки, но она в два раза мельче тех, что мы использовали до этого момента: сторона ее ячейки в четыре раза меньше стороны шестиугольника (рис. 10). При таком размере ячеек середины отрезков (то есть вершины синих треугольников) попадут точно в узлы сетки. Далее нужно заметить, что во всех случаях сторонами «синих» треугольников являются диагонали равных параллелограммов, составленных из нескольких треугольных ячеек сетки, поэтому все треугольники равносторонние.

Рис. 10.

Более того, в каждом отдельном случае легко найти зависимость стороны равностороннего треугольника от стороны правильного шестиугольника, рассчитав длину диагонали одного из трех видов параллелограммов (рис. 11).

Рис. 11.

Если сторону исходного шестиугольника принять равной 4a, то диагонали AC этих параллелограммов соответственно равны \(a\sqrt7\), \(a\sqrt{13}\) и \(a\sqrt{12}\), значит, стороны треугольников именно такие.

Вот так аккуратно нарисованный чертеж на фоне правильно подобранной сетки позволяет легко установить связь между элементами задачи, после чего ее решение становятся почти очевидным.