«Минус-кубики»

Попытайтесь замостить «минус-кубиками» бесконечный во все стороны плоский слой толщиной в два единичных кубика.

Попробуйте сформулировать и решить плоский аналог задачи на разрезание, а затем по аналогии найти разрезание «минус-кубика» на восемь равных частей.

а) Можно. В самом деле, из двух минус-кубиков можно сложить прямую призму, в основании которой лежит невыпуклый восьмиугольник, составленный из семи единичных квадратов (рис. 2, слева). Такими призмами, подобно тротуарной плитке, можно заполнить бесконечный плоский слой (рис. 2, справа), а затем такими слоями — и все пространство.

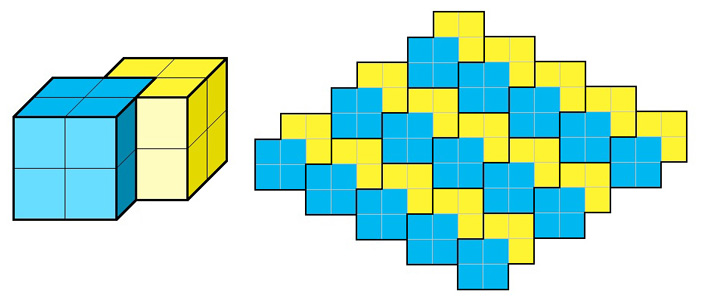
Рис. 2. Слева — из двух «минус-кубиков» можно составить призму. Справа — такими призмами можно замостить плоский слой (толщиной в два кубика), а такими слоями — все пространство

Прежде чем отвечать на второй вопрос этого пункта, разберемся с пунктом б).

б) Можно. Разобьем каждый кубик 1×1×1, из которых состоит «минус-кубик» на восемь «половинчатых» кубиков \(\frac12\times\frac12\times\frac12\). Теперь в каждом кубике 1×1×1 удалим тот «половинчатый» кубик, одна из вершин которого совпадает с центром исходного куба 2×2×2. В результате получится, что каждый из семи кубиков 1×1×1 тоже стал «минус-кубиком» (вдвое меньшего размера чем исходный, рис. 3, слева). Но семь удаленных кубиков \(\frac12\times\frac12\times\frac12\) месте составляют еще один «минус-кубик» 1×1×1. Если его добавить обратно, то получится разбиение исходного «минус-кубика» 2×2×2 на восемь вдвое меньших «минус-кубиков» (рис. 3, справа).

Рис. 3. Слева — исходный «минус-кубик» состоит из семи обычных кубиков 1×1×1, но если из каждого из них удалить по одному кубику \(\frac12\times\frac12\times\frac12\), то они превратятся в «минус-кубики» половинного размера. Удаленные маленькие кубики составляют восьмой «минус-кубик»

Теперь вернемся к вопросу о замощении «минус-кубиками» пространства, в котором уже есть один кубик 1×1×1. Понятно, что способом, описанным в решении пункта б), можно не только разбивать «минус-кубик» на вдвое меньшие, но и удваивать его — нужно просто сложить восемь копий так, как показано справа на рис. 3. Остается заметить, что в выемку можно добавить девятый «минус-кубик» и тот самый кубик 1×1×1, который изначально был, чтобы получить куб 4×4×4. Этот куб при помощи удвоенных «минус-кубиков» можно достроить до куба 8×8×8. Продолжая по аналогии, можно последовательно удваивать заполненную область пространства, и в результате замостить его полностью.

Очевидно, что пространство можно заполнить, например, кубами и параллелепипедами. Многогранниками более сложной формы это тоже можно делать. Оговоримся, что здесь речь идет об использовании копий одной фигуры. Куб, в частности, является единственным платоновым телом, копиями которого можно заполнить пространство (комбинируя другие платоновы тела, впрочем, заполнить пространство все-таки можно, см. задачу Платоновы тела и заполнения пространства).

Говоря о заполнении пространства копиями одной фигуры, обычно подразумевают, что ее можно отражать (то есть рассматриваются зеркальные копии этой фигуры). Однако есть класс многогранников, которые достаточно только параллельно переносить, чтобы заполнить всё пространство. Они называются параллелоэдрами. Кроме куба, который очевидно обладает таким свойством, параллелоэдрами являются еще четыре типа многогранников: шестиугольная призма, ромбододекаэдр, «двусторонне заточенный карандашик» и усеченный октаэдр.

Вообще, многогранник, копиями которого можно замостить все пространство, называется стереоэдром.

Вернемся к кубу 2×2×2, составленному из восьми единичных кубиков. Если из такого куба убирать единичные кубики по одному, то будут получаться многогранники, показанные на рис. 4.

Рис. 4.

Таким образом, удаляя из кубика 2×2×2 несколько кубиков 1×1×1, можно получить 12 различных многогранников, пронумерованных в таблице латинскими буквами от A до L.

Интересно, что каждый из полученных таким образом многогранников является стереоэдром.

1) Многогранники I, K и L — параллелепипедами, поэтому они стереоэдры.

2) Многогранники B, D, G, H и J тоже являются стереоэдрами, потому что из двух многогранников каждого вида можно сложить параллелепипед (рис. 5)

Рис. 5.

3) Из пункта а) следует, что многогранник A является стереоэдром. Тем же способом «тротуарной плитки», использованном в решении можно показать, что многогранники E и F тоже являются стереоэдрами. На рис. 6 показано, как из двух фигур каждого вида строится прямая призма, в основании которой лежит планигон — многоугольник, которым можно замостить плоскость. Значит, из таких призм можно сложить плоский слой толщиной в два кубика, а такими слоями — заполнить пространство.

Рис. 6.