Покадровая съемка

На примере третьего пункта можно заметить, что существуют большие наборы кадров, по которым, тем не менее, нельзя восстановить траекторию мяча. Например, если мяч оказывается на этих кадрах в равноотстоящих друг от друга по горизонтали точках на одинаковой высоте, то можно пустить через них любую траекторию с периодом, делящим расстояние между соседними точками. Однако такие вырожденные конфигурации редки, и естественно их не учитывать. Подумайте, в каком именно смысле они «редки», — мы обсудим этот вопрос в решении.

Если не учитывать вырожденные случаи, минимальное достаточное число кадров в первом пункте — 4. Попробуйте построить для этого пункта вырожденный набор из 4 точек с неоднозначным ответом.

1) В отсутствие сопротивления воздуха мяч между отскоками от поверхности будет двигаться по параболе (ветви которой смотрят вниз). Поскольку отскок упругий, то вся его траектория представляет собой набор из таких одинаковых парабол (получаемых сдвигом одна из другой), которые пересекаются в точках отскока от поверхности (рис. 1). По сути, задача сводится к следующей: определить, по скольким известным точкам однозначно восстанавливается траектория такого типа. Промежутки между соседними точками отражения от поверхности далее будем называть периодом траектории.

Рис. 1.

Из Основной теоремы алгебры следует, что через любые n + 1 точек «проходит» единственный многочлен степени n (две основных конструкции такого многочлена — Ньютона и Лагранжа). Так как парабола задается многочленом второй степени, то если на одной из парабол (участке траектории между отскоками) будет известно три точки, траектория восстановится однозначно. Можно показать, что любая параболическая траектория физически возможна, коль скоро ее ветви направлены вниз и вершина выше горизонтальной оси (то есть выше поверхности, от которой отскакивает мяч).

Допустим, имеется три кадра. То есть известны три точки — А, В и С (слева направо) — на траектории мяча (считаем, что они не лежат на одной прямой — этот случай несложно разобрать отдельно). Проблема в том, что в общем случае неизвестно место отскока, поэтому нельзя сразу сказать, попадают ли эти точки в один период. Можно предположить, что это так, и получить вариант траектории — параболу, проходящую через эти три точки.

А можно предположить, что где-то между точками был отскок. Тогда две из них — пусть это А и В — попадают на один период, а третья — на соседний. Мы не знаем, где был отскок, — знаем только, что где-то между В и С. Но нам этого достаточно. Рассуждение следующее. Выберем точку Х на горизонтальной оси между В и С и будем считать, что она и есть точка отскока. Тогда по точкам А, В и Х восстанавливается гипотетическая траектория. Если точка С попала на нее, то мы получили вторую траекторию для данной тройки точек. Но что если точка С на нее не попадает? Ничего страшного: мы можем двигать точку Х. Заметим, что если Х придвигать к точке В, то параболу можно сделать сколь угодно «крутой». Если двигать точку Х вправо от В к С, то парабола начнет «толстеть», а соседний период будет также сдвигаться вправо (рис. 2). Таким образом можно замести некоторую область на плоскости (какой кривой она ограничена?), и если точка С попала в эту область, то мы опять получаем второй вариант траектории мяча (поскольку она, очевидно, будет отличаться от траектории, в которой все три точки попали на один период).

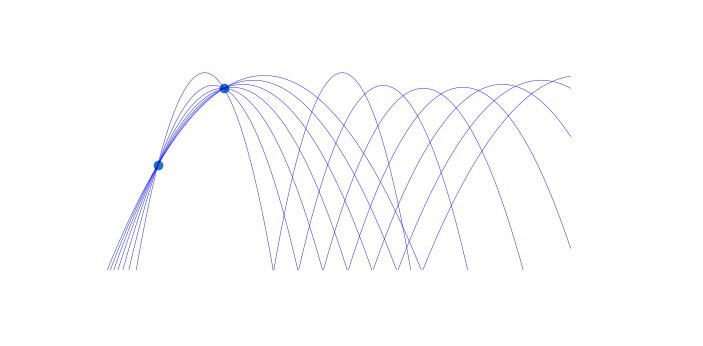
Рис. 2.

На самом деле, если точка С лежит «достаточно низко», то таким способом можно получить даже две траектории: в одном случае эта точка попадет на восходящую ветвь параболы, а в другом — на нисходящую (рис. 3).

Рис. 3.

Важно, что в пределах описанной области (которая определяется положением точек А и В) третью точку можно выбирать произвольно — и дополнительная траектория всегда будет. Приведенное выше рассуждение не совсем формально, но при желании его можно свести к решению системы уравнений.

Итак, в общем случае трех точек явно не хватает.

Допустим теперь, что известны четыре точки траектории. Хотя в нем тоже существуют конфигурации с неоднозначным ответом (рис. 4), но качественное отличие этого случая от предыдущего в том, что здесь, неформально говоря, нельзя произвольно подвинуть одну из точек так, чтобы неоднозначность сохранилась. Это можно обосновать аналогично предыдущим рассуждениям: если на один период попали три или все четыре точки, то траектория заведомо однозначна, а если на два периода попало по две точки, то, двигая точку отскока, нужно подогнать параболу уже не под одну, а под две точки, что дает ограничение на взаимное положение точек.

Рис. 4.

С интуитивно-вероятностной точки зрения это означает, что при случайном выборе точек наблюдения такая ситуация вряд ли возникнет. Напротив, для трех точек хватало, чтобы третья точка попадала в достаточно большую область, задаваемую первыми двумя, — вполне вероятное событие. Говоря формально, множество точек неоднозначности решения имело ненулевой объем в конфигурационном пространстве.

Рисунок 4, конечно, показывает, что для ответа на поставленный в первом пункте вопрос вышеизложенные рассуждения не очень нужны. Но они позволяют понять, что вообще происходит в рассматриваемой ситуации, и практически аналогичны рассуждениям, которые нужны в пункте 3.

В случае же пяти точек ответ всегда однозначен без каких-либо оговорок — это следует из того, что две различных траектории (с не более чем одним отскоком каждая) могут иметь не более четырех точек пересечения, что проверяется геометрически или путем составления уравнения.

2) Теперь рассмотрим случай, когда известен момент прохождения каждой точки. Это сильно упрощает анализ. Если известны две точки на одном интервале, то парабола восстанавливается однозначно: можно составить линейную систему из двух уравнений на компоненты вектора начальной скорости. Осталось заметить, что, при условии наличия отскока, двух точек, очевидно, не хватит, а если есть три точки траектории, то хотя бы две из них попадают на один интервал (но, хотя иногда и возможны два разных решения, целой области неоднозначности не будет потому, что два участка траектории связаны условием на совпадение вертикальной скорости).

3) Как сказано в первой подсказке, если принимать во внимание вырожденные случаи, то никакого числа точек не хватит для однозначного ответа (рис. 5). Поэтому будем разбираться с ситуацией, когда точки в достаточно общем положении.

Рис. 5.

Для начала рассмотрим вариант, когда известны моменты времени, в которые произведены измерения. Рассмотрим две самые левые точки. Если зафиксировать число отскоков между ними, то траектория восстанавливается однозначно (из физических соображений). Таким образом, перебирая число отскоков, можно найти такую траекторию, на которую лягут оставшиеся точки. Из дискретности этого параметра следует, что достаточно еще одной точки общего положения (у траекторий при различном числе отскоков есть пересечения, но они изолированы и областей неоднозначности нет). То есть в этом варианте достаточно трех точек.

Покажем, как свести вариант с неизвестными метками времени к только что рассмотренному. Для этого достаточно ввести непрерывный параметр — горизонтальную компоненту скорости (она ведь постоянна, поскольку отскоки упругие). Тогда время измерений восстанавливается с точностью до начала отсчета. Чем больше скорость, тем более «плоской» будет траектория при прочих равных условиях. Добавив еще одну точку в произвольном месте, мы можем восстановить подходящее значение этого параметра.

4) Этот пункт был добавлен в задачу достаточно спонтанно, и, как оказалось, первоначальные соображения автора относительно решения не подтвердились. Так что на данный момент вопрос остается открытым — делитесь идеями в комментариях!

В данной задаче мы рассмотрели восстановление непрерывной траектории по отдельным точкам. Подобного рода задачи называются задачами интерполяции, и ими занимается отдельный раздел вычислительной математики. В решении зашла речь о том, что измерять положения мячика нужно в случайные моменты времени, — тогда нас минует опасность нарваться на неоднозначность. Посмотрим, какие еще естественные требования стоит наложить, если вдруг требуется установить траекторию как можно точнее.

Понятно, что любое измерение производится с какой-то погрешностью. В нашей модели с мячиком это означает, что положения мяча на фотографиях могут немного отличаться от реальных (из-за дрожания камеры, например). Что происходит с восстановленной траекторией, если немного передвинуть точки? Можно заметить, что если измеренные точки находятся близко друг от друга, то даже слабое перемещение одной из них значительно меняет траекторию, а в случае с далеко отстоящими друг от друга точками такого не происходит. Это означает, что следует разнести измерения во времени, чтобы уменьшить возможную ошибку. С математической точки зрения говорят о том, как задача обусловлена. Хорошо обусловленная задача поставлена так, что небольшое изменение входных данных влечет за собой только небольшое изменение ответа. На практике это означает, что небольшая ошибка при измерениях не сильно испортит результат. Для оценки того, насколько сильно портится результат, вводится число обусловленности, которое, грубо говоря, задает верхнюю границу изменения ответа при фиксированном приращении входных данных.

Стоит отметить, что кроме погрешности измерений есть и другие источники ошибок. Например, числа на компьютере хранятся с конечной точностью, и поэтому при вычислениях неизбежно накапливается погрешность из-за округления. При этом вычисления, которые на бумаге эквивалентны, могут давать разную ошибку в зависимости от порядка действий.

История знает немало примеров того, как такого рода ошибки приводили к катастрофическим последствиям. Например, в системе управления американской зенитной ракетной установкой Patriot требовалось делить время, прошедшее с момента включения бортового компьютера, на 10. Проблема в том, что 0,1 — хорошая дробь в десятичной системе, а вот в двоичной ее запись бесконечна (и выглядит вот так: 0,000110011001100..., поскольку 1/10 = 1/2⁴ + 1/2⁵ + 1/2⁸ + 1/2⁹ + 1/2¹² + 1/2¹³ + ...). Поэтому константа 0,1 хранилась неточно. Ошибка была маленькая, но однажды при умножении на большое число, когда запуск ракеты был произведен спустя долгое (несколько суток) время после запуска управляющей системы, ошибка привела к промаху в несколько сотен метров. Отсюда появляется потребность оценивать обусловленность не только задачи, но и используемого численного метода. Часто на практике приходится применять чрезмерно сложные с теоретической точки зрения методы только потому, что у них хорошая обусловленность

Автор благодарит за помощь и ценные замечания Евгения Епифанова и Никиту Волкова.