Потяни за веревочку

Подумайте о физической причине того, что веревку приходится тянуть с силой, превышающей вес тела. Какие дополнительные силы могут быть тут замешаны?

Два с половиной оборота веревки вокруг шеста — это пять раз по пол-оборота. Разделите мысленно намотанную часть веревки на пять участков по пол-оборота и рассмотрите каждый такой «кусок» веревки отдельно. Пусть за один конец куска тянут с силой F. С какой силой надо потянуть за другой конец, чтобы привести его в движение?

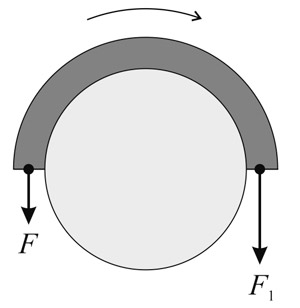
Рис. 2

Рассмотрим участок веревки, занимающий пол-оборота вокруг шеста, как показано на рис. 2. Пусть слева веревку тянут с силой F. Попробуем сначала ответить на такой вопрос: с какой силой F₁ надо тянуть веревку справа, чтобы привести ее в движение по часовой стрелке? Сразу оговоримся, что, так как веревка легкая, сила тяжести, действующая на нее, пренебрежимо мала и положение рассматриваемого куска не играет роли. То есть наши выводы не будут зависеть от того, верхнюю или нижнюю половину шеста занимает рассматриваемый нами кусок.

Из условий задачи мы знаем, что при силе F, равной весу груза, сила F₁ = 1,3F. Единственной причиной, по которой F₁ превышает F, может быть наличие трения. По закону Амонтона — Кулона сила трения скольжения между веревкой и поверхностью шеста пропорциональна силе нормальной реакции между ними. Представим, что мы увеличили силу F в некоторое количество раз. Тогда в то же количество раз возрастет сила реакции и, соответственно, сила трения. Следовательно, в то же число раз возрастет сила F₁. Отсюда можно сделать вывод, что сила F₁ зависит от F линейно, и выражение F₁ = 1,3F справедливо для любой величины F.

Теперь рассмотрим ситуацию, когда веревка обернута вокруг шеста два с половиной раза, как в условии задачи. Мысленно разделим эти два с половиной оборота веревки на пять частей по пол-оборота каждая. Тогда первую часть веревки тянет вниз груз с силой, равной своему весу P. Чтобы привести этот участок веревки в движение, второй участок веревки должен тянуть его c силой 1,3P. При этом первый участок веревки по третьему закону Ньютона действует на второй с той же силой 1,3P. Поэтому, чтобы привести в движение второй участок, третий должен тянуть его с силой 1,3·1,3P = 1,69P. Продолжая аналогичные рассуждения, делаем вывод, что для приведения в движение всей веревки за ее свободный конец надо потянуть с силой (1,3)⁵P = 3,71P, то есть в 3,71 раза превышающей вес груза.

Результат решения задачи выглядит несколько неожиданно. Получается, что с ростом числа оборотов веревки сила, с которой ее надо тянуть, растет в геометрической прогрессии! Однако, если задуматься, такой вывод хорошо согласуется с нашим повседневным опытом. Вспомним, как мы зачастую привязываем веревку к чему-нибудь круглому: наматываем несколько оборотов, а затем фиксируем свободный конец самым простым узлом, а то и просто затыкаем его за намотанную часть. И несмотря на то, что удерживает этот конец совсем незначительная сила, другой конец веревки проще оборвать, чем вытянуть.

Рис. 3

Для того чтобы понять физическую причину этого эффекта, нужно рассмотреть систему на более глубоком уровне, а точнее, мысленно разрезать веревку на еще меньшие кусочки. Рассмотрим совсем маленький кусочек веревки, угловой размер Δα которого очень мал, как показано на рис. 3. Пусть слева наш кусочек тянут с силой F. Определим, с  какой силой F₁ его надо тянуть справа, чтобы привести в движение. Для этого сначала определим все силы, действующие на кусочек. Кроме F и F₁ это сила нормальной реакции опоры (шеста) N и сила трения скольжения T. По закону Амонтона — Кулона T = kN, где k — коэффициент трения. Запишем второй закон Ньютона для кусочка в проекции на касательную ось x. Получаем F₁ = F + kN, так как ускорение равно нулю (тут косинусы малых углов между направлениями сил и осью x заменены единицей). В проекции на радиальную ось y получаем N = FΔα/2 + F₁Δα/2 (тут синусы малых углов заменены величинами этих углов). Отсюда для разности ΔF = F₁ – F получаем ΔF = k(F + ΔF/2)Δα. Так как ΔF получается малой величиной (порядка Δα), то по сравнению с F ей можно пренебречь, и окончательно получаем ΔF = kFΔα.

Теперь становится ясна причина быстрого возрастания силы натяжения нити. Если бы коэффициент между ΔF и Δα был постоянным, сила натяжения возрастала бы с углом линейно. Соответственно, добавление каждого оборота веревки увеличивало силу натяжения на фиксированную величину. В нашем же случае коэффициент между приращением угла и приращением силы натяжения сам зависит от силы натяжения. Таким образом, чем больше сила натяжения, тем быстрее она растет. С использованием техники дифференциальных уравнений можно показать, что этот рост будет экспоненциальным. Для тех, кто с этой техникой знаком, предлагается дополнительное задание: по данным задачи определить коэффициент трения между веревкой и шестом.