Мозаики и замощения
-
30.07.2025Апериодическая плиткаХайдар Нурлигареев • Библиотека • «Квантик» №11, 2024
-
28.04.2023Замощение Соколара — ТейлорМихаил Грунтов, Хайдар Нурлигареев • Картинки дня
-
28.04.2023Решена «задача Эйнштейна» о замощении плоскости
«Задача Эйнштейна» — это шутливое название важного вопроса из теории замощений, который заключается в следующем: существует ли такой многоугольник, что его копиями можно замостить всю плоскость, причем любое получающееся замощение окажется непериодическим? В марте в архиве электронных препринтов появилась статья, в которой дается положительный ответ: апериодическая моноплитка существует.
Хайдар Нурлигареев • Новости науки
-
29.08.2021Теорема Наполеона, замощения плоскости и параллельникиГригорий Мерзон • Библиотека • «Квантик» №12, 2020
-
21.07.2021Замощения параллелоэдрамиАлексей Гарбер • Библиотека • «Квант» №1, 2019
-
03.06.2021Мозаика РобинсонаХайдар Нурлигареев • Библиотека • «Квантик» №10, 2020
-
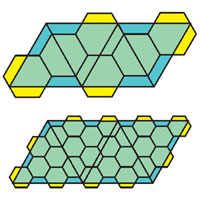30.05.2021Оклейка тетраэдра шестиугольникамиНиколай Авилов • Библиотека • «Квант» №10, 2018
-
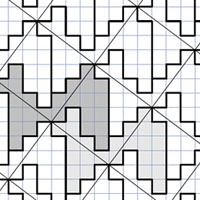06.12.2020Как разрезать верблюда?Григорий Мерзон • Библиотека • «Квантик» №5, 2020
-
03.06.2020Плитки и числа ХеешаХайдар Нурлигареев • Библиотека • «Квантик» №10, 2019
-
09.08.2019Ковер Серпинского
Ковер Серпинского — это типичный пример фрактальной фигуры. Как и для абсолютного большинства фракталов, ему присуще свойство самоподобия, а также другие интересные свойства.Хайдар Нурлигареев • Картинки дня
-
18.10.2018Самоподобные замощенияХайдар Нурлигареев • Картинки дня
-
14.09.2018Мозаика Робинсона
На картинке изображен фрагмент мозаики Робинсона, представляющей собой пример апериодического замощения плоскости многоугольниками. Любой конечный фрагмент мозаики Робинсона встречается в ней бесконечно много раз. А между тем, до середины XX века считали, что апериодических протомножеств не существует вовсе.Хайдар Нурлигареев • Картинки дня
-
16.04.2018«Жесткие» замощения
а) Найдите углы и соотношения сторон треугольников замощения, показанного на рисунке. Докажите, что из рисунка они определяются однозначно. б) Придумайте «жесткое» замощение из равных выпуклых четырехугольников. в) Придумайте «жесткое» замощение из равных пятиугольников (не обязательно выпуклых).
Хайдар Нурлигареев • Задачи
-
14.08.2017Полоски из домино
а) Сколькими способами можно замостить полосу 2×10 доминошками 2×1? Замощения, получающиеся друг из друга вращением полосы, считаются разными. б) Тот же вопрос для полосы 3×30.
Хайдар Нурлигареев • Задачи
-
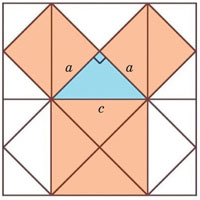10.03.2017Сокровище геометрииНаталья Карпушина • Библиотека • «Наука и жизнь» №9, 2016
-
20.04.2015Паркеты из полимино
а) Придумайте три различных замощения плоскости данными фигурками пентамино. б) Докажите, что существует бесконечно много различных замощений плоскости данными фигурками нонамино. в) Приведите пример еще одной фигурки гептамино, копиями которой нельзя замостить плоскость без пробелов и наложений.
Хайдар Нурлигареев • Задачи
-
20.03.2011Замощения
Докажите, что любым треугольником и любым четырехугольником можно замостить плоскость. Приведите пример пятиугольника, которым можно замостить плоскость. Приведите пример шестиугольника, которым нельзя замостить плоскость. Приведите пример n-угольника для какого-либо n > 6, которым можно замостить плоскость.
Хайдар Нурлигареев • Задачи
Последние новости
Картинка дня
