Оклейка тетраэдра шестиугольниками

Николай Авилов
«Квант» №10, 2018

В этой статье пойдет речь о конкурсной задаче № 4998 из журнала «Математика в школе»:

Можно ли поверхность правильного тетраэдра оклеить (без пропусков и перекрытий) одинаковыми правильными шестиугольниками?

Скажем сразу, что ответ на вопрос задачи положительный. На рисунке 1 показано шесть решений задачи из их бесконечного множества.

Рис. 1

В каждом из решений основой развертки тетраэдра является параллелограмм, состоящий из четырех правильных треугольников. На этот параллелограмм наложен многоугольник, содержащий несколько правильных шестиугольников. Если многоугольник, составленный из правильных шестиугольников, перегнуть по сторонам всех треугольников, то при складывании тетраэдра из треугольной развертки будет складываться тетраэдр из шестиугольников, при этом шестиугольники покроют поверхность тетраэдра полностью, без пропусков и перекрытий.

Уточним, что в первой серии решений (см. рис. 1; левый столбец) вне параллелограмма находится несколько трапеций, и ровно столько же таких трапеций не накрыли параллелограмм, причем при складывании тетраэдра «выступающие» трапеции как раз займут место «недостающих» трапеций в развертке.

Во второй серии решений (см. рис. 1; правый столбец) ситуация похожая, разница лишь в том, что здесь роль трапеций выполняют треугольники.

Можно было бы поставить точку — ведь задача решена, приведены конкретные развертки. Но попробуем заглянуть чуть дальше, например, ответить на вопрос: «Как отыскать эти решения?»

Пусть ребро тетраэдра равно a, сторона правильного шестиугольника равна b, тогда площадь поверхности тетраэдра равна \( a^2\sqrt{3} \), а площадь шестиугольника равна \( \frac{3}{2} b^2\sqrt{3} \).

Пусть для оклейки понадобится \( n \) ( \( n \in \mathbb{N} \)) шестиугольников, тогда если тетраэдр оклеивать шестиугольниками без пропусков и перекрытий, то получим уравнение \( n · \frac{3}{2} b^2\sqrt{3} = a^2\sqrt{3} \), откуда \( n = \frac{2}{3}\left(\frac{a}{b}\right)^2\).

Заметим, что если \( \frac{a}{b} = 3k \) , \( k \in \mathbb{N} \), то \( n \) станет натуральным числом вида \( 6k^2 \). При каждом натуральном значении \( k \) получим одно из решений первой серии. Это значит, что тетраэдр можно оклеить 6, 24, 54, 96, ..., 6k² правильными шестиугольниками. Такое решение, содержащее шесть шестиугольников, было первым решением обсуждаемой задачи.

Следующей находкой было решение, которое обнаружили А. М. Домашенко из Новошахтинска и К. Д. Ашурбеков из Махачкалы. Они нашли удивительное решение, содержащее всего лишь два шестиугольника, и заметили, что если \( \frac{a}{b} = k \sqrt{3} \), то n станет натуральным числом вида 2k². Именно к этому случаю относится их решение при k = 1. Таким образом, была найдена вторая серия решений задачи. При каждом натуральном значении k получим одно из решений этой серии. Это значит, что тетраэдр можно оклеить также таким количеством правильных шестиугольников: 2, 8, 18, 32, ..., 2k².

Интересно отметить, что в каждой серии решений длины сторон шестиугольников образуют гармонический ряд, т.е. если в первом решении длину стороны принять за единицу, то последовательность длин сторон будет такой: \( 1, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, ..., \frac{1}{n}, ... \)

Вполне возможно, что оклеить тетраэдр можно и другим количеством правильных шестиугольников, потому что существует много других значений дроби \( \frac{a}{b} \), когда n будет натуральным числом. Например, \( \frac{a}{b} = k\sqrt{6} \). Но вопрос здесь остается открытым.

Несмотря на это, находки продолжаются. Существует весьма интересная интерпретация первого решения обсуждаемой задачи. Ее можно считать оригинальной головоломкой-трансформером. Представляет она собой бумажное кольцо, содержащее шесть правильных шестиугольников, последовательно соединенных друг с другом противоположными сторонами длиной b (рис. 2). Его нетрудно вырезать и склеить из бумаги, лучше — из ватмана.

Рис. 2 и 3

Оказывается, такое кольцо путем нескольких перегибаний можно трансформировать в правильный тетраэдр. Важно при этом на поверхности кольца правильно определить отрезки перегибаний. Учитывая, что площадь кольца и площадь поверхности тетраэдра равны, легко установить, что ребро тетраэдра равно 3b. Теперь на поверхности кольца нужно отыскать эти отрезки и перегнуть по ним.

Проделайте это самостоятельно, уверяю, получите при этом ничем не заменимое удовольствие. Если же тетраэдр не сложится, то следуйте инструкции.

На первом шаге сделаем четыре перегиба длиной 1,5b поперек кольца, делящих его на четыре части одинаковой длины (рис. 3). Каждый перегиб проходит через середины сторон шестиугольника. Взглянув после этого на кольцо сверху, можно заметить контур квадрата.

Рис. 4 и 5

Следующим шагом нужно сделать еще четыре косых перегиба длиной 3b, которые вместе образуют замкнутую ломаную — пространственный четырехугольник со стороной 3b (рис. 4).

Если теперь взяться пальцами за вершины этого четырехугольника и две противоположные вершины поднимать вверх, а две другие опускать вниз, то вся конструкция, как ни удивительно, превратится в бумажную модель правильного тетраэдра (рис. 5).

Вот такие чудеса встречаются в геометрии.

Можно пойти еще дальше в этом направлении. Оказывается, тетраэдр можно сложить также из двух колец, каждое из которых содержит по 12 шестиугольников; из трех колец по 18 шестиугольников. В этом можно убедиться, наверное, только путем моделирования. Я это проделал и не пожалел, потому что появилась возможность обобщения: тетраэдр можно сложить из k колец, каждое из которых содержит по 6k шестиугольников.

Рис. 6

На рисунке 6 приведена иллюстрация этого обобщения при k = 3. Слева изображены три бумажных кольца, каждое из которых содержит 18 шестиугольников. Справа — модель правильного тетраэдра, обернутая этими кольцами.

Были попытки объединить все шестиугольники в одно кольцо и сложить тетраэдр из одного длинного кольца, в котором 6k² шестиугольников, но они оказались безуспешными.

Новую находку пришлось ждать недолго. А. М. Домашенко заметил, что «шестилепестковая ромашка», содержащая семь равных правильных шестиугольников, равновелика правильному шестиугольнику. Это легко увидеть на рисунке 7.

Рис. 7

Это позволило ему трансформировать ранее найденное им решение, содержащее два шестиугольника, заменив каждый шестиугольник «ромашкой» так, что получилась «развертка» тетраэдра, в котором уже 14 шестиугольников. Такую же замену можно проделать с каждой «разверткой» второй серии. Это значит, что найдена третья серия решений, и тетраэдр можно оклеить 14, 56, 126, 224, ..., 14k² правильными шестиугольниками.

Если такую трансформацию проделать с первой «разверткой» первой серии, то получим решение задачи, содержащее 42 шестиугольника, а вместе с ним новую, уже четвертую, серию решений, в которой 42, 168, 378, 672, ..., 42k² правильных шестиугольника.

Многие свойства первой и второй серии решений, описанные выше, остаются верными и в третьей, и в четвертой. Например, в каждой новой серии решений длины сторон шестиугольников образуют гармонический ряд. Первые «развертки» тетраэдров в каждой серии можно представить в виде одного замкнутого кольца; вторые «развертки» тетраэдров в каждой серии можно представить в виде объединения двух замкнутых колец; третьи «развертки» — это объединение трех замкнутых колец и так далее.

Рис. 8

На рисунке 8 показано замкнутое кольцо из 14 правильных шестиугольников и тетраэдр, сложенный из этого кольца.

На рисунке 9 приведена «развертка» тетраэдра, содержащая 56 правильных шестиугольников. Здесь же показана схема, как этот тетраэдр сложить из двух замкнутых колец — синего и желтого, в каждом из которых по 28 правильных шестиугольников, пронумерованных числами от 1 до 28. Стрелками указано направление перехода от одного шестиугольника к соседнему по кольцу.

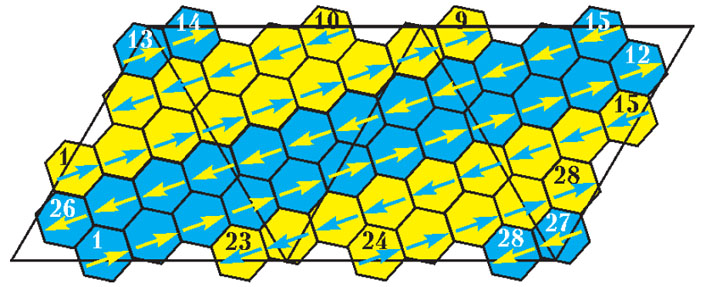
Рис. 9

Но самое интересное, что отношение сторон \( \frac{a}{b} \) в этих случаях равно \( k\sqrt{21} \) и \( 3k\sqrt{7} \) соответственно. Кто бы мог предположить, что отношение сторон может быть именно таким! Теперь класс чисел, которые могут выступать в качестве отношения сторон, значительно расширился, а значит, шанс найти новые серии решения увеличился.

Находку А. М. Домашенко можно развить, если заметить, что «ромашка», содержащая 19 равных правильных шестиугольников, также равновелика правильному шестиугольнику. На рисунке 10 слева это легко увидеть, а на рисунке 10 справа показано, как из двух таких «ромашек» можно сложить развертку тетраэдра.

Рис. 10

Если продолжить обобщение в этом направлении, то получим новую серию решений (рис. 11): 2, 14, 38, 74, ... , 2(3k² − 3k + 1) на основе последовательности чисел 1, 7, 19, 37, ..., 3k² − 3k + 1 (которые Мартин Гарднер называет гексами).

Рис. 11

Вот пока все находки в окрестности этой задачи, которые удалось отыскать на данный момент. Всем, кого заинтересовала эта задача, или тем, кто отыщет новую находку, предлагаю обращаться по адресу avilow@rambler.ru.