Теорема Наполеона, замощения плоскости и параллельники

Григорий Мерзон
«Квантик» №12, 2020

1. В одном из первых номеров журнала «Квантик» рассказывалось¹ про две замечательные теоремы.

Теорема Наполеона. Центры равносторонних треугольников, построенных вовне на сторонах произвольного треугольника, образуют равносторонний треугольник.

Теорема Тебо. Центры квадратов, построенных вовне на сторонах произвольного параллелограмма, образуют квадрат.

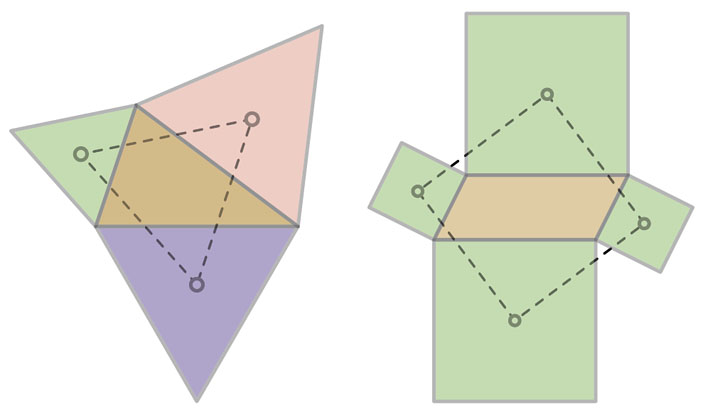
Оказывается, с этими теоремами связаны два замечательных замощения плоскости.

Изображения, расположенные на с. 20

Если долго смотреть на эти замощения, то и теоремы станут очень понятными!²

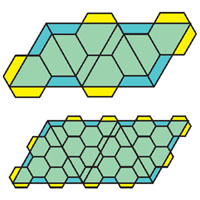
Посмотрим, например, на правую картинку внизу с. 20. Центры больших квадратов образуют квадратную сетку — то есть можно считать, что картинка нарисована на клетчатой бумаге и центры больших квадратов лежат в её узлах. А центры маленьких квадратов тогда лежат в центрах клеточек. Поэтому теорема Тебо верна.

Впрочем, если такое рассуждение вы расскажете своему учителю геометрии, то у него наверняка возникнут вопросы, о которых действительно полезно подумать. Ну а пока продолжим смотреть на картинки.

Точно так же на левой картинке внизу с. 20 можно увидеть теорему Наполеона³. Только треугольники теперь лежат в вершинах не квадратной, а треугольной сетки.

2. Не правда ли, формулировки двух теорем довольно похожи и вызывают надежду, что это начало целой серии теорем?

Но если в теореме Наполеона речь идёт о произвольном треугольнике, то в теореме Тебо уже нельзя брать произвольные четырёхугольники (в этом легко убедиться, нарисовав, например, очень сплюснутую трапецию), годятся только параллелограммы.

А что нужно потребовать, скажем, от пятиугольника, чтобы для него выполнялась теорема, аналогичная теореме Наполеона?

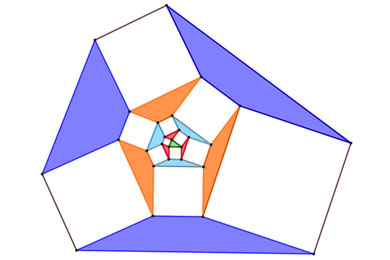
Тут помогает понятие параллельника, недавно обсуждавшееся в «Квантике»⁴. Параллельник (или, выражаясь более научно, аффинно-правильный многоугольник) — это многоугольник, в котором параллельны друг другу те же стороны и диагонали, как если бы он был правильным. Например, четырёхугольный параллельник — это параллелограмм, а пятиугольный параллельник — такой пятиугольник, в котором каждая диагональ параллельна соответствующей (противоположной) стороне.

Теперь можно сказать, что обе приведённые теоремы — частные случаи такого утверждения.

Обобщённая теорема Наполеона. Центры правильных N-угольников, построенных вовне на сторонах произвольного N-угольного параллельника, образуют правильный N-угольник.

Но у этой теоремы нет наглядного доказательства при помощи замощений. Зато есть замечательно короткое доказательство при помощи комплексных чисел — но это уже совсем другая история.

Художник Мария Усеинова

¹ А. Полянский, Г. Фельдман. Наполеон и геометрия («Квантик» № 5 за 2012 год).

² Про другие доказательства при помощи замощений см. ещё статью: Г. Мерзон. Как разрезать верблюда? («Квантик» № 5 за 2020 год).

³ Подробнее про это написано в статье: В. Н. Дубровский. Геометрия на паркете («Квант» № 2 за 2014 год). Там же рассказывается и про другие доказательства при помощи замощений.

⁴ Ф. Нилов. Параллельники, полупараллельники и равные площади («Квантик» № 11 за 2020 год). Там на сторонах N-угольных параллельников строят не правильные N-угольники, а квадраты — и тоже получается интересно.