Решена «задача Эйнштейна» о замощении плоскости

Рис. 1. Фрагмент апериодического замощения плоскости копиями одной плитки. Рисунок с сайта cs.uwaterloo.ca

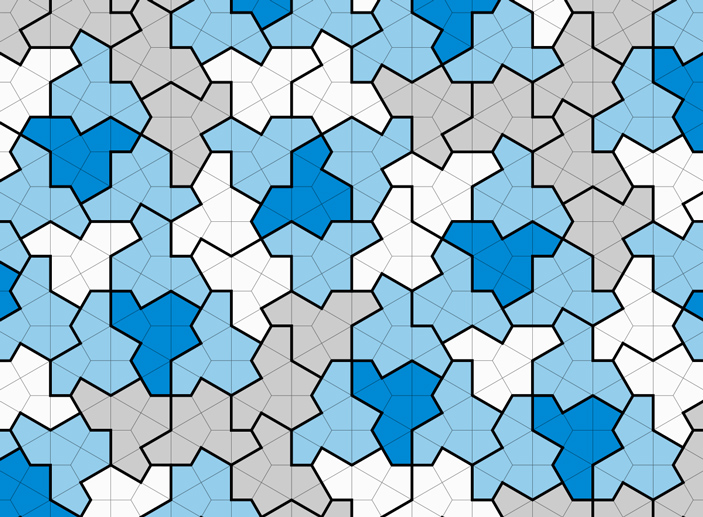
«Задача Эйнштейна» — это шутливое название важного вопроса из теории замощений, который мучил математиков не один десяток лет. Вопрос заключается в следующем: существует ли такой многоугольник, что его копиями можно замостить всю плоскость, причем любое получающееся замощение окажется непериодическим? Многоугольник с таким свойством называют апериодической моноплиткой. В марте в архиве электронных препринтов arxiv.org появилась статья, в которой дается положительный ответ: апериодическая моноплитка существует. Причем устроена она относительно просто — математики, потратившие на поиски решения десятилетия, ожидали увидеть в результате гораздо более заковыристую фигуру.

Замощением называется разбиение плоскости на многоугольники без пробелов и наложений. Иными словами, любая точка плоскости покрыта каким-то многоугольником, а сами многоугольники могут пересекаться только по границе. Вообще говоря, можно рассматривать замощения и более общими классами геометрических фигур, но мы сосредоточимся именно на многоугольниках. Замощения изучаются в математике уже довольно давно и для них было найдено немало важных приложений (в том числе, например, в кристаллографии и физике). Традиционно многоугольники замощения называют плитками (к тому же так короче). Фигуру, копиями которой можно замостить всю плоскость, называют моноплиткой. Придумать моноплитку несложно — подойдет треугольник или четырехугольник. На рис. 2 показаны два конкретных примера, но, действуя аналогично, можно замостить всю плоскость любым треугольником или четырехугольником.

Рис. 2. Периодические замощения плоскости треугольниками и четырехугольниками. Рисунок © Хайдар Нурлигареев

Приведенные на рис. 2 замощения периодические: они самосовмещаются при параллельном переносе на некоторый вектор (свой для каждого из этих двух замощений). Иногда по-другому не бывает. Скажем, плиткой в форме правильного шестиугольника замостить плоскость можно единственным образом, и это замощение является периодическим (рис. 3).

Рис. 3. Замощение плоскости шестиугольниками. Рисунок © Хайдар Нурлигареев

Некоторые моноплитки допускают также непериодические замощения. Так, если в периодическом замощении прямоугольными треугольниками, изображенном слева на рис. 4, перевернуть два примыкающих друг к другу по гипотенузе треугольника, то получится замощение, которое не совмещается с собой ни при каком параллельном переносе (рис. 4, справа) по очевидной причине: неоднородность в виде «неправильно» расположенных треугольников встречается лишь однажды.

Рис. 4. Как сделать из периодического замощения непериодическое. Рисунок © Хайдар Нурлигареев

А может ли быть так, что копиями некоторой моноплитки можно замостить всю плоскость — возможно, разными способами, но при этом любое такое замощение окажется непериодическим? Или, более общо, бывает ли так, что копиями плиток из некоторого конечного набора можно замостить плоскость только непериодически? Для таких наборов плиток существует специальное название — апериодические наборы, а соответствующие замощения плоскости называются апериодическими замощениями.

В начале 60-х годов XX века Хао Ван (Hao Wang) высказал предположение, что апериодических наборов плиток не существует. Иными словами, согласно гипотезе Вана, если некоторый конечный набор плиток допускает замощение плоскости, то есть если копиями плиток из этого набора можно замостить плоскость без пробелов и наложений, то обязательно найдется способ переупорядочить плитки так, чтобы полученное замощение оказалось периодическим. Однако уже в 1966 году Роберт Бергер (Robert Berger) показал, что гипотеза Вана неверна. В первоначальном доказательстве фигурировала конструкция, в которой использовалось аж 20426 различных плиток. Немного позже Бергеру удалось уменьшить это число до вполне обозримых 104 плиток. Так возник следующий вопрос: а каковым является минимально возможное число различных плиток в апериодическом наборе? И в частности, можно ли обойтись всего одной плиткой? Последний вопрос Людвиг Данцер (Ludwig Danzer) в шутку окрестил einstein problem, что на русский можно было бы перевести как «задача Эйнштейна». Однако прямой связи с одним из самых известных физиков XX века тут нет. Дело в том, что на немецком словосочетание ein stein дословно означает «один камень», что и отсылает нас к вопросу существования апериодической моноплитки.

Добиться первых промежуточных результатов на пути к одной моноплитке удалось довольно быстро. Сначала, в 1971 году, Рафаэль Робинсон придумал апериодический набор из 6 плиток (см. Мозаика Робинсона), а затем, в 1974 году, Роджер Пенроуз сократил минимальное число плиток в наборе до 2 (см. Мозаика Пенроуза). Однако наиболее амбициозная задача не поддавалась математикам гораздо дольше, оставаясь нерешенной еще почти полвека. При этом нельзя сказать, что все это время попытки найти заветную апериодическую моноплитку были абсолютно бесплодными. Так, в 2010 году Джошуа Соколар и Джоан Тейлор представили на суд математической общественности свою версию. Общественность, правда, отказалась признавать их моноплитку «честным» решением «задачи Эйнштейна», поскольку, в зависимости от модели, либо эта плитка не является связной (рис. 5), либо правила замощения определяются не только ее формой. Подробнее об этом можно прочитать в картинке дня Замощение Соколара — Тейлор.

Рис. 5. Один из вариантов реализации «плитки», используемый в замощении Соколара — Тейлор. Рисунок с сайта en.wikipedia.org

И вот, наконец, в марте в архиве электронных препринтов появилась статья с лаконичным названием An aperiodic monotile, в которой описан первый «честный» пример моноплитки, которой можно замостить плоскость без пробелов и наложений, и для которой все такие замощения являются исключительно непериодическими (рис. 1). За характерную форму моноплитку сразу же окрестили «шляпой». Несмотря на долгую историю задачи, «шляпа» устроена довольно просто, и даже изящно: это тринадцатиугольник, который составлен из восьми одинаковых четырехугольников, каждый из которых получается разрезанием равностороннего треугольника на три одинаковые части (рис. 6).

Рис. 6. «Шляпа» — апериодическая моноплитка. Любое замощение копиями этой плитки будет непериодическим. Рисунок © Хайдар Нурлигареев

Примечательно, что лавры открытия «шляпы» принадлежат Дэвиду Смиту (David Smith), который не является профессиональным математиком. Замощения плоскости вообще остаются одной из немногих областей математики, в которой любители делают значительные открытия с заметной регулярностью. Чего только стоит история поиска пятиугольных моноплиток! Математики-профессионалы несколько раз объявляли, что при помощи компьютера перечислили все возможные типы пятиугольников, которыми можно замостить плоскость. Однако раз за разом домохозяйка Марджори Райс обнаруживала новые формы, и ученому сообществу всякий раз приходилось поправлять свои выкладки, из-за чего вера в компьютерные доказательства на какое-то время была слегка подорвана. Возможно, такая особенность замощений вызвана тем, что их структура подчас весьма нетривиальна, и ее изучение пока далеко от завершающей стадии. Поэтому решающим фактором при поиске новых форм порой становится не знакомство со сложными теориями, во всей своей полноте доступными лишь профессионалам, а количество часов, которые любитель готов провести за прикладыванием вырезанных из бумаги многоугольников друг к другу.

Однако без профессиональных математиков в мире замощений все-таки не обойтись. Когда новая форма найдена, необходимо строго обосновать, что она обладает всеми заявленными свойствами, и в этом деле профессионалы незаменимы. В случае со «шляпой» они придумали целых два различных доказательства апериодичности. Одно этих доказательств можно назвать классическим в теории замощений: было показано, что «шляпы» организуются между собой в макроплитки определенной формы, которые образуют строгую иерархию. Поэтому, как и любое строго иерархическое замощение, каждое замощение «шляпами» является непериодическим (подробно о строгих иерархиях и самоподобных замощениях читайте в картинке дня Самоподобные замощения, в которой эта же идея проиллюстрирована другим примером).

Второе доказательство базируется на том, что замощение, изображенное на рис. 1, можно немного деформировать без потери важных для нас свойств. Имеется в виду, что, как и в исходном замощении, полученные деформацией плитки одинаковы между собой и обладают той же площадью, что и «шляпа». Таким образом, мы получаем бесконечное семейство моноплиток, замощения которыми ведут себя схожим образом (рис. 7).

Рис. 7. Деформации «шляпы». Анимация с сайта cs.uwaterloo.ca

Однако разные деформации в пределе могут дать разный результат. В нашем случае «шляпу» можно продеформировать в две различные фигуры, составленные из равносторонних треугольников: в одну из них входит четыре треугольника, а во вторую — восемь (рис. 8). Поскольку площади этих фигур равны, отсюда следует, что длины сторон входящих в них треугольников отличаются в \(\sqrt2\) раз. Соответственно, порожденные этими фигурами треугольные решетки, также изображенные на рис. 8, несоизмеримы. А это значит, что не существует параллельного переноса, который сохранял бы одновременно и первую решетку, и вторую. Таким образом, если бы существовало периодическое замощение «шляпами», то вектор параллельного переноса был бы одним и тем же для всех деформированных замощений, и в частности, для замощений фигурами, изображенными на рис. 8, но этого, как мы поняли, быть не может.

Рис. 8. Предельные формы, получающиеся в результате деформаций «шляпы». Рисунок © Хайдар Нурлигареев

Строго говоря, эти результаты пока еще не прошли формальную проверку — научное сообщество внимательно изучает корректность изложенных в препринте доказательств. Однако предварительный анализ показывает, что проблем на этапе верификации возникнуть не должно, и проверка почти наверняка будет успешно пройдена.

Замощение «шляпами» уже нашло себя в искусстве. Вот несколько примеров.

Роберт Фэтхауэр (Robert Fathauer), продолжатель традиций Маурица Корнелиса Эшера, замостил плоскость шляпами и рубашками (рис. 9).

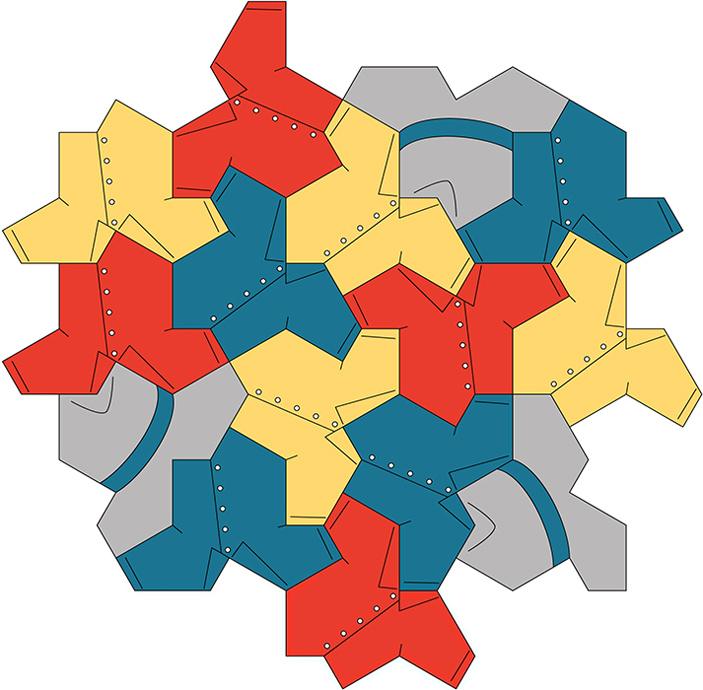
Рис. 9. Замощение плоскости «шляпами» и «рубашками». Рисунок из твиттера Роберта Фэтхауэра

Дейв Пагурек (Dave Pagurek) создал красочную анимацию, в которой масштаб замощенной области постепенно увеличивается (рис. 10).

Рис. 10. Кадр из анимации Дейва Пагурека. Рисунок с сайта openprocessing.org

А Йошиаки Араки (Yoshiaki Araki) сделал сайт, где любой желающий может создать свой собственный рисунок на любой из бесконечного множества деформированных апериодических моноплиток по своему выбору. Помимо шляпы, в качестве примеров Йошиаки приводит изображения птицы, черепахи и пингвина.

Будем надеяться, что и в других областях человеческого знания, таких как теория квазикристаллов, новые открытия и приложения не заставят себя долго ждать.

Источник: David Smith, Joseph Samuel Myers, Craig S. Kaplan, Chaim Goodman-Strauss. An aperiodic monotile // Препринт arXiv:2303.10798 [math.CO].

См. также:
1) Страничка одного из авторов обсуждаемой работы, Крейга Каплана (Craig S. Kaplan), посвященная найденной апериодической моноплитке.
2) Видео, в котором авторы рассказывают о своем открытии.

Хайдар Нурлигареев