Пятьдесят пенни

В сухом математическом остатке мы получаем такую задачу: нужно разбить число 50 на 4 слагаемых. Причём некоторые из них могут быть нулевыми, а разбиения, отличающиеся порядком слагаемых, мы считаем разными.

Давайте разложим все монеты в ряд и будем разделять части этого ряда из монет, которые причитаются разным помощникам. Понятно, что нам понадобится 3 «разделителя», чтобы разбить все монеты на 4 части. Теперь каждый способ раздать монеты четверым описывается расположением этих разделителей в ряду монет. При этом удобно считать, что разделители — это тоже элементы ряда.

Конечно, эту задачу можно решать очень по-разному, но попробуем закончить, пожалуй, самое простое решение, намеченное в подсказках. Давайте в качестве разделителей возьмём «пустые» элементы ряда или, если угодно, другие монеты, которые никому не достаются. В итоге получится ряд длины 53 из монет и разделителей. Каждое расположение разделителей описывает один вариант получения помощниками награды. Монеты слева от первого разделителя достанутся первому помощнику (то есть это будет первое слагаемое в разложении числа 50 в сумму четырёх слагаемых), между первым и вторым разделителями — второму, и так далее. Остаётся понять, сколькими способами можно расставить 3 разделителя на 53 местах. Другими словами: сколькими способами можно выбрать 3 места для разделителей из 53? А это — знакомое многим число сочетаний .

Ясно, что совершенно аналогичные рассуждения работают в случае произвольных натуральных n и k вместо чисел 50 и 4. Полученная формула —  — называется количеством разложений числа n в сумму k слагаемых. Заметим, что если забыть про проблемы Шерлока Холмса, то задача не очень-то полезная — мы зачем-то разбиваем число на слагаемые, среди которых могут быть нули, да ещё и считаем одинаковые разложения много раз.

Зададимся более логичным вопросом: сколько существует разбиений числа n на натуральные слагаемые, если разбиения, различающиеся только порядком слагаемых, считать одинаковыми? Это число p_n, оно так и называется — количество разбиений числа n. Для чисел p_n уже нет такой простой общей формулы, как для чисел разложений. Интересно, что наиболее удобная известная формула — пентагональная теорема (см. также Pentagonal number theorem) — для вычисления числа разбиений принадлежит Эйлеру. Это — рекуррентная формула, она позволяет вычислить p_n, зная значения количества разбиений для чисел, которые меньше данного n. Для читателей, знакомых с производящими функциями, доказательство этой формулы не будет чрезмерно трудным (см., например, доказательство в книге С. К. Ландо «Лекции о производящих функциях»).

К слову, для изучения разных числовых последовательностей, в том числе и обсуждаемой нами последовательности p₁, p₂, ..., p_n, ..., производящие функции — это очень мощный инструмент.

Основная идея тут такая: давайте вместо последовательности рассматривать бесконечный ряд (чтобы это ни значило!), умножая каждое p_k на x^k и складывая все эти произведения от k = 0 до бесконечности; получится такая «функция» от переменной x: 1 + p₁x + p₂x² + p₃x³ + ... Зачастую, для неё существует и другая, короткая запись. Представьте, себе, например, известную со школы геометрическую прогрессию 1 + x + x² + x³ + ... (а её можно рассматривать и как производящую функцию для последовательности 1, 1, 1, ...!). Если умножить этот бесконечный ряд на 1 − x, то получится 1 (проверьте это), поэтому можно заключить, что
1 + x + x² + x³ + ... = 1/(1 − x).

Похожие приёмы работают и в более трудных случаях. Так, производящая функция для последовательности чисел разбиений p_n равна

Много интересного про производящие функции можно узнать из уже упоминавшейся книги С. К. Ландо «Лекции о производящих функциях».

Бывает интересно считать число разбиений на фиксированное количество слагаемых или на слагаемые, каждое из которых не больше заданного числа. Здесь встречаются довольно неожиданные факты: например, число разбиений числа на различные слагаемые равно числу разбиений на нечётные слагаемые. Это утверждение довольно просто доказывается методами производящих функций.

У чисел разбиений есть наглядная геометрическая интерпретация — диаграммы Юнга (см. также Young diagram). Количество клеток в диаграмме Юнга равно n, количество строк равно количеству слагаемых, а длины строк равны самим слагаемым. Есть и другие варианты графического изображения — диаграммы Ферре (см. Ferrers diagram) и диаграммы Майя.

Диаграммы Юнга, отвечающие всем пяти возможным разбиениям числа 4 на слагаемые

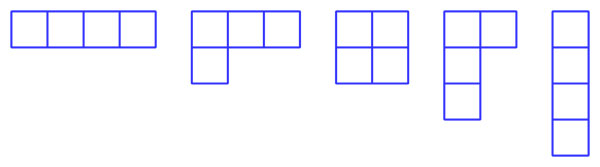
Диаграммы Юнга появляются в совершенно разных областях математики и физики. Они играют далеко не последнюю роль в теории представлений, исчислительной геометрии, теории инвариантов. Многие сложные утверждения вытекают из простых наглядных свойств диаграмм Юнга.

Отдельная интересная задача — найти количество диаграмм Юнга, помещающихся в прямоугольнике с фиксированными сторонами или с фиксированным количеством клеток, или даже трёхмерных диаграмм Юнга. Обо всём этом можно почитать в статье В. Горина «Что можно сложить из кубиков?» («Квант» №3, 2012, есть PDF номера с полным текстом статьи).