Плавление начинается с поверхности
Свойства вещества на поверхности твердого тела не такие, как в его толще. Молекулы непосредственно поверхностного слоя находятся в особых условиях, им не хватает соседей сверху. Из-за этого меняется их поведение, а через них — и свойства целого приповерхностного слоя некоторой толщины. Например, может получиться так, что при какой-то температуре само кристаллическое тело еще остается твердым, но вблизи границы уже существует жидкий приповерхностный слой (точнее, он квазижидкий, но эти тонкости тут несущественны). Чем ниже температура, чем тоньше этот слой. Но даже когда его толщина составляет всего одну молекулу, этот разупорядоченный слой всё равно кардинально отличается от упорядоченного кристалла. На рис. 1 на примере льда условно показано, как изменяется поведение поверхности кристалла с ростом температуры от абсолютного нуля и до точки плавления.

Нетрудно догадаться, почему так происходит. Каждая молекула кристалла, конечно, в среднем занимает определенный узел кристаллической решетки, но за счет ненулевой температуры она постоянно дрожит вблизи своего идеального положения. Соседние молекулы сдерживают это дрожание; молекула как бы находится в потенциальной яме, которую создают соседние молекулы. Пока температура низкая, энергия молекул мала (она обычно пропорциональна температуре), а значит, и амплитуда теплового дрожания мала, много меньше среднего расстояния между молекулами. При повышении температуры дрожание усиливается, его амплитуда растет, и когда она становится больше определенного порога (примерно 10% от межмолекулярного расстояния), молекула уже не может долго оставаться внутри этой ямы и стремится выскочить из нее. Так, в самом простом виде, начинается плавление.

Рис. 2. Простейшая модель взаимодействия в кубической кристаллической решетке: каждый выбранный атом (он выделен цветом) взаимодействует только со своими ближайшими соседями (показаны стрелками), и взаимодействие от каждого соседа создает одинаковый вклад в суммарную потенциальную яму, в которой движется выбранный атом
Понятно, что чем слабее сдерживающая потенциальная яма, тем больше амплитуда тепловых колебаний при заданной температуре. Или же, если взглянуть на ситуацию иначе, — тем ниже та температура, при которой колебания достигают критического размаха и происходит плавление. Приповерхностные молекулы чувствуют меньше соседей, поэтому они находятся в более слабой потенциальной яме, и потому плавление на поверхности начинается раньше, при более низкой температуре, чем в толще. Это явление называется предплавлением (premelting).
Всё, что сказано выше — это пока общие рассуждения. Они наверняка понятны каждому, но они не дают «ощущения масштаба». Для этого нужно перейти от качественных рассуждений к числам, получить хоть какую-нибудь оценку того, при какой температуре начинается предплавление (то есть оценить, где граница между B и C на рис. 1). Конечно, это явление довольно сложное, и вряд ли мы можем претендовать на что-то реалистичное. Но в этой задаче упор делается вовсе не на реалистичность, а именно на минимальную оценку, на первый шаг на пути от общих слов к реальной физике.
Для этого построим простейшую модель явления. Во-первых, для простоты возьмем обычную кубическую кристаллическую решетку, состоящую из отдельных атомов одного сорта (рис. 2). Во-вторых, будем считать, что каждый атом чувствует потенциальную яму, которая есть просто сумма потенциальных ям, создаваемых для него каждым ближайшим атомом-соседом. В-третьих, опять же для максимальной простоты будем считать, что потенциальные ямы от всех ближайших соседей одинаковы и сферически симметричны. Мы уже договорились считать, что плавление наступает тогда, когда амплитуда колебаний атомов превышает некоторый фиксированный порог.
Задача
Найдите, при какой температуре наступит предплавление в поверхностном слое в этой модели, если температура плавления в объеме равна T0. Оцените эту температуру для льда.
Подсказка
Мы хотим сравнить температуры плавления T (на поверхности) и T0 (в объеме) — или же пропорциональные им энергии молекул E и E0, которые отвечают ровно таким колебаниям, у которых амплитуды равны некоторому фиксированному значению (это и есть критерий плавления). Поэтому нам нужно сравнить два графика потенциальной энергии — для атомов внутри объема и для атомов на поверхности, — и выяснить, как соотносятся друг с другом эти критические энергии или соответствующие им температуры. Остается только понять, сколько у каждого атома соседей (не забываем, что, в отличие от картинки, кристалл трехмерный!) и как связаны друг с другом эти два графика.
Решение
Пусть V(x) — график потенциальной энергии выбранного атома (x — его координаты), возникающей за счет взаимодействия с одним ближайшим соседом (рис. 3, слева). Тогда если таких соседей N, полная потенциальная энергия, ощущаемая атомом, есть просто N·V(x). В этой простейшей модели каждый атом в глубине имеет шесть ближайших соседей, а атом, лежащий на поверхности, — пять. Графики потенциальной энергии на поверхности, 5V(x) (рис. 3, в центре) и в толще кристалла, 6V(x) (рис. 3, справа) будут тогда одинаковыми по форме, но только «поверхностный» график будет составлять 5/6 от «объемного». Этот вывод не зависит от формы потенциальной ямы.

Рис. 3. Профиль потенциальной энергии, ощущаемой выбранным атомом. Слева: за счет только одного соседа; в центре: за счет пяти соседей (поверхностный атом); справа: за счет шести соседей (атом в глубине кристалла). E и E0 — энергии, которые должны иметь атомы для того, чтобы их колебания в этом потенциале имели критическую амплитуду
Поскольку форма графиков идентична, то и колебания одинакового размаха в таких потенциальных ямах будут отвечать энергиям E и E0, которые тоже связаны множителем 5/6. А раз энергия пропорциональна температуре, то получаем искомое соотношение между температурами плавления: T/T0 = 5/6. Для льда T0 составляет 273 К, поэтому T получится 227 К, то есть примерно –45°C. В рамках нашей модели получается, что предплавление начинается при таких жгучих морозах.
Послесловие
Первым делом надо четко сказать, что наша модель, безусловно, очень упрощенная и даже искусственная. Она не учитывает ни реальный вид решетки, ни реальное взаимодействие молекул, ни квантовых эффектов, ни блуждание молекул сверху поверхности, ни то, как потеря кристаллического порядка проникает вглубь кристалла. Но она ничего этого и не должна была учитывать. Главная задача этой модели — преодолеть страх, который возникает у многих людей, интересующихся современной физикой, когда им предлагают перейти от словесных описаний к минимальным вычислениям. Обычно считается, что любой вопрос про современную физику будет обязательно очень сложным, и разобраться с ним «простому гражданину» нереально. Вовсе нет! — многие численные оценки по порядку величины можно делать самому. Согласитесь, у этой задачи короткое решение и понятный ответ; он моментально превращает общие словесные рассуждения в четко осязаемое число. Это решение не требует никаких сложных формул, не использует никакие сокровенные знания из физики, оно вполне по силам человеку, который внимательно прочтет вступление и подумает над предложенной моделью. Надо просто не бояться делать таких попыток.
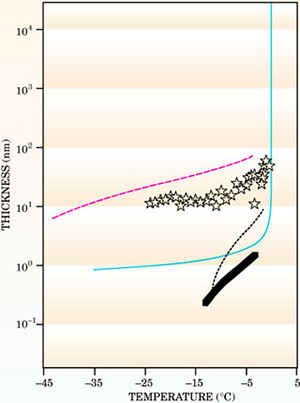
Рис. 4. Компиляция экспериментальных данных по измерению толщины квазижидкого слоя (в нанометрах) в зависимости от температуры. Все точки и линии показывают экспериментальные данные разных групп. Phys. Today 56, 50 (2005)
Возвращаясь к физике, заметим, что полученный нами ответ может показаться слишком экстремальным. На основе повседневного опыта человек обычно готов допустить, что какое-то предплавление может происходить при температурах порядка –1°C или около того. Но уж в морозилке-то (–18°C) никакого плавления не должно быть, разве не так? Опасность упования на повседневный опыт состоит в том, что мы можем непосредственно пощупать только то, что происходит с приповерхностным слоем толщиной в десятки и сотни микрон. Но в задаче речь идет про одноатомный слой! И потому, когда квазижидким остается только этот слой, повседневный опыт нам ничем не поможет, мы предплавление просто не заметим, для этого нужны тонкие методы экспериментальной физики.
Поскольку изучение льда представляет огромную ценность (как чисто научную, так и прикладную), были проведены многочисленные исследования того, что же действительно происходит на поверхности льда при понижении температуры. Самые первые опыты, косвенно демонстрирующие наличие квазижидкого поверхностного слоя, ставил еще Майкл Фарадей в 1850-е годы. Правда, его интерпретация экспериментов встретила жесткие возражения коллег, поэтому в течение целого столетия этот вопрос оставался в тени. К нему физики всерьез вернулись только во второй половине XX века, и самыми разными методами доказали наличие этого слоя и изучили разнообразные его характеристики. Состояние этой науки на конец 1970-х годов отражено в прекрасной научно-популярной книжке японского физика Н. Маэно «Наука о льде», переведенной в 1988 году на русский язык.
Правда, по мере накопления данных ситуация с экспериментальными результатами, казалось, только запутывается. Например, разные методики измерения толщины слоя в зависимости от температуры давали результаты, порой отличающиеся друг от друга на целый порядок (рис. 4). Но для нас важно одно: все эти эксперименты действительно видят тончайший водный слой вплоть до температур, сравнимых с той, что мы получили в рамках простейшей модели. Так что найденный ответ оказался не так уж и далек от истины!
Что касается данных, то спустя какое-то время было понято, что все эксперименты проводились в разных условиях (вакуум или атмосфера, наличие водяных паров или сухой воздух), а кроме того, на толщину квазижидкого слоя сильно влияли даже небольшие примеси посторонних веществ, растворенных во льду. Поэтому корректного сравнения пока достичь не удается, но в будущем такое «воссоединение методик» нужно будет провести.
Если же обратить внимание именно на самый-самый поверхностный слой молекул в кристалле льда, то здесь самые аккуратные данные были получены в 2001 году (статья в журнале Phys.Rev.Lett., новость на scientific.ru). С помощью спектроскопического и поляризационного анализа авторы смогли выделить сигнал от «торчащих наружу» OH-связей и измерили их ориентационную упорядоченность. Результаты (см. рис. 5) показали, что постепенная потеря упорядоченности начинается аж при –70°C! Кстати, результаты численного моделирования поведения микрокусочка льда методом молекулярной динамики тоже дают примерно такие числа.

Рис. 5. Ориентационные свойства свободных OH-связей на поверхности льда в зависимости от температуры. Черные точки (шкала слева) показывают ориентационный порядок (1 — идеальный порядок, 0 — полный беспорядок), белые точки (шкала справа) показывают средний угол наклона OH-связей относительно перпендикуляра к поверхности. Изображение из статьи PRL 86, 1554 (2001)
Ну и напоследок скажем, что мы только по верхам коснулись одной лишь темы в этом большом разделе физики. Более подробно о структуре поверхности льда, а также о геофизических, климатических, астрофизических и повседневных последствиях этой структуры можно узнать из упомянутой уже книжки Н. Маэно «Наука о льде», а также англоязычных статей: R. Rosenberg. Why Is Ice Slippery? // Physics Today 56, 50 (2005) и J. G. Dash, A. W. Rempel, J. S. Wettlaufer. The physics of premelted ice and its geophysical consequences // Reviews of Modern Physics 78, 695–741 (2006).
-
Ещё подумал. И плавится кристалл должен по-вашему не при температуре объёмного плавления, а при температуре поверхностного плавления, когда поверхностный слой кристалла превращается в жидкость, а вслед за этим в жидкость превращается следующий атомарный слой и т.д.
Возможно данную задачу чуть проще рассматривать для модели Ленца-Изинга, где есть определённая константа связи, а не предполагаемый потенциал. Так вот. Фазовый переход в этой задаче - коллективный эффект, который имеет место при определённой температуре во всём теле (даже при его конечных размерах), а не отдельно в разных частях.
Последние задачи














Рис. 1. Схематичное изображение того, что происходит с поверхностью кристалла льда при повышении температуры от абсолютного нуля до температуры плавления. (A) тепловые колебания не нарушают структуру решетки; (B) в поверхностном слое начинают появляться дефекты, но структура в целом держится; (C) поверхностный слой теряет порядок, начинается предплавление; (D) предплавление простирается всё дальше вглубь кристалла, образуется жидкий приповерхностный слой, лед становится скользким; (E) вода. Адаптированное изображение из статьи J. Phys. Chem. C 111, 9631 (2007)