Как украсить елку?

Попробуйте выяснить при каких малых n задача имеет решения, а при каких — нет. Подумайте, с какими из этих случаев можно сопоставить решение для n = 2025.

Сначала надо убедиться, что при \(n=2025\) елка содержит кратное трем число шестиугольников, потому что игрушка состоит из трех шестиугольников. В самом деле, в елке \(1+2+\ldots+n=\frac12n(n+1)\) шестиугольников, поэтому при \(n=2025\) получим число, кратное 3, ведь 2025 делится на 3. То есть необходимое условие выполнено.

Покажем, что при \(n=2025\) елку можно украсить. Отметим два действия с елками, которые пригодятся при решении задачи:
    Д1: к елке, у которой \(n\) шестиугольников на стороне, где \(n\) — нечетное, можно добавить три слоя шестиугольников — желтую «трапецию» на рис. 2, — которую можно украсить игрушками. При этом получим новую елку, на стороне которой \(n+3\) шестиугольника, при этом число \(n+3\) — четное.

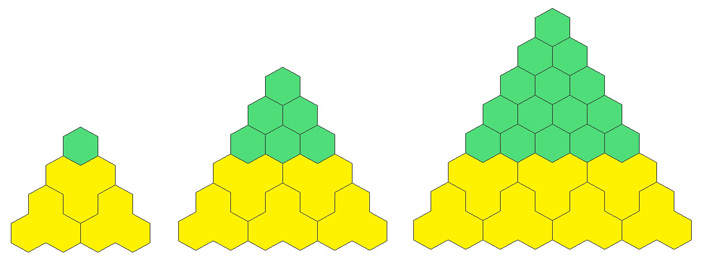
Рис. 2.

    Д2: елку с четным числом \(n\) шестиугольников на стороне можно окружить по периметру синим «треугольным кольцом» в три слоя шестиугольников, которое можно украсить игрушками (рис. 3). При этом получим новую елку, на стороне которой \(n+9\) шестиугольников, и при этом число \(n+9\) — нечетное.

Рис. 3.

Это значит, что если к елке, на стороне которой \(n\) шестиугольников, поочередно применить действия Д1 и Д2 в нужном порядке в зависимости от четности числа \(n\), то размер елки увеличится на \(3+9=12\) шестиугольников.

Для елки с \(n=2025\) нужно выяснить, какого размера будет наименьшая зеленая «сердцевина». Очевидно, размер внутренней елки будет равен остатку от деления 2025 на 12. Поскольку \(2025 = 12\cdot168+9\), размер внутренней елки равен 9, то есть на ее стороне 9 шестиугольников. Но елку размера \(n=9\) можно украсить игрушками, это показано на рис. 4.

Рис. 4.

Применив к этой елке комбинацию действий Д1 и Д2 168 раз и учитывая, что елку размера 9 можно украсить, получим украшенную елку для \(n=2025\).

Понятно, что такую большую елку не нарисовать, поэтому на рис. 5 показана елка размера 33, которая имеет ту же «природу», потому что \(33=12\cdot3+9\).

Рис. 5.

Попробуем решить задачу в общем виде и выясним, при каких значениях \(n\) можно украсить елку. Елку, содержащую \(n\) слоев шестиугольников, будем обозначать \(E(n)\). Любое натуральное число можно представить в виде \(n=12k+r\), где \(0\le r\le 11\) — остаток от деления \(n\) на 12. Это позволяет разбить множество натуральных чисел на 12 классов: в каждом классе находятся числа, имеющие одинаковый остаток при делении на 12.

Во-первых, по условию задачи игрушка содержит три шестиугольника, поэтому можно украсить только те елки, у которых число шестиугольников кратно 3. Елка \(E(n)\) содержит \(\frac12n(n+1)\) шестиугольников, значит, число \(\frac12n(n+1)\), должно делиться на 3. Поэтому, если \(r = 1,\ 4,\ 7,\ 10\), то елку \(E(12k+r)\) точно нельзя украсить, так как число \(\frac12n(n+1)\) не делится на 3.

Выясним, при каких из оставшихся значений \(n<12\) можно украсить елку \(E(n)\). При решении основной задачи был разобран случай \(n=9\). Также можно заметить, что игрушка сама является елкой для \(n=2\). Вспомнив свойство Д2, сформулированное в решении, легко нарядить елку \(E(11)\). Поскольку нас интересуют остатки при делении на 12, то сюда же можно добавить елку-точку \(E(0)\). Все эти четыре елки приведены на рис. 6.

Рис. 6.

Отмеченные в решении задачи действия Д1 (добавить «трапецию» высотой в три шестиугольника) и Д2 (окружить елку по периметру «треугольным кольцом» в три слоя шестиугольников) позволяют каждую елку увеличить на \(3 + 9 = 12\), а если проделать эти два действия \(k\) раз, то елка увеличится на \(12k\) слоев. При этом важен порядок применения этих свойств в зависимости от четности числа \(n\).

Покажем это в каждом случае:

• \(n=0\) — четное, значит, выбранную точку надо окружить «треугольным кольцом», затем к полученной елке нужно добавить «трапецию». В результате получим елку \(E(12)\). Повторив еще раз действия Д2 и Д1 получим елку \(E(24)\) (рис. 7). Проделав действия Д2 и Д1 \(k\) раз, получим елку \(E(12k)\).

Рис. 7.

• \(n=2\) — тоже четное, значит, начинаем с елки-игрушки \(E(2)\), и надо выполнить действия Д2 и Д1 в том же порядке: окружить «треугольным кольцом», затем к полученной елке нужно добавить «трапецию». В итоге получим елку \(E(14)\) (рис. 8). Повторив еще раз действия Д2 и Д1 получим елку \(E(26)\). Проделав действия Д2 и Д1 \(k\) раз, получим елку \(E(12k+2)\).

Рис. 8.

• \(n=9\) — алгоритм построения описан в решении. Проделав действия Д1 и Д2 \(k\) раз, получим елку \(E(12k+9)\).
• наконец, \(n=11\) — тоже нечетное, значит, исходим от елки \(E(11)\), и надо выполнить действия Д1 и Д2 именно в таком порядке: добавить «трапецию», затем полученную елку нужно окружить «треугольным кольцом», получим елку \(E(23)\) (рис. 9). Повторив еще раз действия Д1 и Д2 получим елку \(E(35)\). Проделав действия Д1 и Д2 \(k\) раз, получим елку \(E(12k+11)\).

Рис. 9.

Итак, если \(r=0,\ 2,\ 9,\ 11\), то елку \(E(12k+r)\) можно украсить.

Остается открытым вопрос: можно ли украсить елку \(E(12k+r)\), если \(r=3,\ 5,\ 6,\ 8\). Здесь, к сожалению, трюк с рассмотрением самых маленьких елок не работает, поскольку их украсить точно нельзя. Возможно, читатели помогут ответить на этот вопрос.

С 1990 года проводится самая массовая и престижная московская олимпиада по математике для учеников шестых и седьмых классов — Математический праздник. Олимпиада проходит ежегодно в одно из февральских воскресений в главном корпусе МГУ. На одном из «Матпраздников» шестиклассникам была предложена задача нашей тематики:

Рис. 10.

Равносторонний треугольник со стороной 8 разделили на равносторонние треугольнички со стороной 1 (рис. 10). Какое наименьшее количество треугольничков надо закрасить, чтобы все точки пересечения линий (в том числе и те, что по краям) были вершинами хотя бы одного закрашенного треугольничка? Приведите пример и докажите, что меньшее количество треугольничков закрасить нельзя.

Чтобы сэкономить время на олимпиаде, школьникам предлагался лист с нарисованной треугольной сеткой.

Ответ и комментарий

Рис. 11.

Ответ в этой задаче: 15 треугольничков. Пример приведен на рис. 11.

Оценка совсем проста: заметим, что в этом примере закрашенные треугольнички не имеют общих вершин, то есть каждая точка пересечения линий является вершиной ровно одного из них. Это значит, что меньшего числа треугольничков не хватит.

На первый взгляд — это задача на раскраску, но если сравнить с рис. 4, то можно понять, это эквивалентные задачи.

Вот еще одна задача, которая перекликается с нашей:

Рис. 12.

Точечный треугольник — это множество узлов правильной треугольной решетки, расположенных в форме правильного треугольника (пример показан на рис. 12). Три вершины правильного единичного треугольника назовем тройкой. Можно ли все точки точечного треугольника, на каждой стороне которого лежит 2018 точек, разбить на непересекающиеся тройки?

Украшают елки и на Международной математической олимпиаде (хотя, вероятно, авторы задачи не подозревали об этом). Например, в 2023 году на 64 ММО в Японии участникам предлагалась задача:

Рис. 13.

Пусть \(n\ge1\) — натуральное число. Японский треугольник состоит из \(1+2+\ldots+n\) одинаковых кругов, выложенных в форме равностороннего треугольника так, что для каждого \(i=1,\ 2,\ \ldots,\ n\) ряд с номером \(i\) состоит ровно из \(i\) кругов, в точности один из которых покрашен в красный цвет. Путем ниндзя в японском треугольнике называется последовательность из \(n\) кругов, построенная следующим образом: начинаем с круга в ряде 1, а затем поочередно спускаемся вниз, переходя от круга к одному из двух кругов непосредственно под ним, пока не дойдем до нижнего ряда. На рис. 13 приведен пример японского треугольника для \(n=6\), а также пути ниндзя, содержащего два красных круга. Найдите наибольшее число \(k\) (зависящее от \(n\)) такое, что в любом японском треугольнике существует путь ниндзя, содержащий хотя бы \(k\) красных кругов.

Попробуйте решить эту задачу и окунитесь в атмосферу Международной математической олимпиады, почувствуйте уровень ее сложности. И если вам удастся решить задачу, то ответом вы точно удивитесь.

С наступающим Новым годом!