Квадрат в синусе

Постройте математическую модель задачи, составив соответствующее уравнение. На вид оно должно получиться довольно громоздким, но это не должно вас испугать: чтобы ответить на поставленные в задаче вопросы, решать его не потребуется. Нужно будет проанализировать это уравнение на предмет количества корней, а сделать это удобно при помощи графиков.

Рассмотрим синусоиду \(y=n\sin x\) и квадрат \(ABCD\) на ней. Пусть вершина \(А\) имеет координаты \(A(x;\ n\sin x)\). Тогда вершина \(B\) имеет координаты \(B(n\sin x;\ -x)\), потому что получается из вершины \(А\) поворотом на 90° вокруг начала координат. Поскольку вершина \(B\) тоже лежит на этой синусоиде, то верно равенство: \(-x=n\sin(n\sin x)\). Нам нужно выяснить, сколько корней имеет это уравнение при указанных в задаче значениях \(n\).

Громоздкость полученного уравнения наводит на мысль применения графического способа решения уравнений, ведь нам нужны не корни уравнения, а их количество. Чтобы легче было строить графики, запишем уравнение в виде \(n\sin x=-\mathrm{arcsin}\,(\frac xn)\). При таком подходе нам нужно построить в координатной плоскости графики функций \(y=n\sin x\) и \(y=-\mathrm{arcsin}\,(\frac xn)\).

Первый из них хорошо известен, он представляет собой синусоиду \(y=\sin x\), растянутую вдоль оси \(Oy\) в \(n\) раз.

Чтобы понять, что представляет собой второй график, вспомним общую теорию преобразования графиков. Конкретнее, нам нужно понимать, как располагаются графики следующих трех функций друг относительно друга: некой функции \(y=f(x)\), обратной ей функции \(y=f^{-1}(x)\) и функции \(y=-f^{-1}(x)\). Из школьного курса алгебры известно, что графики \(y=f(x)\) и \(y=f^{-1}(x)\) симметричны относительно прямой \(y=x\), а графики \(y=f^{-1}(x)\) и \(y=-f^{-1}(x)\) симметричны относительно оси \(Ox\) (рис. 2).

Рис. 2.

Далее нужно вспомнить, что композицией двух осевых симметрий с пересекающимися осями на плоскости является поворот с центром в точке пересечения этих осей (см. Теорема Шаля). При этом угол поворота равен удвоенному углу между осями. В нашем случае угол между осями симметрии равен 45°, поэтому график функции \(y=-f^{-1}(x)\) получается из графика функции \(y=f(x)\) поворотом на угол 90° по часовой стрелке вокруг начала координат.

Эти рассуждения проведены для графиков функций, они же остаются в силе и для графиков уравнений, с той лишь разницей, что обратная функция не всегда существует. Дело в том, что обратная функция существует только для монотонных функций, но все рассуждения о преобразовании графиков можно провести по-отдельности для промежутков монотонности функций, входящих в уравнения: для каждого из них будет получаться одинаковый вывод о том, на какой угол и относительно какой точки нужно повернуть соответствующий кусок графика уравнения. А значит, можно считать, что он поворачивается как единое целое.

Несложно убедиться, что функция \(y=-\mathrm{arcsin}\,(\frac xn)\) — это как раз \(-f^{-1}(x)\) для \(f(x)=n\sin x\). Значит, графиком уравнения \(y=-\mathrm{arcsin}\,(\frac xn)\) является синусоида \(y=n\sin x\), повернутая на 90° вокруг начала координат.

Теперь приступим к решению конкретных задач.

1) Построим синусоиду \(y=3\sin x\) и повернем ее на 90° вокруг начала координат по часовой стрелке. Полученные два графика имеют только одну общую точку — начало координат (рис. 3). Это так, поскольку \(3<\pi\), из-за чего синусоида \(y=3\sin x\), имеющая максимум 3, заведомо не дотягивается до самого нижнего из участков повернутой линии в первом квадранте, — ведь он целиком лежит выше прямой \(y=\pi\) (из-за симметрии картинки достаточно разобраться только с первым квадрантом). Итак, в этом случае наше уравнение имеет единственный корень \(x=0\), что соответствует вырожденному квадрату со стороной 0. Поэтому при \(n=3\) на синусоиде нет квадратов.

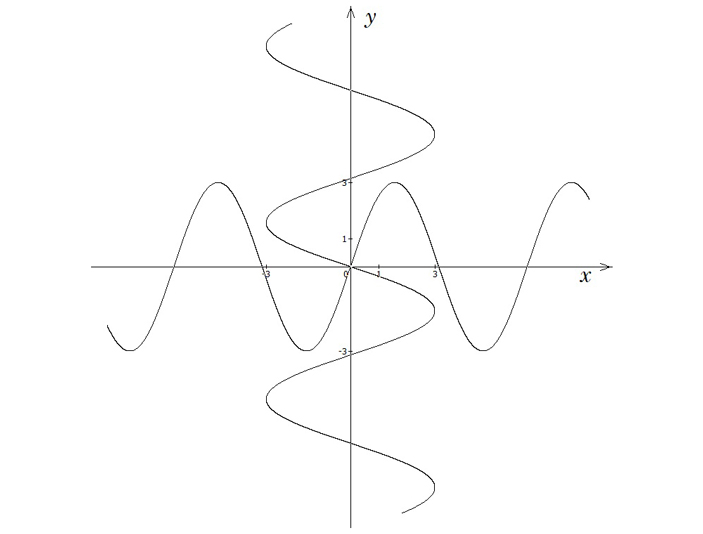
Рис. 3.

В дальнейшем тривиальный корень \(x=0\) не будет для нас представлять интереса.

2) Построим синусоиду \(y=5\sin x\) и повернутую синусоиду \(x=-5\sin y\). Эти два графика пересекаются в 9 точках, восемь из которых являются вершинами двух квадратов (рис. 4).

Рис. 4.

3) Чтобы определить количество квадратов, вершины которых лежат на синусоиде \(y=10\sin x\), можно поступить так же, как и до этого: построить два графика и отметить их точки пересечения. Заметим, что у каждого квадрата по одной вершине лежит в каждой координатной четверти, поэтому, в принципе, можно построить фрагменты графиков в одном квадранте. Но если нарисовать графики полностью, то получится 41 точка пересечения (рис. 5). Начало координат не является вершиной квадрата, значит, существует всего 10 различных квадратов, все вершины которых лежат на синусоиде \(y=10\sin x\).

Рис. 5.

Естественный вопрос: а сколько квадратов лежит на синусоиде \(y=n\sin x\) при других натуральных значениях \(n\)? Пользуясь методом, рассмотренным при решении основной задачи, можно найти число \(a(n)\) квадратов при не очень больших \(n\), то есть, фактически, определить начало последовательности \(a(n)\). Вот ее первые двадцать членов:

Решая задачу графически, мы отметили, что у каждого искомого квадрата по одной вершине лежит в каждой координатной четверти, поэтому можно построить фрагменты графиков \(y=n\sin x\) и \(y=-\mathrm{arcsin}\,(\frac xn)\), расположенные только в этой четверти, и посчитать точки пересечения — именно столько будет квадратов. На рис. 6 показан такой фрагмент пересечения графиков при \(n=18\), и отмечены точки пересечения. Но чтобы рассмотреть участок, помеченный знаком вопроса, нужно уметь увеличивать картинку. Это, да и вообще вручную пересчитывать точки, не очень удобно.

Рис. 6.

Тем не менее, кое-какие наблюдения можно сделать и в «ручном» режиме. Интересно, что во всех таких «спорных» ситуациях, когда синусоиды проходят очень близко, точек пересечения либо две, либо ноль. Ровно одна точка пересечения не обнаруживалась ни разу, то есть касание синусоид не получалось. Бывает ли касание синусоид при натуральных \(n\)? Этот вопрос пока остается открытым.

С увеличением \(n\) квадраты, если изобразить только их, выстраиваются в симпатичный узор. Так, на синусоиде \(y=20\sin x\) расположено 42 квадрата, а на синусоиде \(y=50\sin x\) — 252 квадрата. Соответствующие «паутины» изображены на рис. 7.

Рис. 7.

По таблице можно построить график начального участка последовательности \(a(n)\). Он представляет собой множество из 20 точек, абсциссы которых — это номера членов последовательности, ординаты — члены последовательности (рис. 8). Например, буквой \(A\) на рис. 8 отмечен 13-й член последовательности, равный 18.

Рис. 8.

Интересно, что график последовательности хорошо согласуется с параболой \(y=\frac{n^2}{\pi^2}\): точки графика располагаются в непосредственной близости от параболы. Это означает, что члены последовательности можно приблизительно находить по формуле \(a(n)\approx\frac{n^2}{\pi^2}\). Почему это так, станет понятно чуть ниже.

Как следует из того, что мы уже обсуждали, число \(a(n)\) связано с количеством решений \(K_n\) уравнения \(n\sin (n\sin x)=-x\) равенством \(a(n)=\frac{K_n-1}{4}\). Эта формула очевидна, но толку от нее мало, потому что в общем случае непонятно, как решать это тригонометрическое уравнение.

Несмотря на то, что информации о последовательности было не очень много, я отправил ее в Энциклопедию целочисленных последовательностей (OEIS) Нила Слоуна. В течение месяца эксперты OIES ее изучали, но в конечном итоге она была одобрена и теперь находится в Энциклопедии под номером A345256. Мне особо приятно, что это сделал сам Нил Слоун. Теперь любители математики со всего мира могут пополнять информацию об этой последовательности. Так, сначала она была продолжена Цзиньюанем Ваном до 61-го члена, затем Димитаром Цветковым — до 237-го члена. Но настоящий прорыв совершил Мераб Левиашвили, который нашел и обосновал формулу \(n\)-го члена последовательности:

где квадратными скобками обозначено взятие целой части.

Найденная формула пугающе громоздка, но она позволяет найти \(a(n)\) для любого \(n\). Также из нее видно, откуда берется близость к параболе \(y=\frac{n^2}{\pi^2}\). Правда, здесь хотелось бы получить и какое-то другое обоснование. Тальмон Сильвер, пользуясь этой формулой, вычислил 1000 первых членов последовательности. Удивительно, но все они четные — значит, касания синусоид по-прежнему нет. Можно ли доказать, что оно невозможно?

Есть еще одно интересное наблюдение, связанное с нашими синусоидами, которым поделился Владимир Данилов. Оно пока не доказано, но проверено для небольших \(n\). Оказывается, если синусоиду заменить зигзагообразной ломаной, вершинами которой являются точки экстремумов синусоиды (рис. 9), то, применяя графический метод решения задачи, будем получать ту же последовательность \(a(n)\): число квадратов на синусоиде совпадает с числом квадратов на ломаной.

Рис. 9.

Как мы уже обсуждали, пока непонятно, возможно ли касание синусоид (и, как следствие, нечетное число квадратов) при натуральных \(n\). Но что, если отказаться от требования \(n\in \mathbb{N}\)?

Поскольку на синусоидах \(y=n\sin x\) при n = 1, 2 и 3 нет ни одного квадрата, а при n = 4 их уже два, то из соображений непрерывности ясно, что при каком-то значении \(n\) между 3 и 4 на синусоиде \(y=n\sin x\) должен оказаться только один квадрат. Это значение можно найти при помощи компьютера, оно равно 3,582214964954015... Лежащая в первой четверти вершина квадрата имеет абсциссу 1,485057422744014... Интуиция подсказывает, что это значение является иррациональным числом. На рис. 10 изображены соответствующие касающиеся синусоиды и единственный лежащий на них квадрат.

Рис. 10.